5.2.1.Передаточное отношение

Передаточным отношением зубчатого механизма называется отношение угловых скоростей w ведущего колеса w_j и ведомого w_k. Если j – ведущее колесо, а k – ведомое, то

Если движение передается от k-го колеса к j-ому, то

Если угловая скорость ведущего колеса больше, чем угловая скорость ведомого (U>1), то такой механизм называется редуктором; в противном случае – мультипликатором.

На кинематических схемах зубчатые колеса принято изображать в виде окружностей, которые касаются друг друга. Эти окружности называют начальными.

Одноступенчатые зубчатые механизмы состоят из двух колес и стойки (рис. 5.9–5.12).

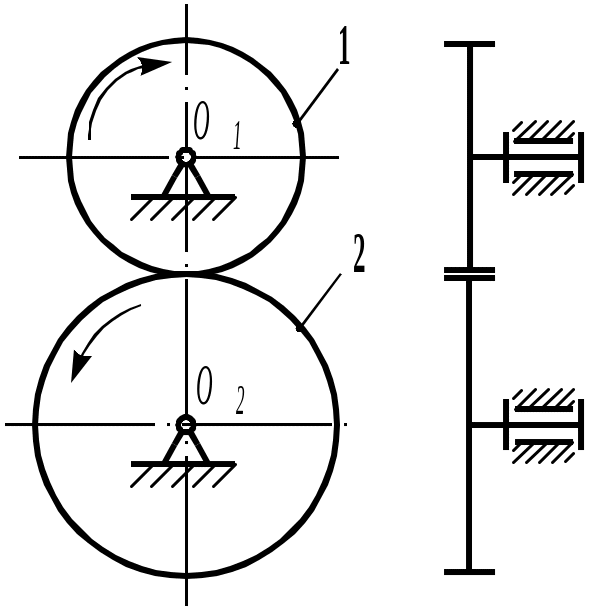
Рис. 5.108 .Трехзвенная зубчатая передача с внешним зацеплением

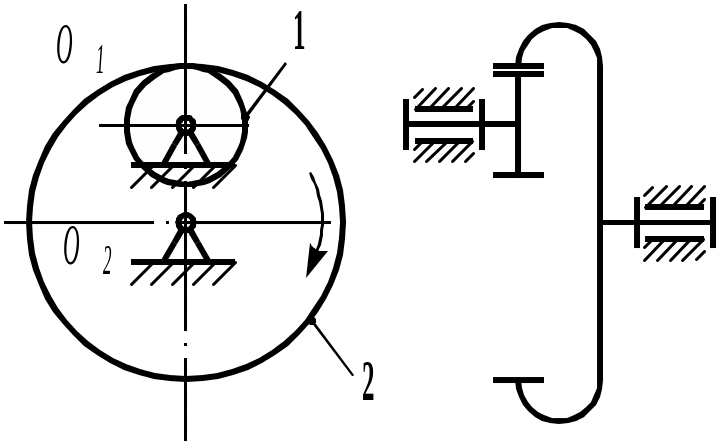
Рис. 5.109. Трехзвенная зубчатая передача с внутренним зацеплением

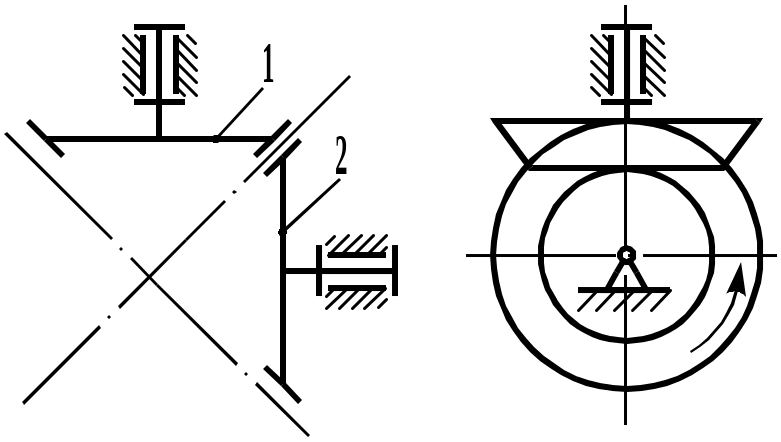
Рис. 5.110. Трехзвенная зубчатая передача с коническими колесами

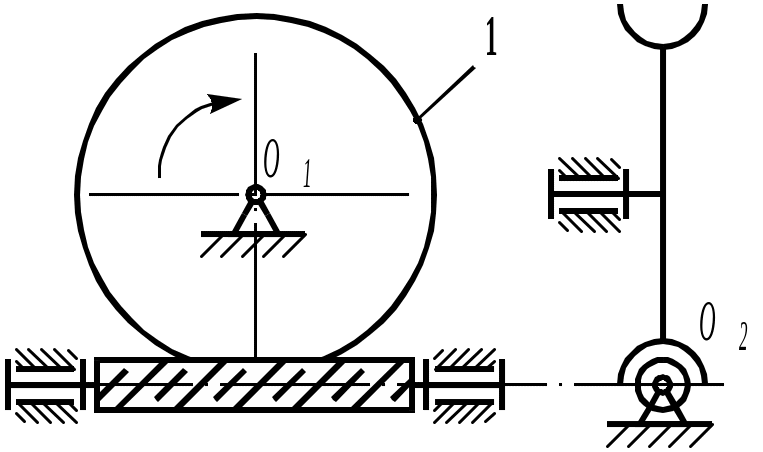
Рис. 5.111. Трехзвенная червячная передача

Передаточное отношение может быть выражено через другие параметры колес:

,

где Z_k, Z_j – числа зубьев k и j колес соответственно.

Знак плюс ставится, если колеса вращаются в одном направлении (внутреннее зацепление), в противном случае – минус (внешнее зацепление).

Передаточное отношение одноступенчатой червячной передачи при ведущем червяке (под Z следует понимать число заходов червяка) определяется по предыдущей формуле. Направление вращения ведомого звена следует определять по правилу винта и гайки.

Число заходов червяка определяется подсчетом количества витков резьбы на его торце.

Для механизмов, имеющих кроме ведомого и ведущего еще несколько промежуточных колес (Рис. 5 .112), передаточное отношение от ведущего (первого) к ведомому (n-му) колесу определяется формулой

,

где k – число пар колес внешнего зацепления.

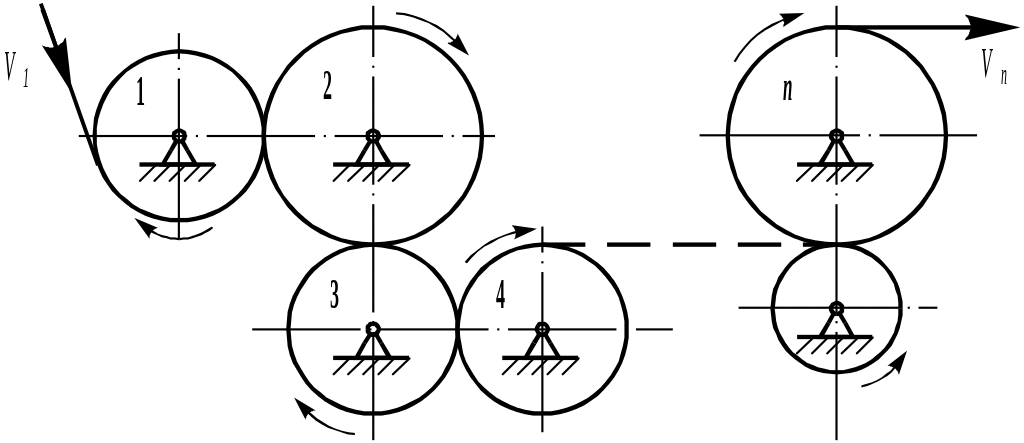
Рис. 5.112

Такой ряд колес применяется для передачи движения между валами, находящимися на большом удалении друг от друга или при необходимости воспроизведения передаточного отношения определенного знака.

Для получения большого передаточного отношения применяется ступенчатый ряд колес, в котором, в отличие от последовательного ряда колес, колеса жестко соединены между собой осью и представляют собой одно звено (Рис. 5 .113). В этом случае передаточное отношение равно произведению передаточных отношений отдельных ступеней:

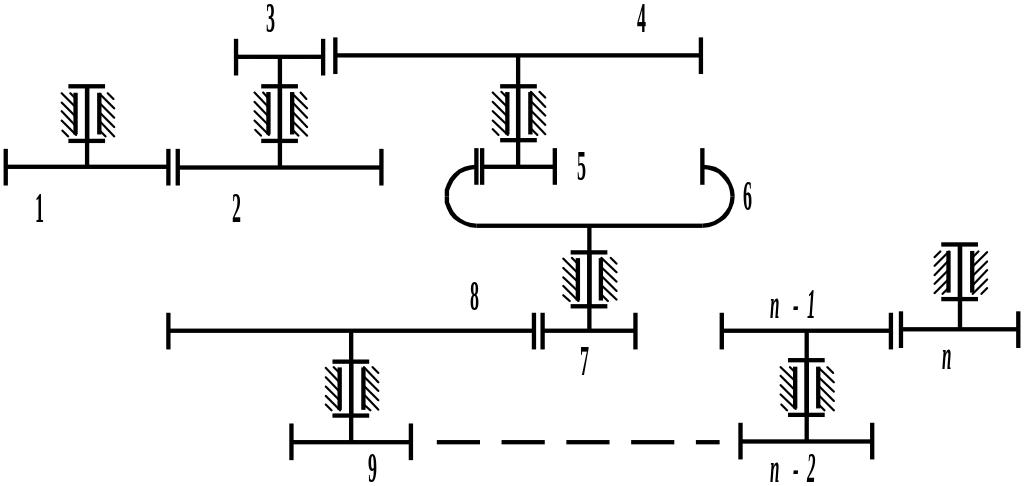
Рис. 5.113

Опытным путем передаточное отношение любой зубчатой передачи от колеса 1 к колесу n определяется поворотом входного колеса на 360 и замером угла поворота выходного звена, тогда

Знак определяется во направленно вращения выходного звена.

5.3.Планетарные и дифференциальные механизмы

Отличительная особенность планетарных и дифференциальных механизмов – наличие зубчатых колес с подвижной осью вращения. На Рис. 5 .114 изображен планетарный механизм. У него колесо 4 неподвижно, общая ось колес 2 и 2 вращается вместе с водилом Н вокруг колес 1 и 4, называемых солнечными. Колеса 2 и 2 называются сателлитами, а механизм – планетарным по аналогии с солнечной системой, в которой планеты, совершая оборот вокруг Солнца, вращаются также вокруг собственной оси.

У планетарного механизма степень подвижности равна единице. Если освободить колесо 4, то мы получим дифференциальный механизм, имеющий две степени свободы.

Для определения передаточного отношения планетарных механизмов применяется метод инверсии. В данном случае этот метод эквивалентен закреплению водила и освобождению неподвижного колеса.

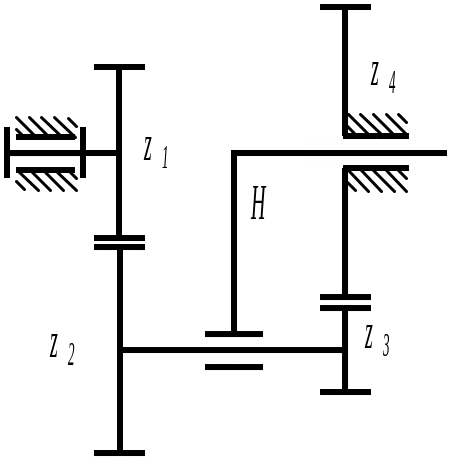
Рис. 5.114

При этом мы получаем зубчатую передачу с неподвижными осями, передаточное отношение которой может быть определено по методике, изложенной в предыдущем параграфе. На Рис. 5 .115 представлена схема механизма в обращенном движении. Передаточное отношение планетарного механизма обозначается буквой U, где верхний индекс указывает на неподвижное звено, а нижний индекс указывает номера входного и выходного звеньев. Для механизма на Рис. 5 .116, имеющего в качестве входного звена колесо 1, в качестве выходного водило Н, при закрепленном колесе 4. Передаточное отношение обозначается , а для обращенного механизма – .

Передаточное отношение рассматриваемого планетарного механизма определяется по формуле Виллиса

,

где ,

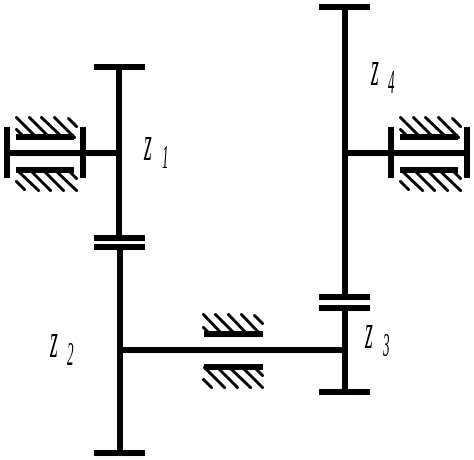
Рис. 5.115

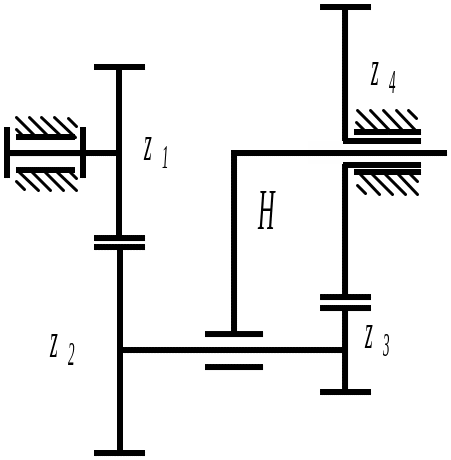
Рис. 5.116

В общем случае передаточное отношение от i-го колеса планетарного механизма к водилу при неподвижном j-ом колесе определяется формулой

.

Передаточное отношение дифференциального механизма (рис. 5.14 определяется из формулы передаточного отношения обращенного механизма

,

из которой следует, что дифференциальный механизм не имеет определенного передаточного отношения, если одно входное звено имеет определенную угловую скорость. Только при заданной угловой скорости двух входных звеньев (например, 1 и Н) передаточное отношение становится определенным.