4.4.Синтез четырехзвенных механизмов с низшими парами
4.4.1.Постановка задачи синтеза передаточного шарнирного четырехзвенника
Передаточными механизмами называются механизмы, осуществляющие заданное преобразование движений входных звеньев в движения выходных звеньев. Такие механизмы широко распространены в технике.
В синтезе передаточных механизмов используются все рассмотренные выше методы оптимизации, но ниже будет рассмотрен пример синтеза шарнирного передаточного четырехзвенника методом приближения функций. Пусть и – углы, определяющие положения входного и выходного звеньев – кривошипа и коромысла, а и – углы, определяющие начала отсчета углов и соответственно. Направления отсчета положительных углов показаны на рис. 4.14.
Зависимость между углами () называется передаточной функцией.
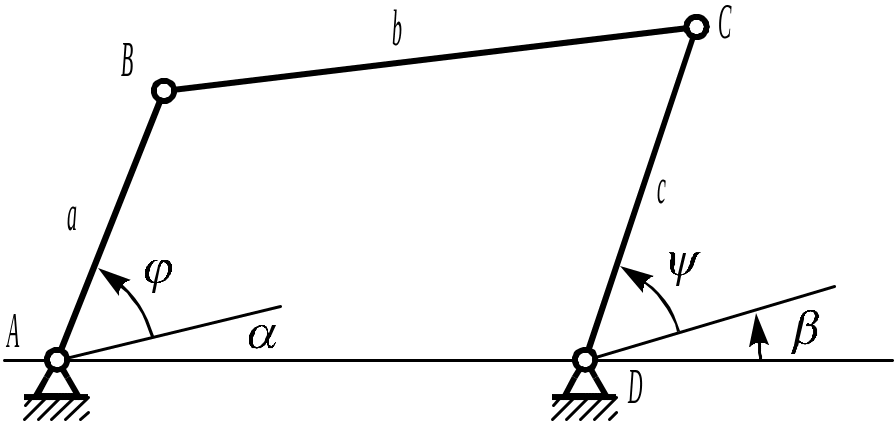
Рис. 4.88
Очевидно, что передаточный шарнирный четырехзвенник может воспроизвести точно не всякую функцию (). Для целей практики, как правило, вполне достаточно, чтобы действительно воспроизводимая передаточным механизмов функция М() мало отличалась от заданной функции ().
Рис. 4.89
Легко усмотреть зависимость функции
М от
положения механизма ,
углов и ,
а также параметров a,
b, c,
где
.
Поэтому
М=М(, , a, b, c, ).
Задача синтеза механизма передаточного шарнирного четырехзвенника сводится к определению вектора параметров R={, , a, b, c}т, при которых функция М мало отличается от функции для всех положений механизма, то есть для всех из отрезка [0,0], где 0 < 0 2 – заданная величина, определяющая конечное положение кривошипа.
Пусть мера отличия функций М и :
(R,) = М(R,) – (),
где М и – действительный и требуемый углы поворота коромысла CD.
Пусть в четырехзвенник введено пятое звено – ползун, перемещающийся по шатуну (рис. 4.15, а). В получившемся механизме, имеющем две степени свободы, кривошип и коромысло могут совершать перемещения, независимые в некоторых пределах изменения углов и . Поэтому такой механизм может осуществить движение коромысла по закону (1), но для этого расстояние между точками В и С должно изменяться. Таким образом, введение ползуна равносильно введению в четырехзвенник шатуна переменной длины bф. Очевидно, что чем меньше разность , тем меньше разность
b(R,) = b – bф(R,).
Пусть вес выбран в виде
q(R,) = b+bф(R,).
Тогда взвешенное отклонение
q(R,) = b2+bф2(R,).
При малых b, то есть при b bф, взвешенное отклонение имеет вид
q(R,) 2bb(R,).
Далее необходимо установить связь b и , для чего необходимо рассмотреть движение шарнира при закрепленном кривошипе рис. 4.15, б. Пусть коромысло повернулось на угол . При этом ось шарнира С опишет дугу окружности длиной С, точка С переместится в точку С1, а длина шатуна изменится на величину b = СхС1. При малом b треугольник СхС1 близок к прямоугольному, у которого угол между сторонами С1Сх и СС1 равен . Тогда b = с cos, а можно найти как
. (4.29)
Из рис. 4.15, б следует, что угол является углом давления, если считать, что сила давления шатуна на коромысло направлена по шатуну. Из этого же рисунка, следует:
Отсюда
.
Из (4.28) следует, что определяется по q только при =/3. Это условие, как правило, всегда выполняется так, как при синтезе механизмов всегда вводится ограничение [].
Для нахождение выражения для q из геометрических соображение находим
.
Следовательно
,
или
Это выражение содержит один аргумент и пять постоянных параметров синтеза , , a, b, c, подлежащих определению из условия малости взвешенного отклонения
q(R,) = P(R,) – F()
на заданном участке изменения угла .
В общем случае q несколько отличается от . Поэтому функции P(R,) и М, а также функции F() и () не совпадают друг с другом. Это различие, однако, несущественно, если малым соответствуют малые q.
Пусть А – постоянный коэффициент, зависящий от параметров синтеза. Тогда вместо взвешенного отклонения q можно использовать взвешенное отклонение
q = А[P(R,) – F()].
В некоторых задачах синтеза часть параметров синтеза может быть задана. За счет этого вид функций P(R,) и F() может изменяться, однако выражение для q должно оставаться неизменным.