2.2.Силовой анализ механизмов

Силовой анализ механизмов представляет собой решение первой задачи динамики системы: определение сил по заданному закону движения. Определению подлежат реакции в кинематических парах механизма. Для решения этой задачи в «Теории механизмов и машин» применяется метод кинетостатики. Метод кинетостатики это формальный прием, который позволяет записать уравнения движения в форме уравнений равновесия и, следовательно, решать задачу методами статики.

Заметим, что метод кинетостатики это не единственный способ решения этой задачи: можно, освобождаясь от связей, вводить реакции связей в уравнение движения системы и находить последние из них. Звенья механизма, находящегося в движении, в общем случае не находятся в равновесии, т.к. они движутся с ускорениями.

Однако мы можем рассматривать равновесие всего механизма и каждого звена в отдельности, если применим к решению этой задачи принцип Даламбера, который утверждает следующее: если систему, находящуюся в движении, в какой – либо момент времени мгновенно остановить и к каждой материальной точке этой системы приложить действовавшие на нее в момент остановки активные силы, реакции связей и силы инерции, то система останется в равновесии.

При определении неизвестных реакций мы будем расчленять механизм, пользуясь принципом освобождаемости от связей, т.е. будем выделять из механизма группы звеньев и отдельные звенья, рассматривать их равновесие. При этом действия отброшенных звеньев на рассматриваемые будем представлять реакциями, действующими на рассматриваемые звенья со стороны отброшенных в расчлененных кинематических парах.

2.2.1.Условие статической определимости кинематических цепей

Разделяя механизм на части и прикладывая в расчлененных кинематических парах реакции со стороны отброшенных звеньев, следует иметь в виду, что не всякая выделенная из механизма кинематическая цепь будет статически определимой системой. Статически определимой будет такая система, в которой число неизвестных (определяемых сил) будет равно числу уравнений статики. Для плоских механизмов, в состав которых входят кинематические пары 5-го и высшие пары 4-го классов и на которые действует плоская система сил, число неизвестных реакций связей совпадает с числом ограничений, имеющихся в этих кинематических парах. Так, например, соединение звеньев во вращательную кинематическую пару 5-го класса исключает возможность движения центра вращения вдоль координатных осей за счет возникновения сил, препятствующих движению в этих направлениях.

Таким образом, определению подлежат обе проекции силы реакции на координатные оси, т.е. неизвестных будет два. Если же говорить о равнодействующей силе реакции как о векторе, то неизвестными будут величина и направление силы. Третья характеристика силы – точка ее приложения – может быть условно помещена в центр шарнира (поскольку сила – это скользящий вектор). Конечно, «точка приложения» это понятие условное, так как силы реакции распределены по поверхности соприкосновения звеньев, однако равнодействующая реакции проходит через центр шарнира (рис. 2.12).

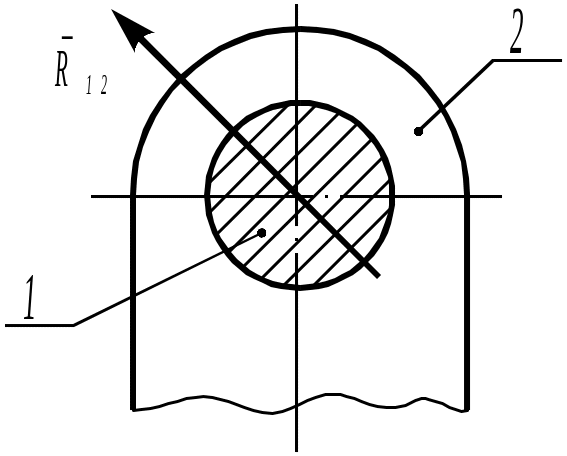
Рис. 2.39

Соединение звеньев в поступательную пару 5-го класса исключает свободу движения вдоль одной из координатных осей (этому движению препятствует сила, направленная вдаль этой оси) и свободу вращения вокруг оси, перпендикулярной координатной плоскости. Это говорит о том, что реакция создает момент, направленный против момента активных сил. Таким образом, в этой кинематической паре также имеются две неизвестные характеристики силы: величина и точка ее приложения. Обычно начало координат помещается в центр смежной вращательной кинематической пары, относительно оси которой могло бы совершаться вращение рассматриваемого звена (рис. 2.13).

Рис. 2.40

В высшей паре четвертого класса неизвестна только одна характеристика силы: ее величина, т.к. направление её (по нормали к соприкасающимся поверхностям звеньев) и точка приложения известны (рис. 2.14).

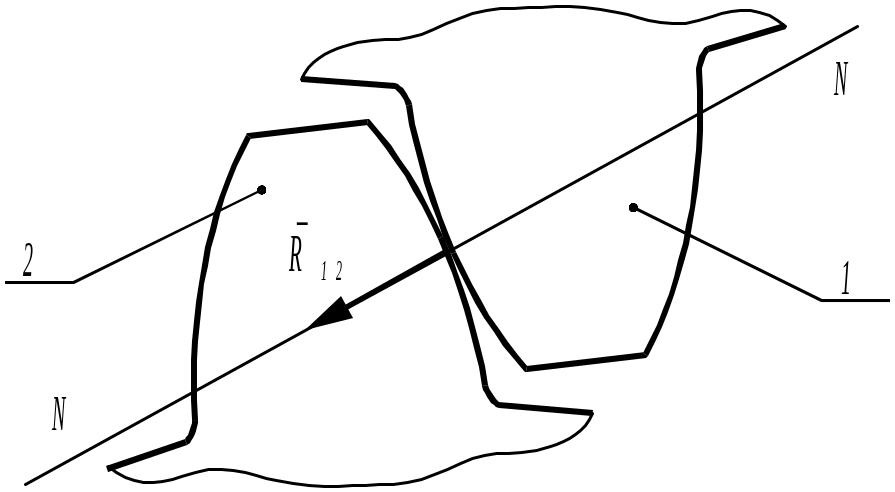
Рис. 2.41

Таким образом, если в выделенную из механизма плоскую кинематическую цепь будет входить n звеньев, то для них можно составить 3n уравнений статики (x=0, y=0, m_a=0). Число неизвестных в этих уравнениях будет соответствовать удвоенному числу кинематических пар 5-го класса плюс число кинематических пар 4-го класса, т.е. общее число неизвестных в выделенной кинематической цепи будет равно 2Р₅+Р₄. Для того чтобы кинематическая цепь была статически определимой, число уравнений должно быть равно числу неизвестных, т.е. должно удовлетворяться условие

3n = 2Р₅ + Р₄.

Этому условию удовлетворяют группы Ассура. Вот почему для определения реакций механизм расчленяется на группы Ассура.