1.6. Частные положения точки

Рассмотрим некоторые частные случаи положения точки, а именно когда точка лежит на какой-нибудь плоскости проекций или какой-нибудь оси проекций (рис. 1.7).

Если точка принадлежит какой-либо плоскости проекций, то две её проекции будут находиться на осях. Эпюр точки, лежащей на плоскости П₁, показан на рис. 1.7, а, б. Горизонтальная проекция А₁ совпадает с самой точкой. Фронтальная проекция А₂ лежит на оси Х, а профильная – на оси Y. Точки могут лежать также на фронтальной и профильной плоскости проекции.

Если точка принадлежит какой-либо оси проекций, то две её проекции будут находиться на осях, а третья проекция - в точке начала отсчета, точке О. Рассмотрим положение точки В, лежащей на оси Х. В этом случае фронтальная и горизонтальная проекции точки лежат на оси Х в одной точке, а профильная проекция – в пересечении осей (рис. 1.7, в, г).

На рис. 1.8 представлена связь эпюра Монжа с проекционным черчением и методом проецирования, принятым в курсе технического черчения в соответствии с Единой системой конструкторской документации (ЕСКД)

а)

б)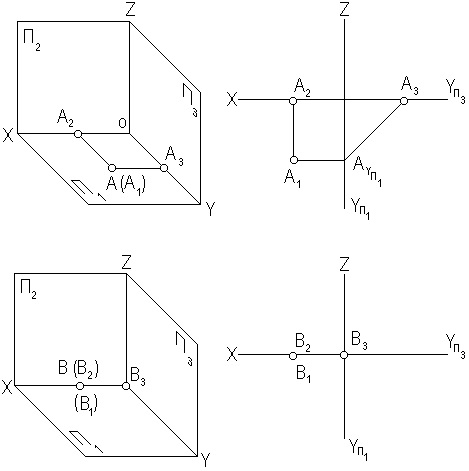

в) г)

Рис. 1.7. Проекции точек частного положения

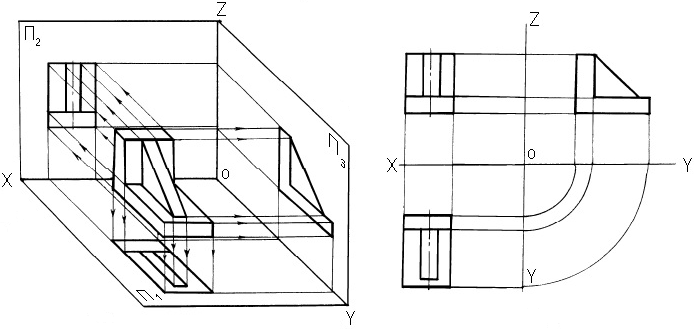
Рис. 1.8. Проекционный чертеж детали

Вопросы для самоконтроля

1. В чем суть центрального проецирования?

2. Перечислите основные свойства центрального проецирования.

3. В чем суть операции, называемой параллельным проецированием точек пространства на плоскость?

4. В чем суть ортогонального проецирования?

5. Перечислите основные свойства ортогонального проецирования.

6. Сформулируйте принципы построения чертежа, предложенные Г. Монжем.

7. Как строятся проекции точки в системе двух плоскостей проекций?

8. Как строятся проекции точки в системе трех плоскостей проекций?

9. Перечислите характеристики точек расположенных в разных октантах.

10. Какие бывают случаи частного положения точки?

ЛЕКЦИЯ №2

Проекции прямой линии

Проецирование отрезка прямой.

Расположение отрезка относительно плоскостей проекций.

Взаимное положение точки и прямой в пространстве.

Взаимное положение прямых в пространстве.

2.1. Проецирование прямой линии

Отрезок прямой линии определяется двумя точками. Следовательно, проекции двух точек определяют проекции отрезка прямой (рис. 2.1). Проекции отрезка прямой в общем случае всегда будут меньше самого отрезка прямой. В общем случае по проекциям отрезка прямой нельзя определить углы наклона отрезка прямой к плоскостям проекций.

2.2. Прямые общего и частного положения

Прямые подразделяются на прямые общего и частного положения. Прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется прямой общего положения (рис. 2.1, а).

Прямые, параллельные или перпендикулярные плоскостям проекций, называются прямыми частного положения (рис. 2.1, б, в). Прямые, параллельные плоскостям проекций, называются по имени плоскости, которой они параллельны: горизонталь h, фронталь f и профильная прямая w.

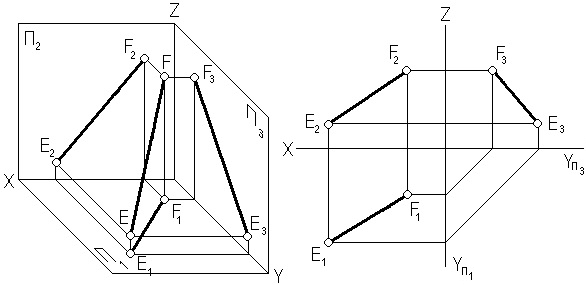
а) EF – прямая общего положения

h (АВ)║П₁ f (СD)║П₂ w (ЕК)║П₃

б) прямые, параллельные плоскостям проекций

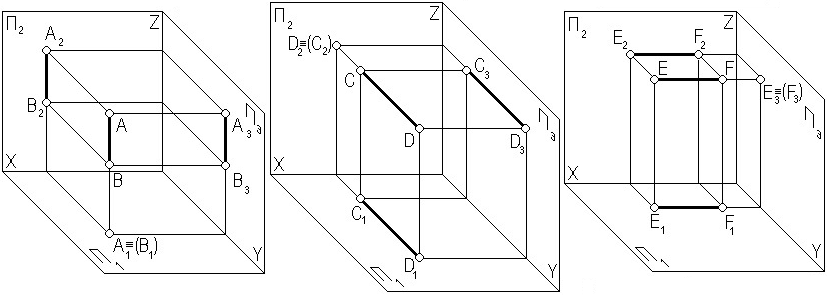
АВП₁ СDП₂ ЕFП₃

в) прямые, перпендикулярные плоскостям проекций (проецирующие прямые)

Рис. 2.1. Прямые общего и частного положений

Прямые, перпендикулярные плоскостям проекций, называются проецирующими: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая, в зависимости от плоскости, к которой они перпендикулярны.

Прямая может лежать на плоскости проекций. На рис. 2.2, а изображена прямая, лежащая на горизонтальной плоскости проекций П₁. Прямая может лежать также на плоскостях П₂ и П₃.

Прямая может лежать на осях проекций. На рис. 2.2, б изображена прямая, лежащая на положительном направлении оси Y. Прямая может лежать и на осях Х и Z.

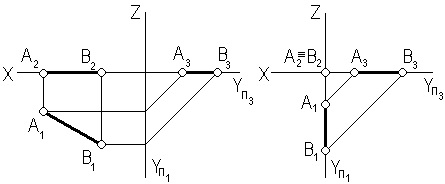
а) б)

Рис. 2.2. Эпюры прямых