9.3. Развертки кривых поверхностей

Развертки развертываемых кривых поверхностей можно построить методом нормального сечения и методом раскатки.

Разверткой прямого кругового конуса является сектор окружности с радиусом, равным длине образующей конуса и углом при вершине конуса.

Разверткой прямого кругового цилиндра является прямоугольник шириной, равной высоте цилиндра и длиной, равной длине окружности основания.

Сечение прямого кругового конуса, основание которого расположено в горизонтальной плоскости П₁, фронтально-проецирующей плоскостью Р рассмотрено на рис. 9.5. В зависимости от расположения секций плоскости Р относительно оси прямого кругового конуса получаются различные фигуры сечения, ограниченные кривыми линиями. Фигура сечения в данном случае будет ограничена эллипсом.

Фронтальная проекция фигуры сечения расположена на фронтальном следе плоскости Р_П2 (рис. 9.5, а). Горизонтальную проекцию контура фигуры сечения - окружность делят, например, на 12 равных частей. Через точки деления на горизонтальной и фронтальной проекциях проводят вспомогательные образующие. Находят фронтальные проекции точек 1₂, …, 12₂, лежащих на плоскости P_П2. Затем с помощью линии связи находят их профильные проекции. Найденные проекции точек контура сечения соединяют по лекалу.

Натуральная величина фигуры сечения в данном примере найдена способом замены плоскости проекций. Горизонтальная плоскость проекций П₁ заменяется новой плоскостью проекции П₄.

На фронтальной плоскости проекции П₂ фигура сечения - эллипс изображается в виде отрезка 1₂7₂, совпадающего с фронтальной проекцией секущей плоскости Р. Отрезок 1₂7₂ является большой осью эллипса. Малая ось эллипса перпендикулярна большой оси 1₂7₂. Чтобы найти малую ось сечения, через середину большой оси 1₂7₂ эллипса проводят горизонтальную плоскость N (на рисунке видим фронтальный след плоскости N_П2) которая рассечет конус по окружности, диаметр которой будет равняться малой оси эллипса АВ.

Построение развертки поверхности конуса (рис. 9.5, б) начинают с проведения дуги окружности радиусом, равным длине образующей конуса, из точки S. Длина дуги определяется углом α:

α = 180⁰ *(d/l),

где d - диаметр окружности основания конуса;

l - длина образующей конуса.

Дугу делят на 12 частей, и полученные точки соединяют с вершиной S. От вершины откладывают натуральные длины образующих от вершины конуса до секущей плоскости Р.

Натуральные размеры этих отрезков находят, как и в примере с пирамидой, способом вращении около вертикальной оси, проходящей через вершину конуса. Так, например, чтобы получить действительную длину отрезка S2 (рис. 9.5, а), надо из 2₂ провести горизонтальную прямую до пересечения с контурной образующей конуса, являющейся действительной ее длиной.

К развертке конической поверхности пристраивают фигуры сечения и основания конуса.

9.4. Развертки неразвертываемых поверхностей

По возможности развертываться кривые поверхности делятся на развертываемые и неразвертываемые (условно-развертываемые). Развертки условно развертываемых поверхностей могут быть выполнены только приближенно путем аппроксимации отсеков поверхностей.

Аппроксимация – это приближенная замена отсеков неразвертываемой поверхности отсеками развертываемой поверхности. В качестве аппроксимирующих поверхностей используют плоскости, конические и цилиндрические поверхности.

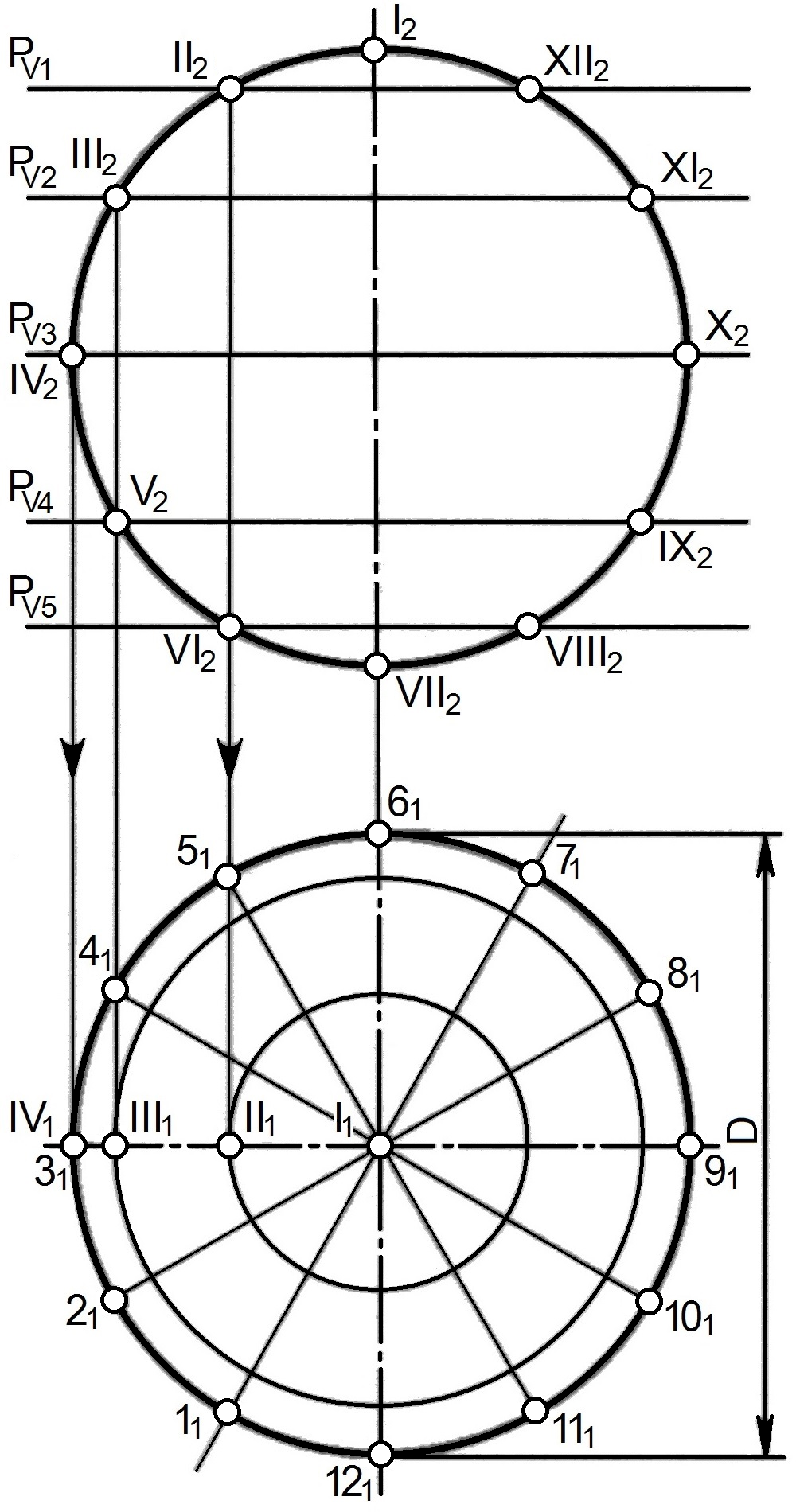
К неразвертываемым поверхностям относится поверхность сферы. Для построения развертки сферы её горизонтальную проекцию делим горизонтально-проецирующими плоскостями на несколько равных частей (клиньев), например на 12 (рис. 9.6, а). Фронтальную проекцию сферической поверхности тоже делят на несколько равных частей (желательно на 12).

Через полученные точки деления II, ..., VI проводят фронтально-проецирующие плоскости Р_V1, ..., P_V5 (рис. 9.6, а).

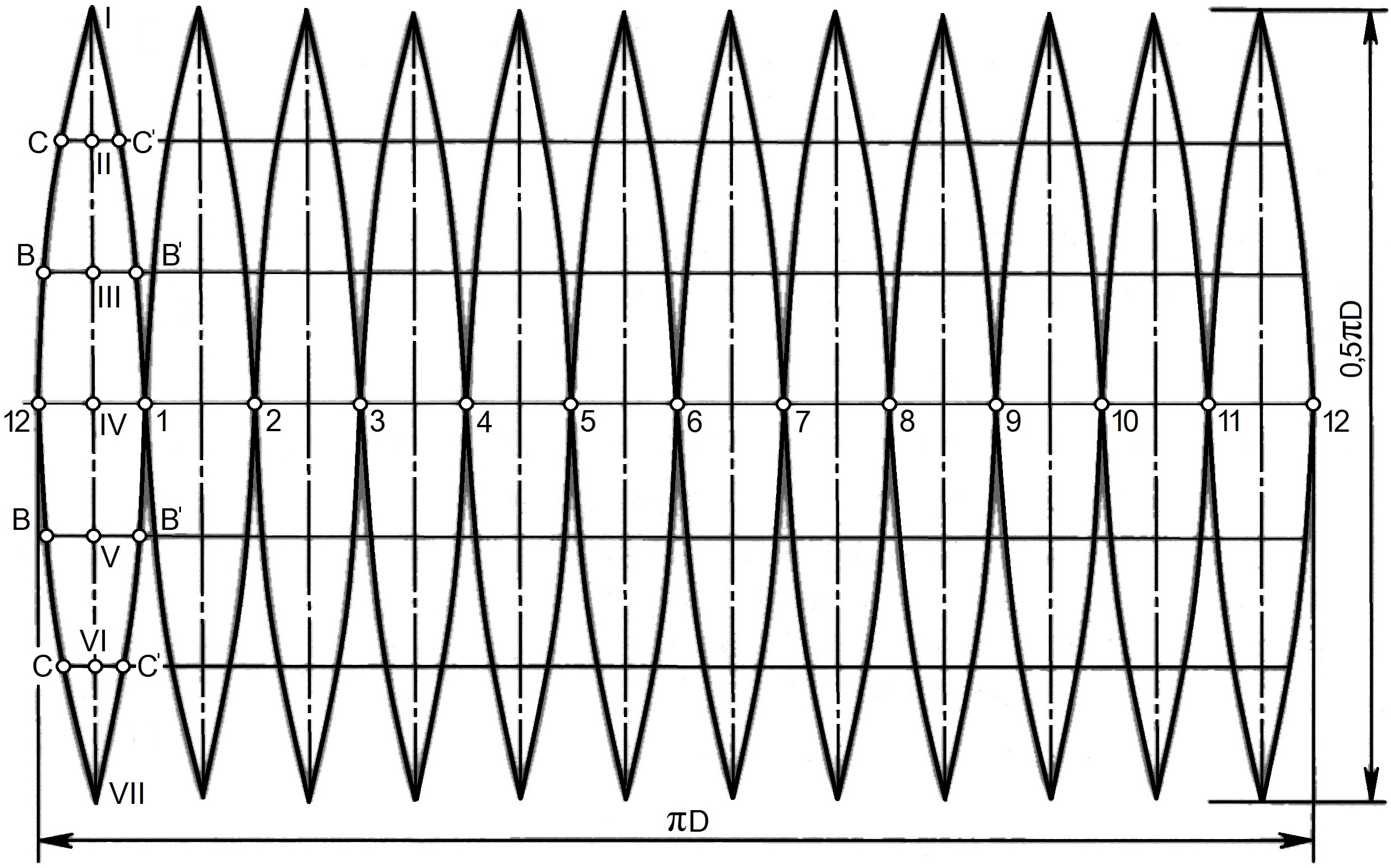
Для построения развертки сферической поверхности на горизонтальной прямой откладывают длину окружности диаметра D, равную πD (рис. 9.6, б). Полученный отрезок делят на 12 равных частей.

а)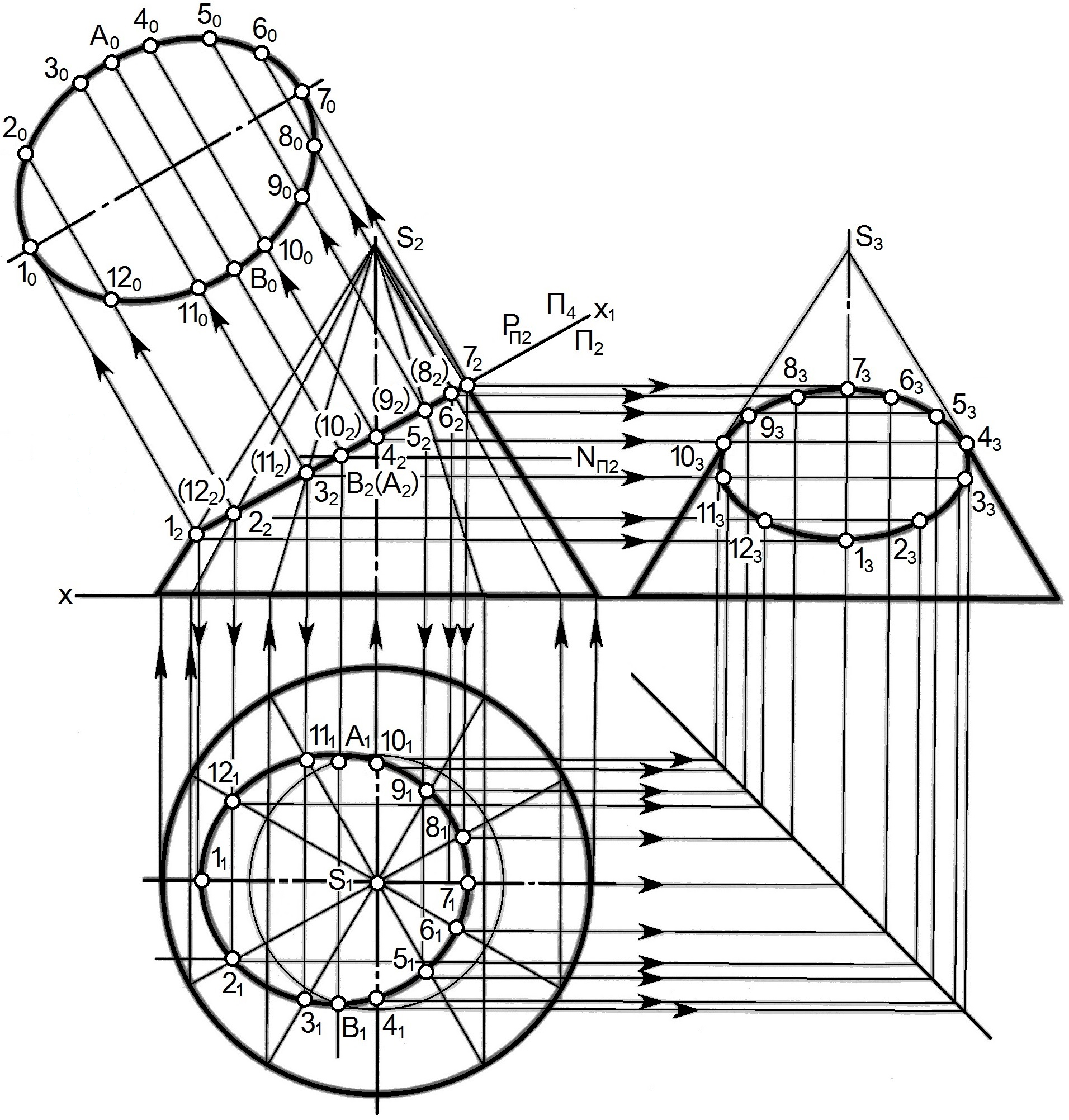

б)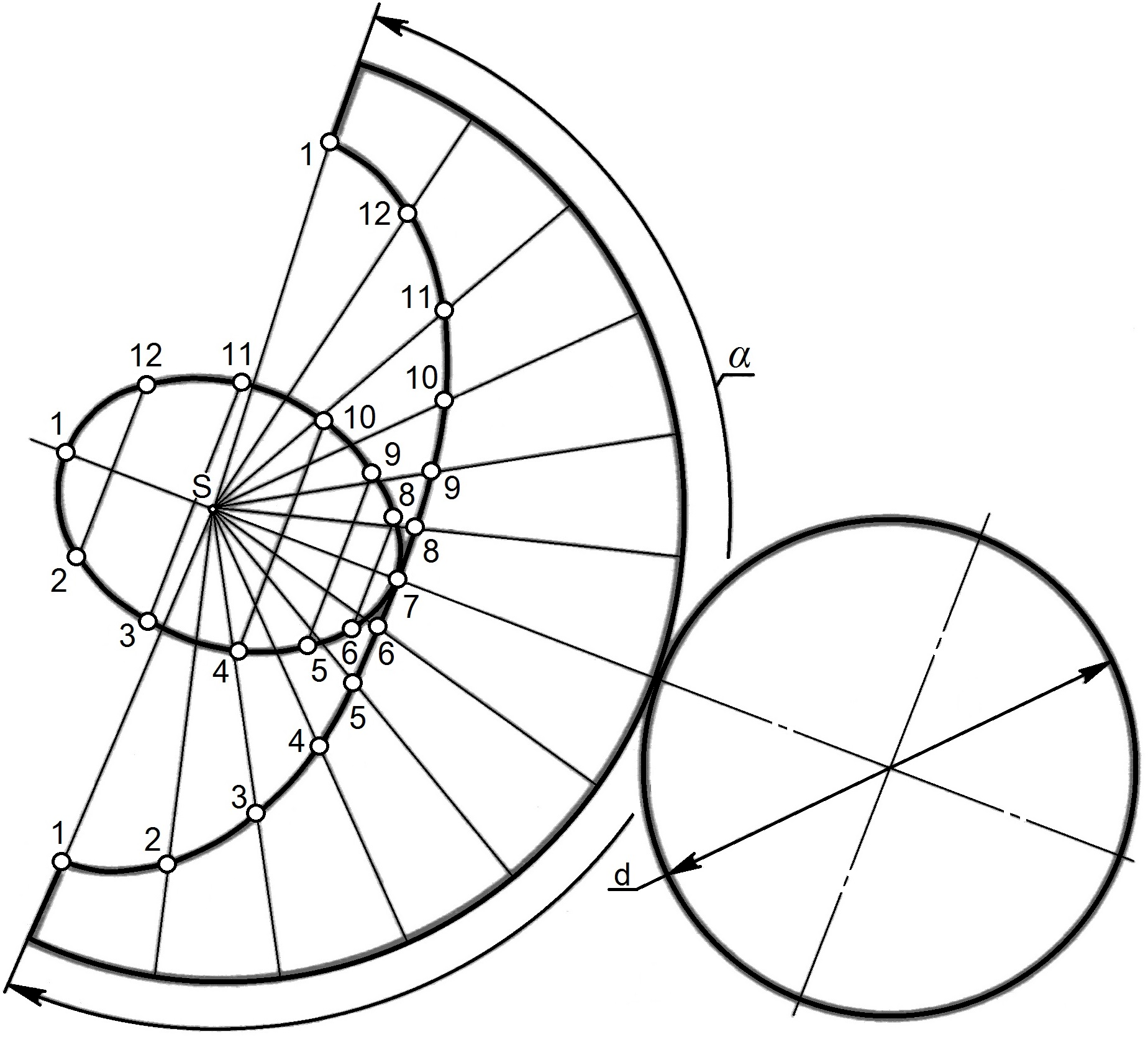

Рис. 9.5. Выполнение развертки боковой поверхности конуса

а)

б)

Рис. 9.6. Выполнение развертки боковой поверхности сферы

Через середину каждого деления проводят перпендикуляр и откладывают на нем отрезок I -VII, равный 0,5 длине окружности диаметра D. Отрезок делят на 6 равных частей, через полученные точки деления проводят горизонтальные прямые, на которых откладывают отрезки, равные 1/12 части окружности соответствующего радиуса, например, отрезок CC' соответствует 1/12 длины окружности радиуса I-II, взятого с горизонтальной проекции. Полученные точки соединяют по лекалу. Развертки остальных одиннадцати клиньев строят аналогично.

Вопросы для самоконтроля

1. Что называется разверткой поверхности?

2. Для чего нужны развертки?

3. Какими линиями на чертеже изображаются линии сгиба разверток?

4. Каким методом можно найти натуральной величины бокового ребра пирамиды для построения её развертки?

5. В чем суть метода нормального сечения?

6. В чем суть метода раскатки?

7. Порядок построения развертки многогранника.

8. Порядок построения развертки кривой поверхности.

9. Что такое аппроксимация?

10. В чем особенности выполнения разверток неразворачиваемых поверхностей?