1.2. Параллельное проецирование

Параллельное проецирование осуществляется не из центра проекций, а параллельно направлению проецирования S (рис. 1.2). В этом случае проекции точек называют параллельными проекциями. Параллельное проецирование подразделяется на косоугольное (угол между проецирующей прямой и плоскостью проекций не равен 90⁰) и прямоугольное или ортогональное (угол равен 90⁰). Свойства параллельного проецирования аналогичны свойствам центрального проецирования.

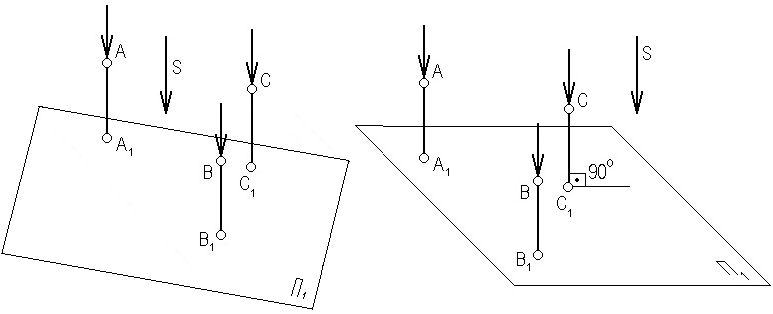
а) б)

Рис. 1.2. Параллельное проецирование

1.3. Ортогональное проецирование на одну плоскость проекций

Ортогональное проецирование является частным случаем параллельного проецирования. Оно заключается в проведении проецирующей прямой через объект перпендикулярно плоскости проекций П₁ (рис. 1.2, б).

Кроме вышеуказанных свойств центрального проецирования можно привести дополнительно следующие свойства ортогонального проецирования:

1. Прямая и плоскость, параллельные плоскости проекций, проецируются на неё в натуральную величину (НВ).

2. Проекции прямой и плоскости, не параллельных плоскости проекций, всегда меньше самих прямой и плоскости.

3. Проекции прямой и плоскости, перпендикулярных плоскости проекций, отображаются соответственно в точку и прямую.

1.4. Ортогональное проецирование на две плоскости проекций

В связи с тем, что одна проекция точки однозначно не определяет положение точки в пространстве, применяется проецирование на две плоскости проекций (рис. 1.3, а).

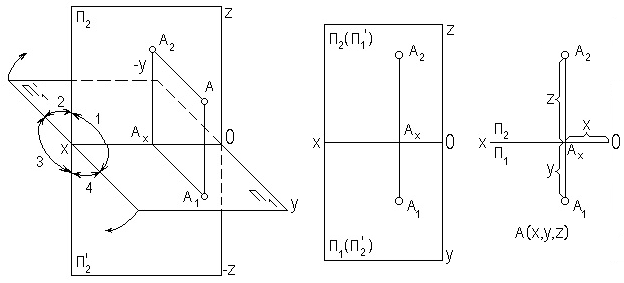
а) б) в)

Рис. 1.3. Проецирование точки на две плоскости

При проецировании на две плоскости проекций в аппарат проецирования вводятся дополнительно линии связи A₁A_х и A_хA₂. Плоскости проекций располагаются под углом 90⁰ друг к другу. Плоскость проекций П₁ назовем горизонтальной плоскостью проекций, а плоскость П₂ – фронтальной плоскостью проекций. В системе двух плоскостей проекций П₁ и П₂ выделяют оси проекций: ОX – ось абсцисс, ОY – ось ординат, ОZ – ось аппликат. Направление оси ОX влево, оси ОY к наблюдателю, оси ОZ вверх приняты за положительные. Обратные направления приняты за отрицательные.

Проекция точки на горизонтальную плоскость проекций называется горизонтальной проекцией, а проекция на фронтальную плоскость – фронтальной проекцией. Две проекции точки однозначно определяют положение точки в пространстве. Преобразуем пространственный макет, представленный на рис.1.3, а, в плоскостной. Для этого удалим саму точку, оставим лишь её проекции и линии связи. Плоскость проекций П₁ повернем вокруг оси ОX так, как показано на рис. 1.3, а, до совмещения с плоскостью П₂ (рис. 1.3, б). Далее удалим плоскости проекций и будем их только подразумевать. В результате преобразований получится плоскостной чертеж (рис. 1.3, в), который называют комплексным чертежом точки или эпюром Монжа. На эпюре указаны координаты точки, по которым можно определить положение точки в пространстве.