7.8. Пересечение поверхности прямой линией

Решение задачи о пересечении прямой с поверхностью геометрического тела осуществляется по методике, аналогичной методике решения задачи о пересечении прямой с плоскостью. Через прямую проводят вспомогательную плоскость частного положения, строят сечение геометрического тела вспомогательной плоскостью и находят общие точки прямой и построенного сечения. Полученные точки являются точками встречи прямой с поверхностью геометрического тела (точки входа и выхода). Таким образом, задача сводится к решению задачи о построении сечения геометрического тела плоскостью частного положения.

Если заданная прямая не пересекает полученный контур сечения, это означает, что прямая с поверхностью фигуры не пересекается.

На рис. 7.10 для определения точек пересечения прямой с поверхностью пирамиды используется фронтально-проецирующая плоскость α. Все остальные построения понятны из чертежа.

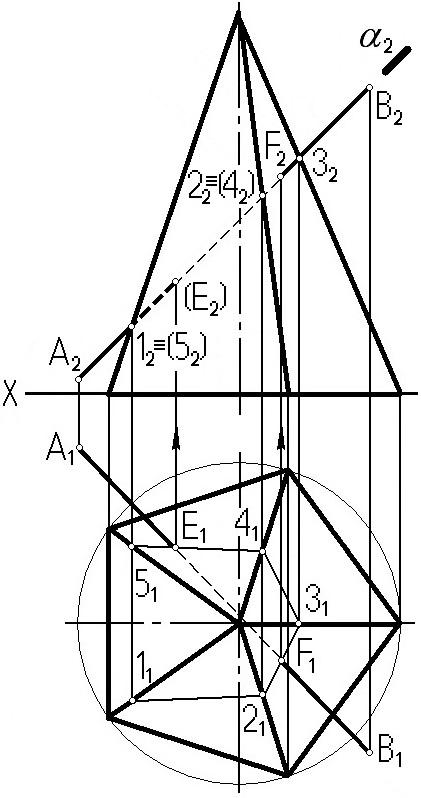
Рис. 7.10. Пересечение пирамиды прямой линией

Если прямая занимает частное положение, то задача значительно упрощается (рис. 7.11, а), т.к. заключив прямую во вспомогательную плоскость, сразу получают в сечении простую геометрическую фигуру, в данном случае - окружность радиуса R.

В случае пересечения прямой общего положения с конусом в качестве вспомогательной плоскости используют плоскость общего положения, проходящую через вершину конуса S. Вспомогательную плоскость задают двумя пересекающимися прямыми EF и S3 (рис. 7.11, б). В сечении конуса такой вспомогательной плоскостью образуется треугольник. Определим следы прямых, для прямой EF – это будет точка М', а для прямой S3 – точка М. Через найденные проекции следов М₁ и М'₁ проведём горизонтальный след вспомогательной плоскости α₁. Отметив точки 1 и 2, соединим их с вершиной конуса S. Таким образом, контур сечения представляет собой треугольник 1,2,S.

Там, где контур сечения пересекает заданная прямая EF, там и будут точки пересечения К и N прямой с поверхностью конуса.

При решении данной задачи использование в качестве вспомогательных горизонтально- или фронтально-проецирующих плоскостей нерационально, так как они в сечениях образуют эллипс и гиперболу, построение которых связано с большой трудоемкостью и неточностью.

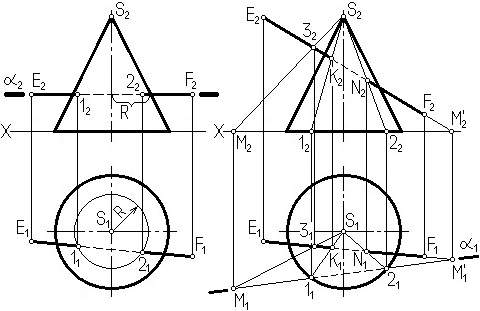
а) б)

Рис. 7.11. Пересечение конуса прямой линией

В некоторых случаях для упрощения решения применяют методы преобразования для того чтобы получить в сечении более удобные для построения кривые линии, например, окружность известного диаметра (рис. 7.12).

Для определения точек пересечения через прямую АВ проведена вспомогательная плоскость Σ, перпендикулярная плоскости П₂, т.е. фронтально-проецирующая плоскость. Эта плоскость пересечёт сферу по окружности диаметром d. Затем заменяем плоскость П₁ на плоскость П₄. Плоскость П₄ параллельна вспомогательной плоскости Σ, в которой лежит прямая АВ и окружность, по которой вспомогательная плоскость пересекает сферу. Окружность проецируется на плоскость П₄ без искажения. Точки пересечения N₄ и M₄ прямой АВ c окружностью и являются искомыми (рис. 7.12).

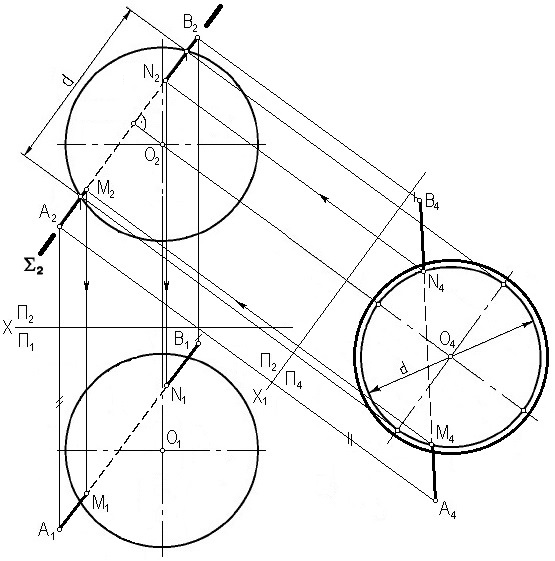
Рис. 7.12. Пересечение сферы прямой линией