Прояв показників сукупності центральної тенденції

Якщо розподіл для контрольної групи і для фонових значень в дослідній групі більш або менш симетричні, то значення, отримані в експериментальній після впливу, групуються, як вже говорилось, більше в лівій частині кривої. Це говорить про те, що після вживання сильного тютюну виявляється тенденція до погіршення показників у більшого числа досліджених.

Для того щоб виразити подібні тенденції якісно, використовують три типи показників моду, медіану та середню.

1. Мода (М₀) - це самий простий з всіх трьох показників. Вона відповідає або найбільш частому значенню, або середньому значенню класу з найбільшою частотою. Так, в нашому прикладі для експериментальної групи мода для фону буде дорівнювати 15 (цей результат зустрічається чотири рази та знаходиться в середині класу 14-15-16), а після впливу – 9 (середина класу 8-9-10)

Мода використовується рідко і головним чином для того, щоб дати загальне представлення про розподіл. В деяких випадках у розподілі можуть бути дві медіани; тоді говорять про бімодальний розподіл. Така картина вказує на те, що в даній сукупності маються дві відносно самостійні групи.

2. Медіана (М_е) відповідає центральному значенню в послідовному ряду всіх отриманих значень.

У випадку якщо число даних , парне, медіана дорівнює середній арифметичній між значеннями, які знаходяться в ряду на му і -му місцях. Так, для результатів впливу для восьми юнаків дослідної групи медіана розташовується між значеннями, які знаходяться на 4-м (8/2=4) і на 5-му місцях в ряду. Якщо вписати весь ряд для цих даних, а саме

7 8 11 12 13 14 16,

то виявиться, що медіана відповідає (11+12)/2=11,5

3. Середнє арифметичне ( ) (далі просто «середня»)- це найбільш часто використаний показник центральної тенденції. Її застосовують, зокрема, в розрахунках , необхідних для опису розподілу і для його подальшого аналізу. Її обчислюють, розділивши суму всіх значень даних на число цих даних. Так, для нашої експериментальної групи вона складає 15,5 (228/15) для фона і 11,3 (169/15) для результатів впливу.

Якщо тепер відмітити всі ці три параметри на кожній з кривих для експериментальної групи, то буде видно, що при нормальному розподілі вони більш або менш співпадають, що показано нижче.

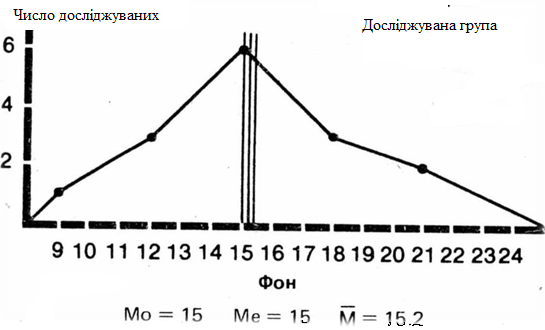
Рис. 4.9

Оцінка розподілу

Найчастіше всього для оцінки розподілу визначають відхилення кожного з отриманих значень від середньої ( ), позначуване літерою , а потім обчисляють середнє арифметичне всіх цих відхилень. Чим вона більше, тим більше розподіл даних и тим більш різнорідна вибірка. Навпроти, якщо ця середня невелика, то дані більш сконцентровані відносно їх середнього значення і вибірка більш однорідна.

Таким чином,перший показник, використовується для оцінки розподілу, - це середнє відхилення. Його обраховують наступним чином (приклад, який ми тут наведемо, не має нічого спільного з експериментом № 1. Зібравши всі дані та розташувавши їх в ряд 3 5 6 9 11 14, психолог знаходить середню арифметичну для вибірки:

Потім обраховують відхилення кожного значення від середньої та додають їх:

Однак при такому складанні негативні та позитивні відхилення будуть знищувати одне одного, іноді навіть повністю, так що результат може бути рівним 0. З цього ясно, що треба знаходити суму абсолютних значень індивідуальних відхилень і вже цю суму ділити на загальне число. При цьому отримуємо наступний результат:середнє відхилення дорівнює

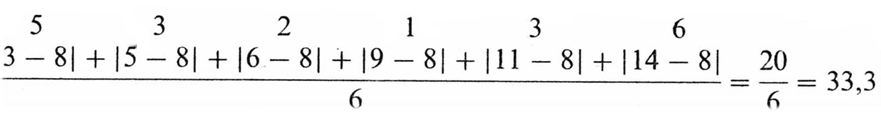
Загальна формула:

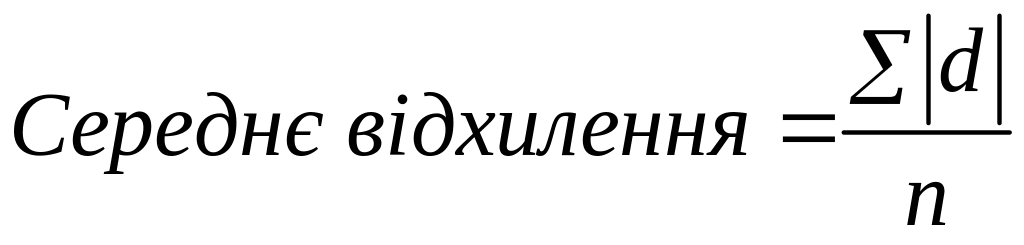
де (сігма) означає суму; - абсолютне значення кожного індивідуального відхилення від середнього значення; n - число даних.

Однак абсолютними значеннями доволі важко оперувати в алгебраїчних формулах , які використовуються в більш складному статистичному аналізі. Щоб відмовитись від значень з негативним знаком потрібне зведення всіх значень в квадрат, а потім ділити суму квадратів на число даних. В нашому прикладі це виглядає наступним чином:

В результаті такого обчислення отримують так звану варіансу. Формула для обрахування варіанси, таким чином, наступна:

Нарешті, щоб отримати показник, що можна порівняти за величиною з середнім відхиленням, статистики вирішили знаходити з варіанси квадратний корінь. При цьому отримуємо так зване стандартне відхилення:

В нашому прикладі стандартне відхилення дорівнює

_{Слід ще додати, що для того, щоб більш точно оцінити стандартне відхилення для малих вибірок (з числом елементів менше 30), в знаменнику вираз під коренем треба використовувати не n, а n-1:}

_{Повернемось тепер до нашого експерименту № 1та подивимось, наскільки корисним виявиться цей показник для опису вибірок.}

_{На першому етапі, зрозуміло, необхідно обрахувати стандартне відхилення для всіх чотирьох розподілів. Зробимо це спочатку для фону дослідної групи.}

Таблиця 4.8

_{Розрахунок стандартного відхилення для фону контрольної групи в експерименті № 1}

Досліджувані	Число поцілених мішеней в серії	Середнє	відхилення від середнього	Квадрат відхилення від середнього
1 2 3 . . 15	19 10 12 . . 22	15,8 15,8 15,8 . . 15,8	-3,2 +5,8 +5,8 . . -6,2	10,24 33,64 14,44 . . 38,44

_{Про що ж свідчить стандартне відхилення, рівне 3,07?. Виявляється, воно дозволяє сказати, що більша частина результатів (виражених тут числом поцілених мішеней) розташовується в межах 3,07 від середнього значення, тобто між 12,73 (15,8-3,07) та 18,87 (15,8+3,07).}

_{Для того щоб краще зрозуміти, що є під «великою частиною результатів», треба спочатку розглянути ті властивості стандартного відхилення, які проявляються при вивченні популяції з нормальним розподілом.}

_{При нормальному розподілі «більша частина» результатів, яка розташовується в межах одного стандартного відхилення по обидві сторони від середньої, у відсотковому співвідношенні завжди одна і та ж не залежить від величини стандартного відхилення: вона відповідає 68% популяції (тобто 34% її елементів розташовуються зліва і 34 %  справа від середнього значення):}

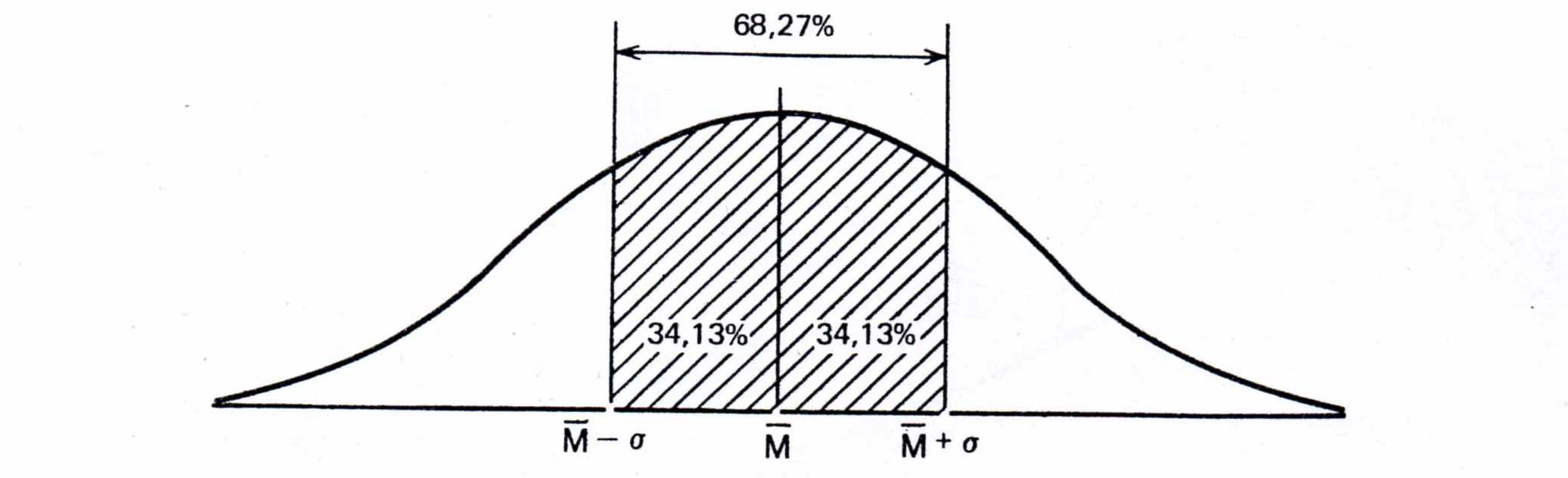
Рис. 4.10

Так само розрахували, що 94,45% елементів популяції при нормальному розподілі не виходить за межі двох стандартних відхилень від середнього значення:

Рис. 4.11

І що в межах трьох стандартних відхилень вміщується все популяція  99, 73%.

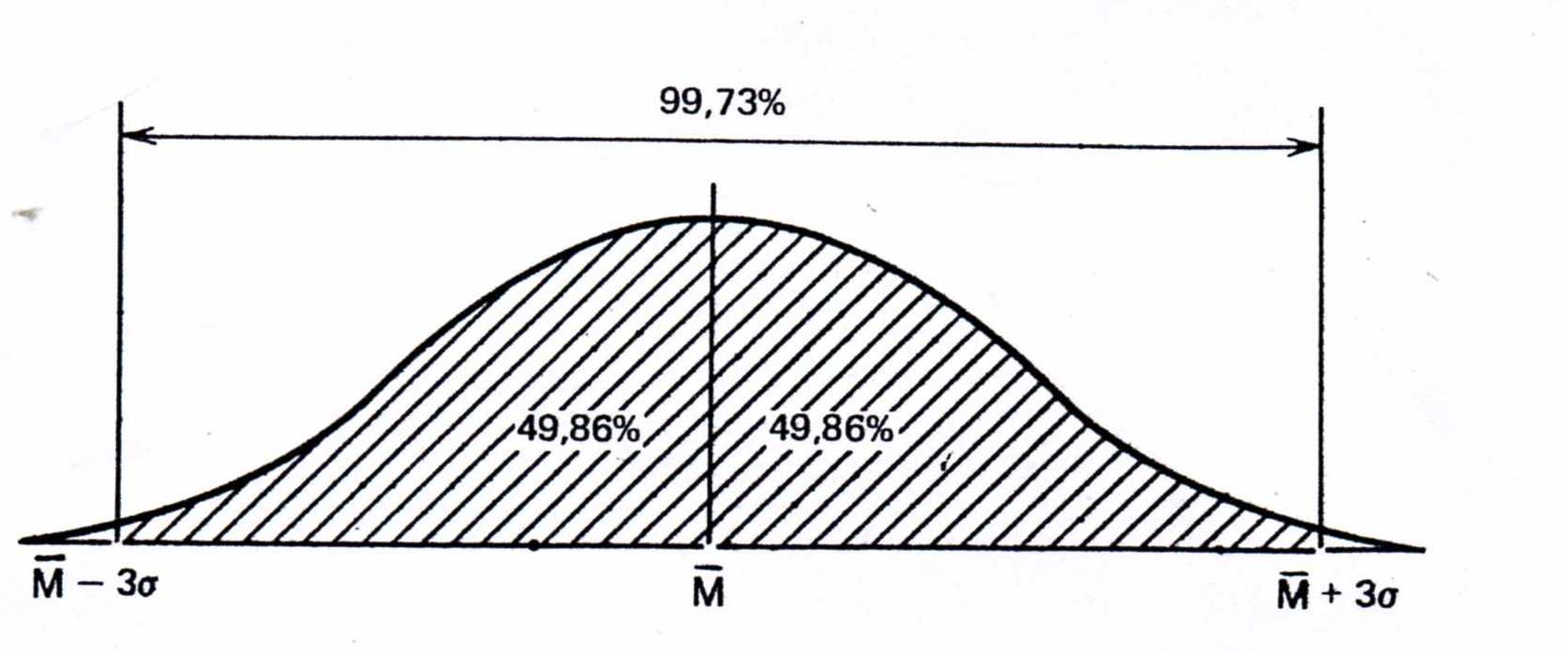
Рис. 4.12

Враховуючи, що розподіл частот фону контрольної групи доволі близький до нормального, можна припустити, що 68% членів усієї популяції, з якої взята вибірка, теж буде отримувати подібні результати, тобто потрапляти приблизно в 13-19 мішеней з 25. Розподіл результатів інших членів популяції повинні виглядати наступним чином:

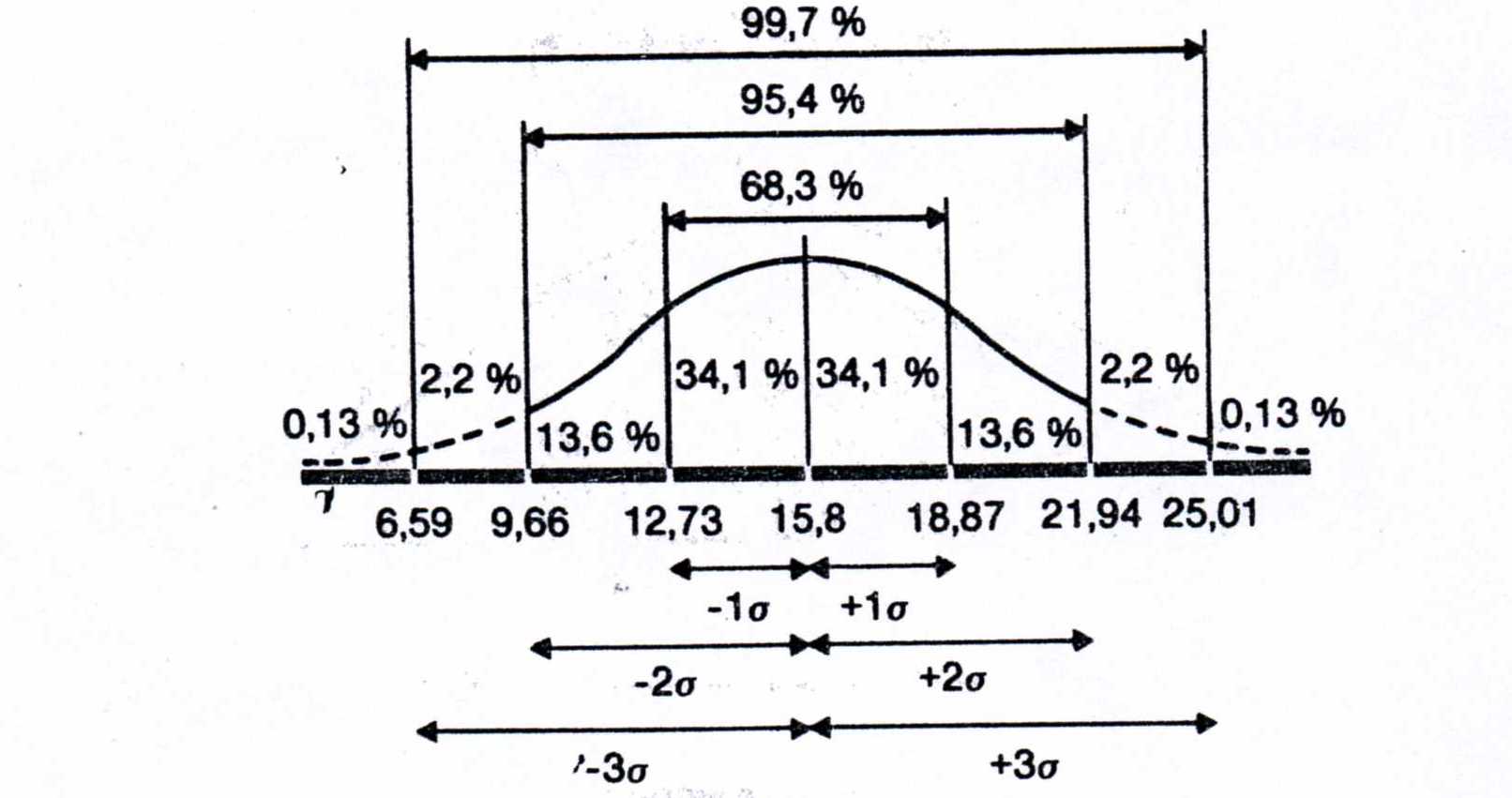
Рис. 4.13

Гіпотетична популяція, з якої взята контрольна група (фон).

Що ж стосується результатів тієї ж групи після дії досліджуваного фактору, то стандартне відхилення для них виявилось рівним 4,25 (поцілених мішеней). Таким чином можна припустити, що 68% результатів будуть розташовуватись саме в цьому діапазоні відхилення від середньої, яка складається з 16 мішеней, тобто в межах від 11,75 (16-4,25) до 20,25 (16+4,25), чи, округлюючи, 12-10 мішеней з 25. Помітно, що розподіл результатів тут більший, ніж у фоні. Цю різницю в розподілі між двома вибірками для контрольної групи можна графічно представити наступним чином:

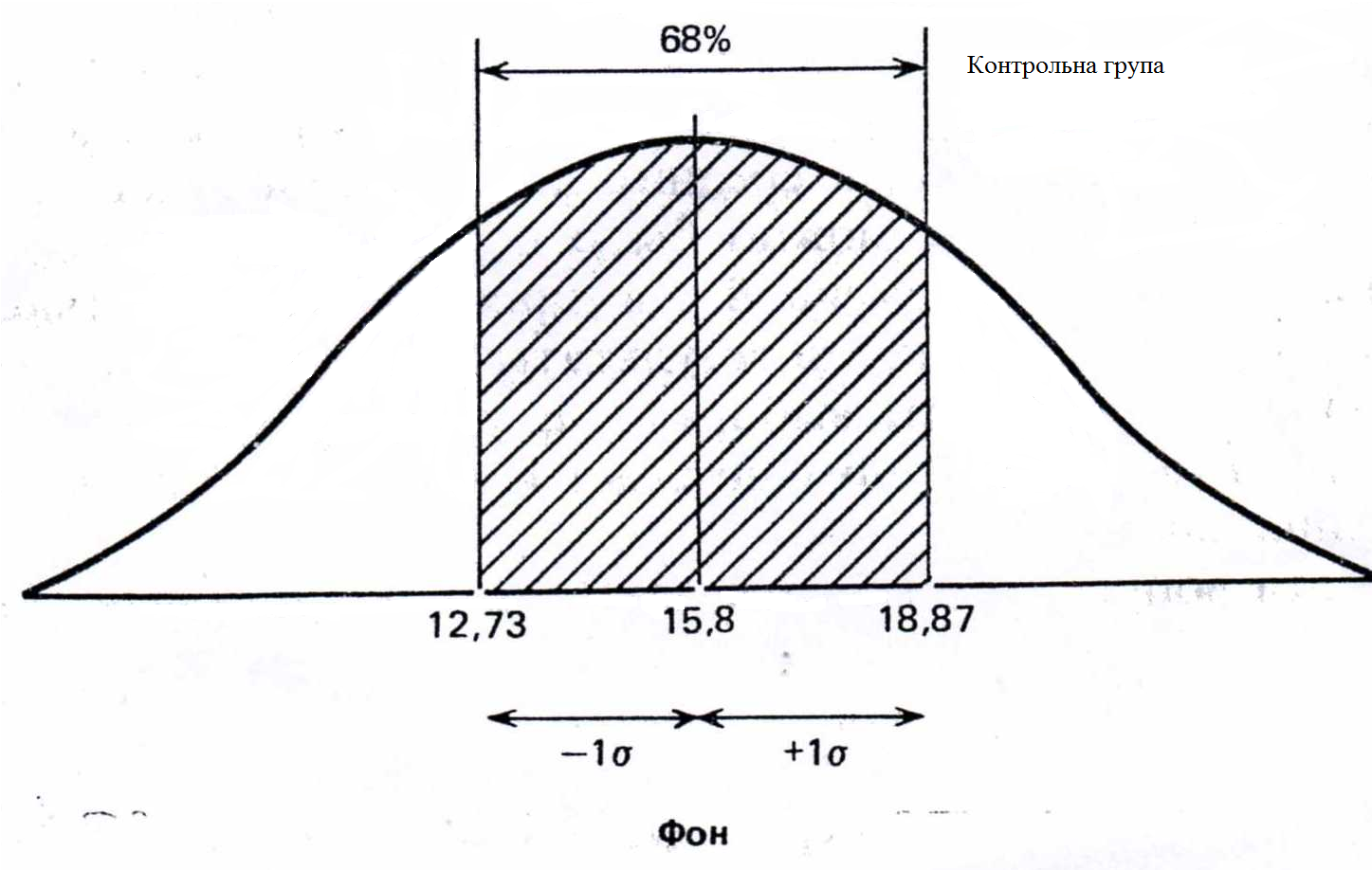
Рис. 4.14