Unlock-Линейная алгебра Сикорская 1
.pdf
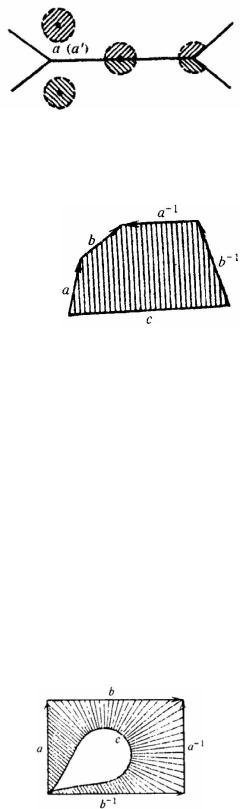
Рисунок 124
Аналогичным образом можно склеивать две стороны одного многоугольника (см. примеры п. 1).
Рисунок 125
Перейдем к склеиваниям поверхностей. Склеим в пятиугольнике, изображенном на рисунке 125, стороны, обозначенные одинаковыми буквами. Стрелки указывают закон склеивания соответствующих сторон (начало ориентированного отрезка склеивается с началом другого, конец – с концом). Показатель −1 при буквенном обозначении некоторых сторон напоминает о несовпадении для этих сторон направления, задаваемого стрелками, с направлением, задаваемым обходом многоугольника по часовой стрелке. Удобное описание схемы склейки можно получить, записывая последовательно обозначения сторон в «слово», обходя многоугольник по часовой стрелке.
Например, если начинать со стороны a , то схема склейки будет aba−1b−1c . Такая схема характеризует склейку, так как полностью определяет в многоугольнике склеиваемые стороны и закон склеивания. Нетрудно убедиться, что это факторпространство можно получить и другим топологически эквивалентным способом (рисунок 126).
Рисунок 126
Здесь факторпространство представляет тор с вырезом по кривой c (рисунок 127, где штриховыми линиями обозначены линии склейки aa−1 и bb−1 ).
360
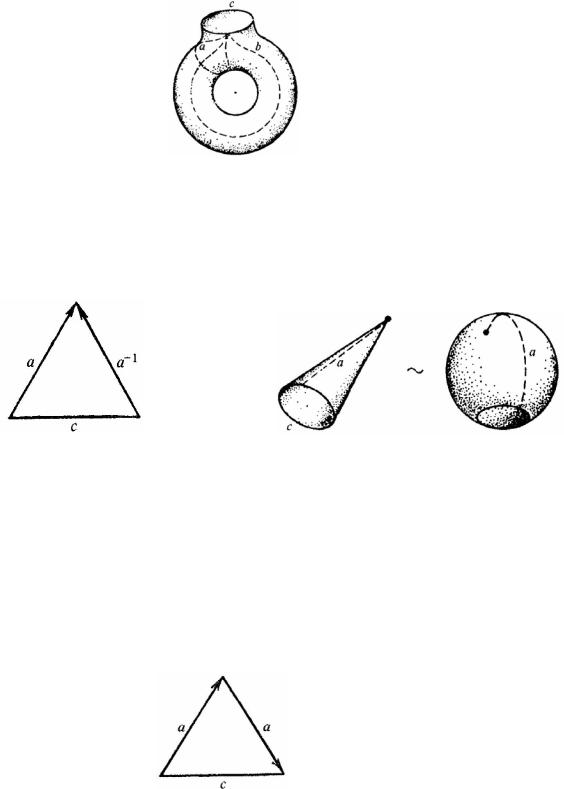
Рисунок 127
Top с дырой называется ручкой.
Рассмотрим склейку соседних сторон треугольника. Если ориентации
противоположны, т. е. схема склейки aa−1c (рисунок 128), то факторпространство топологически эквивалентно сфере с дырой (рисунок 129).
Рисунок 128 |
Рисунок 129 |
Рассмотрим склейку соседних сторон с одинаковой ориентацией, т. е. по схеме aac (рисунок 129). Этот треугольник представим как результат склейки двух прямоугольных треугольников по общей высоте d (рисунок 131) с указанной ориентацией. Поменяем порядок склейки этих треугольников: сначала отождествим гипотенузы a , а затем катеты d (рисунок 132). Получится лист Мёбиуса, причем последнее факторпространство гомеоморфно исходному (рисунок 130).
Рисунок 130
361
|
|
|
|
Рисунок 131 |
Рисунок 132 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 133 |
Рисунок 134 |
Теперь, вырезав в сфере S 2 кружок, можно к сфере с дырой приклеить либо ручку, либо лист Мёбиуса по свободному краю c ; последний можно
представлять как окружность S1 (граница вырезанного кружка). В первом случае получаем тор (рисунок 133) (убедитесь в топологической эквивалентности фигур
на рисунке). Во втором – проективную плоскость RP2 . Убедимся в этом. Проективная плоскость топологически эквивалентна факторпространству,
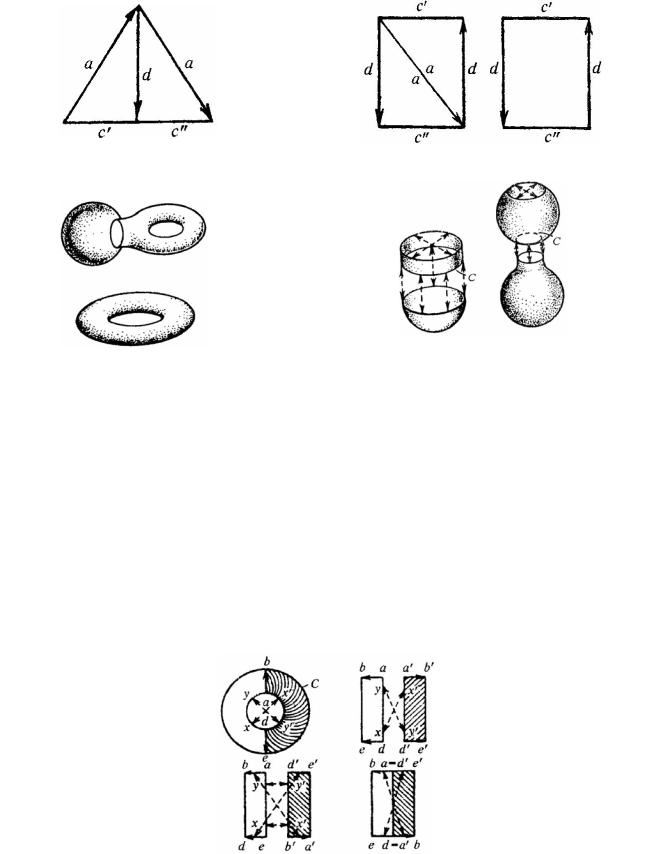
изображенному на рисунке 134. Действительно, остается показать, что верхний «колпачок» (рисунок 134) – лист Мёбиуса с краем c . Представив его как плоское кольцо с отождествлением диаметрально противоположных точек внутренней окружности, выполним топологические преобразования (рисунок 135), приводящие к листу Мёбиуса.
Рисунок 135
Дальнейшие построения можно развивать в двух направлениях:
362