
Unlock-Линейная алгебра Сикорская 1
.pdf
например b . Обозначим через λ отношение длин векторов: λ = bа .
Коллинеарные векторы могут быть сонаправленными или противоположно направленными. Тогда проверяя определение произведения вектора на число,
убеждаемся, что а = λb . Согласно свойству 2, векторы а и b линейно зависимы,
что и требовалось доказать.
Замечание. Любые два неколлинеарных между собой вектора образуют линейно независимую систему векторов.
6.Система векторов, состоящая из трех векторов, линейно зависима тогда и только тогда, когда они компланарны.
7.Любые четыре вектора в трехмерном пространстве всегда линейно зависимы.
Вывод: Система векторов, содержащая более чем три вектора в трехмерном пространстве, всегда линейно зависима.
6.4 Базис системы векторов. Координаты вектора относительно базиса
Пусть задана некоторая система векторов S . Число векторов в системе может быть конечным или бесконечным.
Подсистема S′ системы S называется максимально линейно независимой подсистемой, если она удовлетворяет двум условиям:
1S′ - линейно независима;
2При добавлении к системе S′ любого вектора системы S она становится линейно зависимой.
Базисом системы векторов S называется любая максимально линейно независимая подсистема системы S .
Базисом на плоскости назовем два неколлинеарных вектора этой плоскости, взятых в определенном порядке. Обозначение: {e1, e2}.
Базисом в пространстве назовем три некомпланарных вектора, взятых в определенном порядке. Обозначение {e1, e2 , e3}.
В трехмерном пространстве существует бесконечное множество базисов. Рассмотрим в трехмерном пространстве некоторый базис {e1, e2 , e3} и
любой вектор a . Если вектор a |
представлен |
в виде |
линейной |
комбинации |
|
векторов e1, e2 , e3 , то есть a = xe1 + ye2 + ze3 , то говорят, |
что вектор a разложен |
||||
по векторам базиса, а действительные числа x, y, |
z называются коэффициентами |
||||
разложения. |
|
|
|
|
|
Координатами вектора a в базисе {e1, e2 , e3} называются коэффициенты |
|||||
разложения вектора по векторам базиса. Обозначение: a{x, y, z}{e , e |
2 |
, e }. |
|||
|
|
|
1 |
3 |
|
Теорема 6.2 Координаты вектора в фиксированном базисе находятся |
|||||
единственным образом. |
|
a кроме координат x, y, z в |
|||
Доказательство. Допустим, |
что у вектора |
||||
139

базисе {e1, e2 , e3} имеются другие координаты x′, y′, z′. Тогда a = xe1 + ye2 + ze3 = x′e1 + y′e2 + z′e3 .
Следовательно,
(x − x′)e1 + ( y − y′)e2 + (z − z′)e3 = 0 .
По условию векторы базиса {e1, e2 , e3} линейно независимы, а значит, x − x′ = 0, y − y′ = 0, z − z′ = 0 . Поэтому x = x′ , y = y′, z = z′. Других координат у вектора нет.
Свойства координат векторов
1. Координаты суммы (разности) двух векторов, заданных своими
координатами в некотором базисе, равны сумме (разности) соответствующих |
||||||||||||||||
координат |
этих векторов, |
то есть |
если |
a{a1, a2 |
, a3 |
}{e , e |
, e } |
и |
||||||||
|
|
{b1, b2 , b3}{e , e |
, e }, то |
|
|
|
|
|
1 |
2 |
3 |
|
||||
|
b |
|
|
|
|
|
|
|
|
|
||||||
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
||||
|
|
a ± |
|
={a1 ± b1, a2 ± b2 , a3 ± b3}{e1 , e2 , e3 }. |
|
|
|
|
|
|
|
|
||||
|
|
b |
|
|
|
|
|
|
|
|
||||||
|
|
Действительно, рассмотрим векторное пространство V3 . Фиксируем в V3 |
||||||||||||||
базис {e1, e2 , e3}. |
Возьмем два |
произвольных |
вектора |
а и |
|
и |
запишем |
их |
||||||||
b |
||||||||||||||||
разложения в выбранном базисе:
a = a1e1 + a2 e2 + a3e3 , b = b1e1 + b2 e2 + b3e3 .
Используя свойства линейных операций, вычисляем сумму (разность) этих векторов:
a + b = (a1e1 + a2 e2 + a3e3 ) + (b1e1 + b2 e2 + b3e3 ) = = (a1 + b1 )e1 + (a2 + b2 )e2 + (a3 + b3 )e3 .
Получили разложение суммы (разности) векторов в фиксированном базисе. Отсюда заключаем, что координаты аi и bi исходных слагаемых,
соответствующие одному вектору ei в базисе {e1, e2 , e3}, складываются
(вычитаются).
2. Координаты произведения вектора на действительное число равны произведению этого числа на соответствующие координаты вектора в
некотором базисе, а именно, если a{a1, a2 , a3}{e1 , e2 , e3 }, то
b =αa ={αa1, αa2 , αa3}{e1 , e2 , e3 }.
3. Пусть даны векторы a{a1, a2 , a3}{e1 , e2 , e3 } и b{b1, b2 , b3}{e1 , e2 , e3 } и пусть вектор с =αa + βb , тогда на основе предыдущих свойств нетрудно показать,
что вектор с имеет следующие координаты с(αa1 + βb1 ,αa2 + βb2 ,αa3 + βb3 ) .
4. Условие коллинеарности двух векторов, заданных своими координатами в некотором базисе:
Пусть относительно базиса {e1, e2 , e3} даны векторы a{a1, a2 , a3}, b{b1, b2 , b3} и a ||b , тогда по необходимому и достаточному условию b =αa или
140

в координатной форме: |
|
|
|
|
|
|
|
||||
b |
=αa |
|
|
a |
a |
|
|
a |
|||
1 |
1 |
|
2 |
|
|||||||
b |
=αa |
2 |
или |
|
1 |
= |
|
= |
3 |
- условие коллинеарности двух векторов в |
|
|
|
|
|
|
|||||||
2 |
|
|
b1 |
b2 |
|
b3 |
|||||
|
=αa3 |
|
|
||||||||
b3 |
|
|
|
|
|
|
|
|
|
||
координатной форме.
6.5 Ортонормированный базис. Направляющие косинусы вектора. Длина вектора
Рассмотрим в пространстве два неколлинеарнных вектора a, b и отложим их от произвольной точки O пространства (a = OA, b = OB)(рисунок 26).
Рисунок 26
Углом между векторами a и b , если особо не оговорено, будем называть угол AOB , величина которого не превышает π .
Принято угол между сонаправленными векторами считать равным нулю, то есть для любых a и b :
0 ≤ a; b ≤ π .
Два вектора a и b называются ортогональными, если угол между ними равен 90o , т.е. если a b , то a и b ортогональны.
Принято нулевой вектор считать ортогональным с любым другим вектором.
Базис {e1, e2 , e3} трехмерного пространства называется ортонормированным, если выполняются два условия:
1)все векторы этого базиса единичные;
2)векторы базиса попарно ортогональны, то есть e1 e2 , e2 e3, e1 e3 .
Ортонормированный базис в пространстве V3 принято обозначать, с учетом порядка, буквами, {i , j, k }, в V2 - соответственно {i , j} и в V1 -{i }.
Вектора i , j, k называют ортами.
Пусть дан произвольный вектор a = {x, y, z}; будем считать, что a
выходит из начала координат и не лежит ни в одной координатной плоскости. Проведем через точку А плоскости, перпендикулярные координатным осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед, диагональю которого служит отрезок ОА (рисунок 27).
141
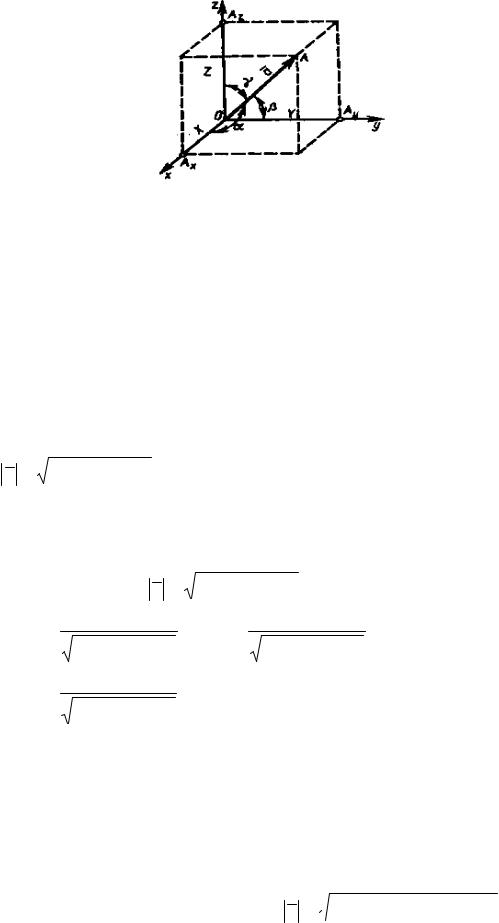
Рисунок 27
Из элементарной геометрии известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его измерений. Следовательно,
|
|
|
ОА |
|
2 = |
|
|
|
ОА |
|
2 + |
|
ОА |
y |
|
2 + |
|
ОА |
|
2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Но |
|
ОА |
|
= |
|
a |
|
, |
|
ОАх |
|
= |
|
x |
|
, |
|
ОАy |
|
|
|
= |
|
y |
|
, |
|
ОАz |
|
= |
|
z |
|
; таким образом, получаем |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
2 = x 2 + y 2 + z 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
a = x2 + y 2 + z 2 . |
|
|
|
|
|
|
|
|
|
|
(6.2) |
||||||||||||||||||||||||||||||||||||||
Формула (6.2) выражает длину произвольного вектора через его
координаты. |
|
|
|
|
|
углы между вектором a и осями координат. Из |
||
Обозначим через α, β, γ |
||||||||
формул прl a = |
|
a |
|
cosϕ и a = |
x2 + y 2 + z 2 |
получаем |
||
|
|
|||||||
cosα = |
|
|
|
x |
, cos β = |
y |
, |
|
|
x2 + y 2 + z 2 |
|
||||||
|
|
|
x2 + y 2 + z 2 |
|
||||
cosα = |
|
|
|
z |
; |
|
|
(6.3) |
|
x2 + y 2 + z 2 |
|
|
|||||
|
|
|
|
|
|
|||
cosα, cos β, cos γ называются направляющими косинусами вектора a .
Возводя в квадрат левую и правую части равенства (6.3) и суммируя полученные результаты, имеем
cos 2 α +cos 2 β + cos 2 γ =1,
т.е. сумма квадратов направляющих косинусов любого вектора равна единице.
Например, вычислим направляющие косинусы вектора а ={12,−15,−16}.
Решение. Найдем длину вектора а = 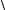 122 + (−15)2 + (−16)2 = 25 . Далее, используя формулу (6.3) имеем
122 + (−15)2 + (−16)2 = 25 . Далее, используя формулу (6.3) имеем
142
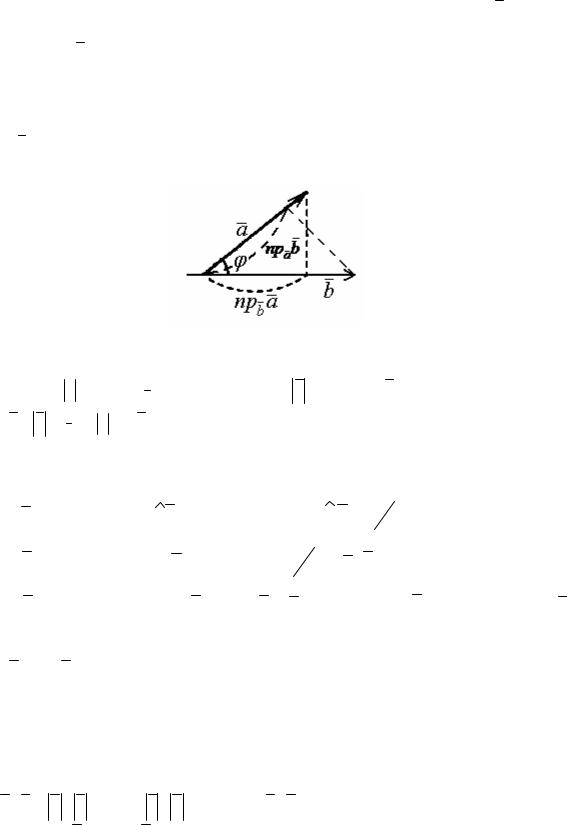
cosα = 1225 , cos β = −1525 , cosγ = −1625 .
6.6 Скалярное произведение векторов и его свойства
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение: а b или (а,b). Итак, по определению
а |
|
= |
|
a |
|
|
|
cosϕ, |
(6.4) |
|
|
|
|
||||||
b |
|
|
b |
||||||
|
|
|
|
|
|
|
|
|
|
где ϕ=(а,b ).
Формуле (6.4) можно придать иной вид.
Рисунок 28 |
|
Так как a cosϕ=прba (рисунок 28), а b cosϕ=прab , то получаем: |
|
ab =b прba = a прab , |
(6.5) |
т.е. скалярное произведение двух векторов равно произведению модуля одного
из них, на проекцию другого на ось, сонаправленную с первым вектором.
Заметим, что
a b > 0 , если cos(a, b )> 0 , то есть 0 ≤ (a, b )<π 2 ; a b < 0 , если cos a , b < 0 , то есть π2 < a , b ≤ π;
a b = 0 , если либо a = 0 , либо b = 0 , либо cos(a, b )= 0 , то есть a b .
Таким образом, скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы ортогональны, то есть
еслиa ≠ 0, b ≠ 0 , но a b = 0 , то a b .
Свойства скалярного произведения векторов
1. a b = b a (коммутативность);
Действительно, свойство непосредственно вытекает из определения скалярного произведения векторов, так как
a b = a b cos ϕ = b a cos(− ϕ)= b a .
2. λa b = λ(a b ) (λ R);
143
Действительно, если b = 0 - нулевой вектор, то обе части доказываемого равенства равны нулю. Если же b ≠ 0 , то, используя выражение скалярного произведения через ортогональную проекцию вектора a на направление вектора b и свойства проекций получаем
(λа)b = b (λa ) = b прb (λa) = λ b прb a = λ(ab ) .
3. (a + b ) c = a c + b c (дистрибутивность относительно сложения
векторов).
Третье свойство предлагаем читателю доказать самостоятельно.
4. Скалярный квадрат вектора есть неотрицательное число, причем, скалярный квадрат вектора равен нулю тогда и только тогда, когда этот вектор нулевой, то есть
a a = a 2 ≥ 0 и a 2 = 0 a = 0.
Из свойства 4 следует, что
a 2 = |
|
a |
|
|
|
a |
|
cos 0 = |
|
a |
|
2 a 2 = |
|
a |
|
2 |
или a = a 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Таким образом, скалярный квадрат вектора равен квадрату его длины. |
|
|||||||||||||||||||
5. |
|
Скалярное |
|
произведение |
векторов |
a ={a1, a2 , a3}{i , j, k |
} |
и |
||||||||||||
b ={b1, b2 , b3}{i , j, k }, заданных в ортонормированном базисе, равно сумме
произведений одноименных координат этих векторов, т.е. |
|
a b = a1b1 + a2b2 + a3b3 . |
(6.6) |
Действительно, так как векторы а и b заданы своими координатами в ортонормированном базисе, то это означает, что имеются разложения
a = a1i + a2 j + a3 k и b = b1i + b2 j + b3 k .
Используя разложения векторов а и b , а также свойства скалярного произведения имеем
ab = (a1i + a2 j + a3 k )(b1i + b2 j + b3 k ) = a1b1i i + a1b2i j + a1b3i k +
|
|
|
|
|
|
+ a2b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ji + a2b2 jj + a2b3 jk + a3b1ki + a3b2 kj + a3b3 kk = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + a |
|
b |
|
|
2 + a |
|
|
|
2 |
= a b + a |
|
b |
|
+ a |
|
b . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
= a b i |
2 |
2 |
j |
3 |
b k |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
Окончательный ответ получен с учетом того, что ортонормированность |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
базиса |
{i |
, |
|
|
|
} |
|
|
|
|
означает |
выполнение |
|
равенств |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
, k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
j |
|
|
|
|
|
i j = i |
k = jk = 0 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
=1.Таким образом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
i |
i = jj = kk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
a b = a1b1 + a2b2 + a3b3 .
6. Укажем еще одну формулу, вытекающую из определения скалярного произведения и формул для нахождения длин векторов, координаты которых известны в ортонормированном базисе.
Пусть a ={a1, a2 , a3}{i , j, k } и b ={b1, b2 , b3}{i , j, k }. Так как a b = a b cosϕ , то
144

|
|
|
|
|
|
|
|
|
b |
|
|
|
|
a1b1 + a2b2 + a3b3 |
|
||
cos ϕ = |
a |
или cosϕ = |
(6.7) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
a12 + a22 + a32 b12 + b22 + b32 |
|||||||
|
|
|
|
|
|
|
|
b |
|
|
|||||||
|
|
|
|
|
|
||||||||||||
|
a |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Взаключении этого параграфа приведем пример применения определения
исвойств скалярного произведения при решении следующей задачи:
Найти (a, b ) , если a = m − 3n , b = 2m + 2n, m = 3, n = 3,(m,n) =π .
Решение.
(a, b ) = (m − 3n, 2m + 2n) = (m,2m + 2n) + (−3n,2m + 2n) = (m,2m) + (m,2n) + + (−3n,2m) + (−3n,2n) = 2(m, m) + 2(m, n) − 6(n, m) − 6(n, n) = 2 m 2 − 6 n 2 − − 4 m
 n cos(m, n) = 2 32 − 6 32 − 4 3 3 cosπ =18 − 54 + 36 = 0.
n cos(m, n) = 2 32 − 6 32 − 4 3 3 cosπ =18 − 54 + 36 = 0.
Итак, (a, b ) = 0 , то есть векторы a и b ортогональны.
6.7 Векторное произведение двух векторов и его свойства
Три некомпланарных вектора a, b , c взятых в указанном порядке, образуют правую тройку, если из конца третьего вектора с кратчайший поворот
от первого вектора a ко второму вектору b виден совершающимся против часовой стрелки. В противном случае - тройка левая (рисунок 29).
|
|
|
с |
|
|
правая тройка |
|
|
|
|
|
|
|
левая тройка |
||
|
|
|
|
|
|
|
с |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
a |
|
|
b |
|
|
|
|
a |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рисунок 29 |
|
|
|
|
||||
Векторным |
произведением |
двух неколлинеарных |
векторов a и |
|
||||||||||||
b |
||||||||||||||||
называется вектор, численно равный площади параллелограмма, построенного на векторах a , b ; направленный перпендикулярно плоскости перемножаемых векторов и образующих с ними правую тройку.
Векторное произведение векторов a и b обозначается a ×b или [a,b ]
Рисунок 30
Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j, k (рисунок 31)
145
[i , j]= k , [j, k ]= i , [k , i ]= j .
Рисунок 31
Свойства векторного произведения векторов
1. Модуль векторного произведения двух векторов равен произведению длин этих векторов на синус угла между ними.
Рассмотрим два неколлинеарных вектора a, b и отложим их от произвольной точки O (рисунок 32).
Рисунок 32
Построим параллелограмм на этих векторах как на сторонах. Найдем площадь параллелограмма OACB :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
SOACB = OA OB sin AOB = |
a |
|
b |
|
sin a, b . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку, модуль векторного произведения двух неколлинеарных векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах, то
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
[a , b ] |
= |
a |
|
b |
sin a,b . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нуль-вектору, то есть
[a, b ]= 0 .
|
|
|
|
|
Действительно, если |
a и |
|
коллинеарны, то sinϕ = 0 . Следовательно, |
||||||||||
|
|
|
|
b |
||||||||||||||
|
[a, |
|
] |
|
= |
|
a |
|
|
|
|
|
sin ϕ = 0 , т.е. |
длина вектора [a, |
|
] равна нулю, а значит, вектор |
||
|
b |
|
|
|
|
b |
|
b |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a, b ]является нуль-вектором.
3. Векторное произведение двух неколлинеарных векторов антикоммутативно, то есть
146

[a,b ]= −[b ,a].
Действительно, если векторы a и b коллинеарны, то свойство очевидно. Пусть a и b неколлинеарны. Из определения векторного произведения следует, что векторы [a, b ] и [b , a ] имеют одинаковые длины (длина векторного произведения не зависит от порядка сомножителей), коллинеарны (они перпендикулярны одной и той же плоскости в которой лежат векторы a и b ), но
направлены противоположно, так как |
|
|
|
если, например, векторы a, b , [a, b ] |
||||||||||||||||||||||||
образуют правую тройку, то векторы a, |
|
|
|
, [ |
|
, |
|
]. Следовательно. [a, |
|
]= −[ |
|
,a]. |
||||||||||||||||
|
b |
b |
a |
b |
b |
|||||||||||||||||||||||
4.Числовой множитель можно выносить за знак векторного |
||||||||||||||||||||||||||||
произведения, то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
[λ |
|
, |
|
]= λ[ |
|
, |
|
] |
(λ R) или [ |
|
,α |
|
]= α[ |
|
, |
|
] (α R). |
|||||||||||
|
b |
b |
b |
b |
||||||||||||||||||||||||
a |
a |
a |
a |
|||||||||||||||||||||||||
5. Векторное |
произведение векторов дистрибутивно относительно |
|||||||||||||||||||||||||||
операции сложения векторов, то есть
[a + b , c ]= [a, c ] + [b , c ].
Доказательство 3 и 4 свойств предлагаем читателю выполнить самостоятельно.
6.Выражение векторного произведения через координаты.
Результаты векторного произведения базисных векторов занесем в таблицу:
|
|
|
|
|
|
i |
|
|
j |
k |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
||||||
|
|
i |
|
|
|
0 |
|
|
|
k |
|
|
j |
|
|
|||||||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
j |
|
k |
|
|
|
0 |
|
|
|
i |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
− i |
|
|
|
|
|
|
||||||||||
|
k |
|
|
|
j |
|
0 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 33
Чтобы не ошибиться со знаком, удобно пользоваться схемой (рисунок 33): если направление кратчайшего пути от первого вектора ко второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает – третий вектор берется со знаком «минус».
Пусть даны два векторы a = a1i + a2 j + a3 k и b = b1i + b2 j + b3 k . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно
свойствам векторного произведения):
[a, |
|
]= [(a1i |
+ a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ b2 |
|
|
|
|
|
|
|
|
|
|
|
)]= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
b |
+ a3 k |
+ b3 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
j |
), (b1i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= a1b1 [i |
|
|
|
]+ a1b2 |
[i |
, |
|
]+ a1b3 [i |
|
|
|
|
|
]+ a2b1 [ |
|
|
|
|
|
]+ a2b2 [ |
|
, |
|
|
|
]+ a2b3 [ |
|
|
|
|
|
]+ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
, k |
, k |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, i |
j |
j |
, i |
j |
j |
j |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+ a3b1 [k |
|
|
]+ a3b2 [k |
, |
|
]+ a3b3 [k |
|
|
]= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
, i |
j |
, k |
0 |
|
+ a1b2 k |
− a1b3 |
j |
− a2b1k + |
0 |
+ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
+ a3b1 |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+ a2b3i |
j |
− a3b2i |
|
= (a2b3 − a3b2 )i |
− (a1b3 − a3b1 ) j + |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+ (a b |
|
|
− a |
|
|
|
|
|
|
a2 |
|
|
a3 |
|
|
|
|
|
a1 |
a3 |
|
|
|
+ |
|
a1 |
|
a2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
b )k |
= |
|
|
|
|
− |
|
|
k |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
|
|
|
i |
|
j |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
b2 |
|
|
b3 |
|
|
|
|
|
|
|
|
b1 |
b3 |
|
|
|
|
|
|
|
|
|
|
b1 |
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Полученную формулу можно записать еще короче:
147

|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a , |
|
]= |
i |
|
|
j |
k |
|
|
||||
|
a1 |
a2 |
a3 |
, |
(6.8) |
||||||||
b |
|||||||||||||
|
|
|
b1 |
b2 |
b3 |
|
|
||||||
так как правая часть предыдущего равенства соответствует разложению определителя третьего порядка по элементам первой строки.
Например, вычислим площадь параллелограмма, построенного на векторах a ={6,3,−2},b ={3,−2,6}.
Решение. Находим векторное произведение векторов a, b , используя (6.8):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a, |
|
]= |
i |
|
|
j |
k |
|
|
|
3 |
− 2 |
|
|
|
6 |
− 2 |
|
|
|
6 |
3 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
6 |
3 − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
b |
+ k |
|
|||||||||||||||||||||||||||||||
= i |
|
− 2 |
6 |
− j |
3 |
6 |
|
3 |
− 2 |
=14i − 42 j − 21k . |
|||||||||||||||||||||||
|
|
|
3 |
− 2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как модуль векторного произведения двух векторов равен площади построенного на них параллелограмма, то
Sпар = [a, b ] =  142 + (−42)2 + (−21) 2 = 49 (кв.ед.).
142 + (−42)2 + (−21) 2 = 49 (кв.ед.).
Таким образом, площадь искомого параллелограмма равна 49 квадратным единицам.
6.8 Смешанное произведение трех векторов и его свойства
Смешанным произведением трех векторов a, b , c называется число,
обозначаемое (a, |
|
|
, c ) и равное скалярному |
произведению вектора a |
|
|
на |
||||||||||||||||||||
b |
|||||||||||||||||||||||||||
векторное произведение векторов |
|
|
|
и c , то есть |
|
|
|
|
|
|
|
|
|
||||||||||||||
b |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
( |
|
, |
|
, |
|
)= |
|
[ |
|
, |
|
]. |
|
|
(6.9) |
||||||||||||
|
b |
b |
|||||||||||||||||||||||||
a |
c |
a |
c |
||||||||||||||||||||||||
Пусть относительно ортонормированного базиса {i |
, |
|
|
|
} векторы a, |
|
|
, c |
|||||||||||||||||||
|
, k |
b |
|||||||||||||||||||||||||
j |
|||||||||||||||||||||||||||
имеют координаты a ={a1, a2 , a3}, |
|
={b1, b2 , b3}, |
c ={c1, c2 , c3}. |
|
|
|
|||||||||||||||||||||
b |
|
|
|
||||||||||||||||||||||||
Смешанное произведение трех векторов, заданных своими координатами в ортонормированном базисе, равно определителю третьего порядка, составленному из их координат, то есть
|
|
|
|
a1 |
a2 |
a3 |
|
(a , |
|
, |
c |
)= b1 |
b2 |
b3 . |
(6.10) |
b |
c1 c2 c3
Справедливость (6.10) следует из координатного представления скалярного произведения векторов и правила нахождения координат векторного произведения. (Предлагаем доказательство формулы (6.10) выполнить читателю самостоятельно.)
Теорема 6.2. Смешанное произведение векторов равно нулю (a, b , c )= 0 тогда и только тогда, когда либо векторы a, b , c компланарны, либо хотя бы один вектор нулевой.
148
