
Unlock-Линейная алгебра Сикорская 1
.pdf
7.4 Уравнение линии на плоскости
Уравнением линии на плоскости в заданной системе координат Oxy
называется уравнение с двумя неизвестнымиF(x, y) = 0 , которому удовлетворяют
координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты точек, не лежащих на ней.
Входящие в уравнение F(x, y) = 0 координаты x и y произвольной линии
называются текущими координатами.
Для составления уравнения линии следует взять на ней произвольную точку и, исходя из свойств линии, установить зависимость между координатами точек.
Понятие уравнения линии дает возможность решать геометрические задачи алгебраическими методами. Например, задача нахождения точек
пересечения линий, определяемых уравнениями x + y = 0, x 2 + y 2 =1, сводится к
алгебраической задаче решения системы этих уравнений. Рассмотрим примеры линий:
1 x − y = 0 . Переписав это уравнение в виде x = y , заключаем что
множество точек, координаты которых удовлетворяют этому уравнению лежат на биссектрисе I – III координатных углов.
2 |
x 2 − y 2 = 0 . |
Представив уравнение |
в виде (x − y)(x + y) = 0 , что |
|||
равносильно |
x − y = 0, |
или |
x = y, |
, получим x 2 |
− y 2 = 0 - уравнение биссектрис |
|
|
|
|||||
|
|
x + y = 0. |
|
x = −y. |
|
|
всех координатных углов (рисунок 43)
Рисунок 43
3 x 2 + y 2 = 0 . Этому уравнению удовлетворяет лишь точка (0,0) . В данном случае говорят, что уравнение x 2 + y 2 = 0 определяет вырожденную линию.
4 x 2 + y 2 +1 = 0 . Перепишем уравнение в видеx 2 + y 2 = −1, которое означает что нет ни одной точки ему удовлетворяющей. Таким образом,
уравнение |
x 2 + y 2 +1 = 0 никакого |
геометрического |
образа |
на плоскости не |
определяет. |
Линия на плоскости может определятся уравнением вида F (ρ,ϕ) = 0 , |
|||
5 |
||||
где (ρ,ϕ) |
- полярные координаты |
точки. Например, |
пусть |
задано уравнение |
159

ρ = a cosϕ , где a - положительной число, переменныеρ,ϕ - полярные координаты. Определим линию задаваемую этим уравнением. Пусть M (ρ,ϕ) - точка удовлетворяющая этому уравнению и точка А с координатами (a,0) - некоторая фиксированная точка (рисунок 44)
Рисунок 44
Если ρ = a cosϕ , где 0 <ϕ <π / 2 , то угол ОМА - прямой (по свойству
прямоугольного треугольника – гипотенуза есть произведение прилежащего катета на косинус угла между ними), но если угол ОМА прямой, то треугольник ОМА является вписанным в окружность (опирающимся на диаметр ОА). Следовательно, множество точек, полярные координаты которых удовлетворяют уравнению ρ = a cosϕ есть окружность с диаметром a .
Итак, по заданному уравнению мы определили в примерах 1-5 линию как геометрическое множество точек ему удовлетворяющих.
Рассмотрим обратную задачу.
Например, выведем уравнение (в заданной прямоугольной системе координат) множества точек, каждая из которых отстоит от точки С(a, b) на
расстоянии R .
Решение. Исходя из условия определяем, что наша задача вывести уравнение окружности радиуса R с центром в точке С(a, b) (рисунок 45).
Рисунок 45
Расстояние от произвольной точки M (x, y) до точки С(a, b) вычисляется по формуле
МС = (x − a)2 + ( y − b)2
160

Если точка M (x, y) лежит на окружности, то МС = R . Таким образом,
R = (x − a)2 + ( y − b)2
или |
|
|
|
|
|
R 2 = (x − a) 2 + ( y − b)2 |
(7.10) |
||||
Если же точка, например, M1 (x, y) не лежит на окружности, |
то |
|
М1С |
|
≠ R |
|
|
||||
или М1С2 ≠ R 2 , то есть координаты точки М не удовлетворяют уравнению |
|||||
(7.10). Таким образом, искомое уравнение окружности имеет вид |
|
|
|
|
|
R 2 = (x − a) 2 + ( y − b) 2 |
|
|
|
|
|
В частности, если a = 0, b = 0 , то есть центр окружности |
совпадает с |
||||
началом координат, то есть |
|
|
|
|
|
x 2 + y 2 = R 2 . |
|
|
|
|
|
Если в уравнение линии переменные входят только в первой степени, то такая линия называется линией первого порядка. К линиям второго порядка
относятся такие линии, уравнения которых в прямоугольной системе координат являются уравнениями второй степени. К линиям первого порядка относятся прямые, второго порядка – эллипс, гипербола, парабола.
Линию на плоскости также можно задать при помощи уравнений:
x = x(t),
y = y(t),
где x и y – координаты произвольной точки M(x, y), лежащей на данной линии, а t
– переменная, называемая параметром. Параметр t определяет положение точки (x,y) на плоскости.
Например, если x=t+1, y=t², то значению параметра, равному двум, соответствует на плоскости точка (3,4), т.к. x=2+1=3, y=2²=4.
Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линий называется
параметрическим, а уравнения – параметрическими уравнениями линий.
Чтобы перейти от параметрических уравнений к уравнениям вида F(x,y)=0, надо каким-либо способом из двух заданных уравнений исключить параметр t.
Например, из уравнений x = t |
, путём подстановки t = x во второе уравнение, |
y = t 2 |
|
легко получить уравнение у = х2 ; или уравнение вида у − х2 = 0 , т.е.вида
F(x,y)=0. Однако заметим, такой переход не всегда целесообразен и не всегда возможен.
161
7.5 Линии первого порядка на плоскости
1 Уравнение прямой с угловым коэффициентом
Пусть дана некоторая прямая с заданным углом наклона к оси Ox угол α , причем 0 ≤α <π (рисунок 46)
Тангенс угла наклона прямой к оси Ох называется угловым
коэффициентом этой прямой и обозначается k |
|
k = tqα . |
(7.11) |
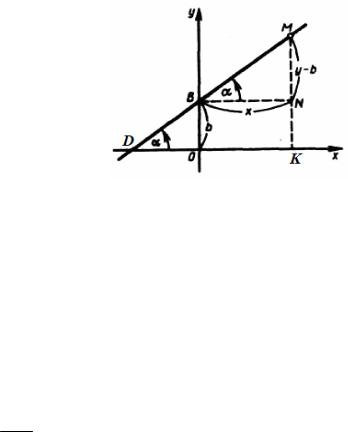
Рисунок 46
Выведем уравнение прямой, если известны ее угловой коэффициент k и величина b- длина отрезка ОВ отсекаемого данной прямой на оси Оу (рисунок 46).
Пусть M (x, y) - произвольная точка искомой прямой. Выполним
построение – из точки М проведем прямую параллельную оси Оу, а из точки В - параллельную оси Ох. Полученный, таким образом, треугольник BNM - прямоугольный, углы MBN и MDK равны как соответственные. По определению тангенса острого угла прямоугольного треугольника, имеем
tqα = MNBN ,
но MN=KM-KN=KM-OB=y-b, а BN=x и k = tqα (по условию)
Таким образом, имеем
k = |
y − b |
|
|
x |
|
||
|
|
||
или y − b = kx |
|
||
y = kx +b . |
(7.12) |
||
Уравнение (7.12) называется уравнением прямой с угловым |
|||
коэффициентом. |
|
||
Если k = 0 |
(т.е. tqα = 0 α = 0 ), то прямая параллельна оси Ox и имеет |
||
уравнение y = b .
Таким образом, любая прямая не перпендикулярная оси Ox имеет уравнение вида (7.12). Верно и обратное: любое уравнение вида (7.12) определяет прямую, которая имеет угловой коэффициент k и отсекает на оси Oy отрезок величиной b.
162
2 Уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом
Пусть требуется составить уравнение прямой, зная одну ее точку M1 (x1 , y1 ) и угловой коэффициент k . Запишем уравнение искомой прямой в виде
(7.12) y = kx + b , где b пока неизвестное число. Так как прямая проходит через точку M1 (x1 , y1 ) , то координаты этой точки удовлетворяют уравнению (7.12), то
есть y1 = kx1 + b , откуда находим b = y1 − kx1 |
и подставляем в исходное |
уравнение: |
|
y = kx + ( y1 − kx1 ) |
|
или |
|
y − y1 = k( x − x1 ), |
(7.13) |
- уравнение прямой проходящей через точку M1 (x1 , y1 ) имеющей угловой
коэффициент k .
Например, составим уравнение прямой, проходящей через точку А(2,−1) и образующей с осью Ох угол 450 .
Решение. Так как k = tg 450 =1, то, использовав уравнение (7.13), получим y − (−1) =1(x − 2) , или x − y = 3.
Итак, y = x − 3 - уравнение искомой прямой.
3 Уравнение прямой, проходящей через две заданные точки
Пусть M1 (x1 , y1 ) и M 2 (x2 , y2 ) - две заданные точки через которые проходит искомая прямая, тогда поскольку точка M1 (x1 , y1 ) принадлежит искомой прямой, то на основе формулы (7.13) имеем
|
y − y1 = k(x − x1 ) . |
(7.14) |
||||||||||||||
Но уравнению (7.14) удовлетворяет и точка M 2 (x2 , y2 ) , следовательно |
||||||||||||||||
|
y2 − y1 = k(x2 − x1 ) . |
|
||||||||||||||
Откуда находим k |
|
|||||||||||||||
k = |
|
y2 − y1 |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
2 |
|
− x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
Таким |
|
|
образом, уравнение искомой |
прямой, проходящей через точки |
||||||||||||
M1 (x1 , y1 ) и M 2 (x2 , y2 ) , имеет вид |
|
|||||||||||||||
|
y − y = |
y2 − y1 |
(x − x ) |
|
||||||||||||
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
x |
|
|
|
1 |
|
||||
или |
|
|
|
|
|
|
|
2 − x1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y − y1 |
|
= |
x − x1 |
. |
(7.15) |
||||||||||
|
|
|
|
|||||||||||||
|
y |
2 |
− y |
2 |
|
|
x |
2 |
− x |
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
- уравнение прямой, проходящей через две заданные точки.
163
4 Угол между двумя прямыми |
|
|
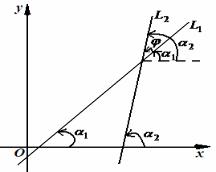
Рассмотри две прямые L1 : y = k1 x + b1 , |
где |
k1 = tgα1 и L2 : y = k2 x + b2 , |
где k2 = tgα2 . Поставим задачу: найти угол |
ϕ |
между прямыми L1 , L2 . Из |
геометрических соображений устанавливаем зависимость между углами α1 , α2 и ϕ (рисунок 47)
Рисунок 47
α2 = α1 + ϕ ϕ =α2 −α1 . |
|
|
|
|
|
|
|
|
||||||||||||||||
Следовательно, |
|
|
tgα2 − tgα1 |
|
|
|
|
|
|
|
||||||||||||||
tgϕ = tg(α2 − α1 ) = |
. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
Таким образом, |
|
1 + tgα1tgα2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
tgϕ = |
|
|
k2 − k1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.16) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 + k k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Формула (7.16) определяет один из углов между прямыми L1 , L2 , другой |
||||||||||||||||||||||||
угол равен π −ϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Например, |
|
найдем |
|
угол |
между |
прямыми, |
заданными |
уравнениями |
||||||||||||||||
y = 2x −1 и y = x + 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Очевидно k1 = 2, k2 =1, по формуле (7.16) находим угол между прямыми: |
||||||||||||||||||||||||
tgϕ = |
|
|
1 − 2 |
|
= − |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
1 +1 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||
Таким |
образом, |
тангенс |
одного |
из углов |
равен − |
, |
а сам |
угол |
||||||||||||||||
|
||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ϕ = arctg |
− |
|
|
|
=π − arctg |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5 Условие параллельности и перпендикулярности двух прямых |
|
|||||||||||||||||||||||
Если прямые L1 , |
L2 |
параллельны, |
то ϕ = 0 , |
и tgϕ = 0 . В этом случае |
||||||||||||||||||||
числитель формулы (7.16) равен 0, то есть k2 −k1 = 0 или |
|
|
||||||||||||||||||||||
k1 = k2 - условие параллельности прямых. |
|
|
|
ϕ =π / 2 , |
|
|||||||||||||||||||
Если |
|
|
|
прямые |
L1 , L2 |
перпендикулярны, |
то есть |
то |
||||||||||||||||
164
|
|
π |
|
π |
|
|
|
|
1 |
|
||
α2 |
= |
|
+ α1 tgα2 |
= tg |
|
+ α1 |
|
tgα2 |
= −сtgα1 tgα2 = − |
|
, то есть |
|
2 |
2 |
tgα1 |
||||||||||
|
|
|
|
|
|
|
|
|
||||
k2 =− 1 - условие перпендикулярности прямых. k1
6 Общее уравнение прямой
Теорема 7.1 В прямоугольной системе координат любая прямая задается уравнением первой степени
Ax+By+C =0 |
(7.17) |
и обратно, уравнение (7.17) при произвольных коэффициентах А, В, С определяет некоторую прямую в прямоугольной системе координат Оху.
Доказательство. Докажем первое утверждение. Если прямая не перпендикулярна оси Ох, то она имеет уравнение y =kx +b, которое имеет вид (7.17) при A =k, B =−1,C =b. Если прямая перпендикулярна оси Ох, то все ее точки
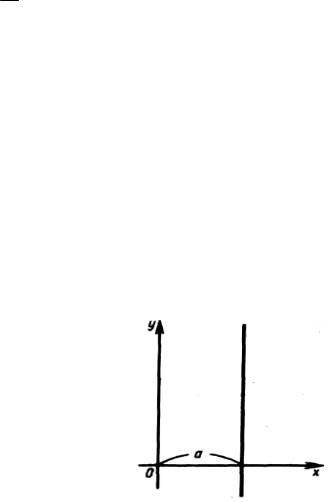
имеют одинаковые абсциссы, равные а – величине отрезка, отсекаемого на оси Ох (рисунок 48)
Рисунок 48
Уравнение этой прямой имеет вид x =a, то есть является уравнением первой степени вида (7.17), где A=1, B =0,C =−a. Таким образом, первое
утверждение доказано.
Докажем обратное утверждение. Пусть дано уравнение (7.17), причем хотя
бы один из коэффициентов |
A, B не равен нулю. Если B ≠0, то (7.17) можно |
|||||||||||||||
записать в виде |
|
|
|
|
|
|
|
|
|
|
||||||
y =− |
A |
x − |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
B B |
|
|
|
|
|
|
|
|
|
|
|||||
Полагая k =− |
A |
|
, b =− |
C |
|
, получаем уравнение y =kx +b. |
|
|
|
|
||||||
B |
B |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
C |
|
|
C |
|
|
||||
Если B =0, A≠0, то (7.17) принимает вид x =− |
. Обозначая |
− |
|
через а, |
||||||||||||
|
A |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|||
получим x =a, то есть уравнение прямой, перпендикулярной оси Ох, что и требовалось доказать.
165
Уравнение вида Ax+By+C =0 называется общим уравнением прямой.
7 Неполное уравнение первой степени. Уравнение прямой «в
отрезках» |
|
Ax+ By+C =0 |
является |
|
Рассмотрим три частных случая, когда уравнение |
||||
неполным, т.е. какой-то из коэффициентов равен нулю. |
|
|
||
1) |
C =0; уравнение имеет вид |
Ax+ By =0 и |
определяет |
прямую, |
проходящую через начало координат. |
|
|
|
|
2) |
B =0 (А≠0); уравнение имеет |
вид Ax+C =0 |
и определяет |
прямую, |
параллельную оси Оу. Как было показано в теореме 7.1, это уравнение приводится к виду x =а, где а=−С/ А, а - величина отрезка, отсекаемого прямой на оси Ох (рисунок 48). В частности, если а=0, то прямая совпадает с осью Оу. Таким образом, уравнение x =0 определяет ось ординат.
3) A=0, (В≠0); уравнение имеет вид By+C =0 и определяет прямую,
параллельную оси Ох. Этот факт устанавливается аналогично предыдущему случаю. Если положить −С/ В=b, то уравнение принимает вид y =b, где b -
величина отрезка, отсекаемого прямой на оси Оу (рисунок 49). В частности, если b =0, то прямая совпадает с осью Ох. Таким образом, уравнение y =0 определяет
ось абсцисс.
Рисунок 49
Пусть теперь дано уравнение Ax+ By+C =0 при условии, что ни один из коэффициентов А, В, С не равен нулю. Преобразуем его к виду
|
|
|
x |
|
|
+ |
y |
|
=1. |
|
|
−C / A |
−C / B |
||||||||
|
|
|
||||||||
Вводя обозначения a =−C / A, b =−C / B, получаем |
||||||||||
|
x |
|
+ |
y |
=1. |
|
(7.18) |
|||
|
a |
b |
|
|||||||
|
|
|
|
|
|
|
|
|||
Уравнение (7.18) называется уравнением прямой «в отрезках». Числа a, b
являются величинами отрезков, отсекаемого прямой на осях координат. Эта форма уравнения удобна для геометрического построения прямой.
Например, составим для заданной уравнением 5x + 3y −15 = 0 прямой
уравнение «в отрезках» и построим эту прямую. Для данной заданной прямой, имеем
166

A=5, B =3,C =−15 a =−CA =155 =3,
b =−CB =−153 =−5.
Таким образом, уравнение заданной прямой «в отрезках» имеет вид
3x + −y5 =1.
Чтобы построить эту прямую, отложим на осях координат Ох и Оу отрезки a =3, b =5 и проведем прямую через точки M1(−5,0), M2(0,3) (рисунок 50).
Рисунок 50
8 Уравнение прямой в полярных координатах. Нормальное уравнение прямой
Пусть дана некоторая прямая L. Проведем через начало координат прямую n, перпендикулярную данной, и назовем ее нормалью к прямой L. Буквой N отметим точку, в которой нормаль пересекает прямую L (рисунок 51). На нормали введем направление от точки O к точке N. Таким образом, нормаль станет осью.
Обозначим через α угол, на который нужно повернуть против часовой стрелки ось Ох до совмещения ее положительного направления с направлением нормали, через p - длину отрезка ON.
Рисунок 51
Тем самым, 0 ≤α < 2π, p ≥ 0 . Выведем уравнение данной прямой, считая известными числа α и p. Для этого возьмем на прямой произвольную точку М с
167
полярными координатами (ρ,ϕ) , где О – полюс, Ох – полярная ось. Если точки О и N не совпадают, то из прямоугольного треугольника ONM имеем
p =ρcos(ϕ −α) =ρ(cosαcosϕ +sinαsinϕ). |
|
Это равенство можно переписать в виде |
|
ρcosαcosϕ+ρsinαsinϕ− p =0 |
(7.19) |
Так как точки, не лежащие на данной прямой L, не удовлетворяют уравнению (7.19), то (7.19) - уравнение прямой L в полярных координатах.
Но в силу формул, связывающих прямоугольные и полярные координаты, имеем: ρcosϕ = х, ρsinϕ = y. Таким образом, уравнение (7.19) в прямоугольной
системе координат примет вид |
|
xcosα+ ysinα− p =0. |
(7.20) |
Если точки О и N совпадают, то прямая L проходит через начало координат и p =0.
В этом случае, очевидно, для любой точки М прямой L выполняется равенство cos(ϕ −α) =0. Умножая его на ρ , получаем ρcos(ϕ −α) =0, откуда
ρcosαcosϕ + ρsinαsinϕ =0 или xcosα+ ysinα=0.
Таким образом, и в этом случае уравнение прямой можно представить в виде (7.20).
Уравнение (7.20) называется нормальным уравнением прямой L.
9 Расстояние от точки до прямой
С помощью нормального уравнения прямой можно определить расстояние от данной точки плоскости до прямой.
Пусть L - прямая, заданная нормальным уравнением:
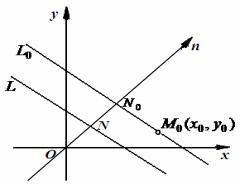
xcosα+ ysinα− p =0 и пусть M0 (x0 , y0 ) - точка, не лежащая на этой прямой. Требуется найти расстояние d от точки M0 до прямой L.
Через точку M0 проведем прямую L0 параллельно прямой L. Пусть N 0 - точка пересечения L0 с нормалью, p0 - длина отрезка ON 0 (рисунок 52).
|
|
Рисунок 52 |
|
Если точки |
N и |
N 0 лежат по одну сторону от точки О, то нормальное |
|
уравнение прямой |
L0 |
имеет вид xcosα+ ysinα− p0 =0. Так как |
точка |
M0 (x0 , y0 ) L0, то |
x0 cosα+ y0 sinα− p0 =0, откуда x0 cosα+ y0 sinα= p0. В |
этом |
|
168
