Unlock-Линейная алгебра Сикорская 1
.pdf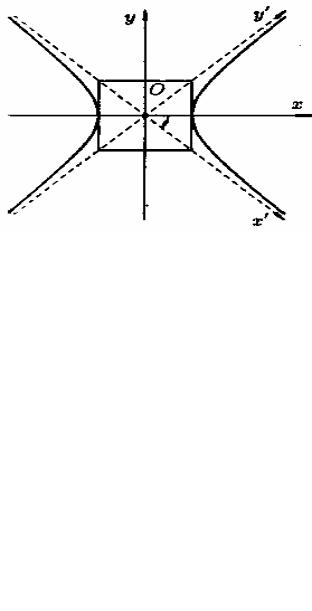
Рисунок 62
Уравнение равносторонней гиперболы, асимптотами которой служат оси координат.
Гипербола (7.34) называется равносторонней, если ее полуоси равны (а= b). Ее каноническое уравнение имеет вид
х2 − у2 =а2 . |
(7.36) |
|
|
|
|
|
|
|
Рисунок 63
Асимптоты равносторонней гиперболы имеют уравнения у = х и у=-х и, следовательно, являются биссектрисами координатных углов.
Рассмотрим уравнение этой гиперболы в новой системе координат Ох'у'
(рисунок 63), полученной из старой поворотом осей координат на угол |
α =− |
π . |
|||
Используем формулы поворота осей координат: |
|
4 |
|||
|
|
||||
|
′ |
′ |
sinα, |
|
|
x = x cosα − y |
(7.37) |
||||
|
′ |
′ |
cosα. |
||
y = x sinα + y |
|
|
|||
Подставляем значения х и у в уравнение (7.36):
179

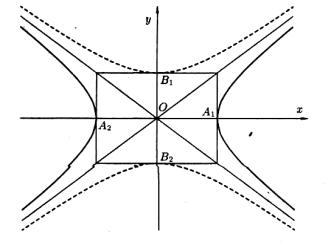
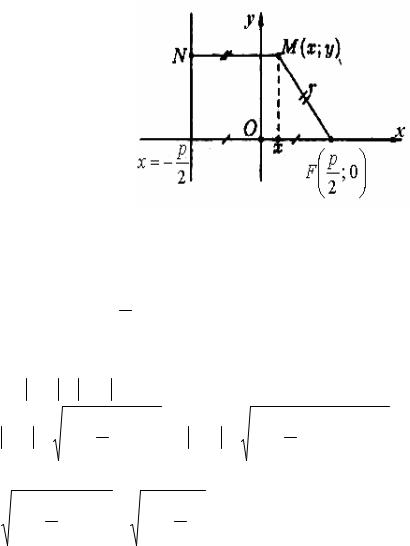
Рисунок 66
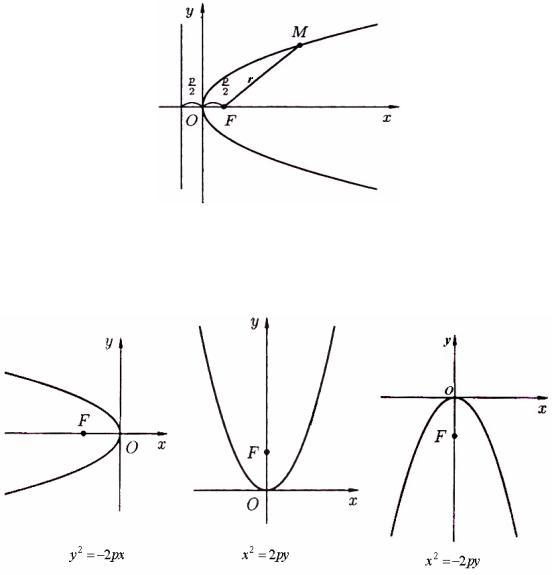
В выбранной системе фокус F имеет координаты (p / 2,0), а у равнение директрисы имеет x + 2p =0.
Пусть М(х,у) — произвольная точка параболы. Соединим точку М с F. Проведем отрезок MN перпендикулярно директрисе. Согласно определению параболы MF = MN . По формуле расстояния между двумя точками находим:
|
|
p 2 |
|
, а |
MN = |
|
p 2 |
|||
MF = x − |
+ y2 |
x + |
+( y − y )2 . |
|||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
Следовательно, |
|
|
|
|
|
|
|
|||
|
p 2 |
|
|
+ |
p 2 |
|
|
|||
x − |
+ y2 = |
x |
2 |
. |
|
|
||||
|
2 |
|
|
|
|
|
|
|||
Возведя обе части уравнения в квадрат, получаем |
||||||||||
x2 − px+ |
p2 |
+ y2 |
= x2 + px+ |
p2 |
, |
|
||||
|
|
|
||||||||
т.е. |
4 |
|
|
|
|
4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y2 =2px |
|
|
|
|
|
|
|
(7.39) |
||
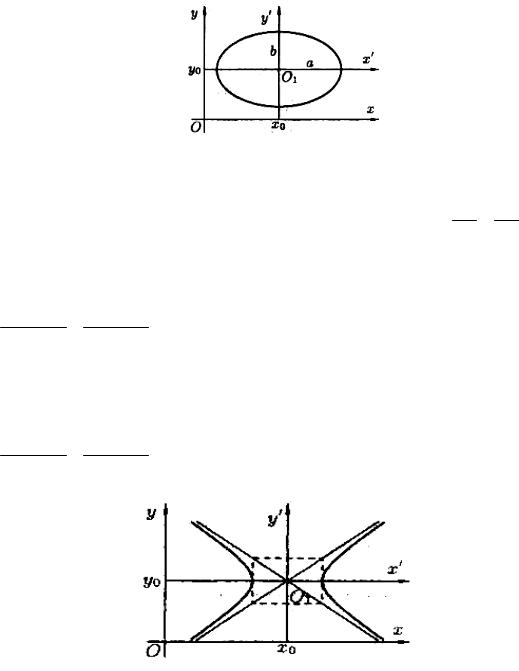
Уравнение (7.39) называется каноническим уравнением параболы.
Например, определим параметр параболы y2 =2px, проходящей через точку А(2,4) .
Для этого подставим в уравнение параболы вместо текущих координат координаты точки А(2,4) и получим
42 =2p2 16=4p p =4,
Т.е. искомый параметр равен четырем.
Исследование формы параболы по ее уравнению
1 В уравнении (7.39) переменная у входит в четной степени, значит, парабола симметрична относительно оси Ox; ocь Ох является осью симметрии
182


Общее уравнение второго порядка
Рассмотрим теперь общее уравнение второй степени с двумя неизвестными (запишем его в более удобной форме):
Ax2 +2Bxy+Cy2 +2Dx+2Ey+ F =0. |
(7.45) |
Оно отличается от уравнения (7.42) присутствием члена с произведением координат (В≠0) . Докажем, что можно, путем поворота координатных осей на
угол α, преобразовать это уравнение, таким образом, чтобы в нем член с произведением координат отсутствовал.
Действительно, используя формулы поворота осей
x = x′cosα − y′sinα,y = x′sinα + y′cosα.
Выразим старые координаты через новые:
′ |
|
|
|
|
′ |
2 |
+ |
′ |
′ |
′ |
|
|
′ |
′ |
′ |
|
2 |
|
A(x cosα − y sinα) |
|
2B(x cosα − y sinα)(x sinα + y cosα) +C(x sinα + y cosα) |
|
|||||||||||||||
|
′ |
|
|
′ |
|
|
′ |
′ |
|
+F =0. |
|
|
|
|
||||
+2D(x cosα − y sinα) +2Е(x sinα |
+ y cosα) |
|
|
|
|
|||||||||||||
Выберем угол |
α |
так, чтобы коэффициент при |
′ |
y |
′ |
обратился в нуль, т.е. чтобы |
||||||||||||
|
x |
|
||||||||||||||||
выполнялось равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
−2Acosαsinα +2B(cos2 α −sin2 α) +2Csinαcosα =0, |
|
|
|
|
||||||||||||||
т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(C − A)sin2α +2Bcos2α =0, |
|
|
|
|
|
|
|
|
(7.46) |
|||||||||
т.е. 2Bcos2α =(A−C)sin2α.. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отсюда |
|
|
2B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg2α = |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(7.47) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
A−C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, при повороте осей на угол α, удовлетворяющий условию |
||||||||||||||||||
(7.47), уравнение (7.46) сводится к уравнению |
|
|
|
|
|
|
|
|
|
|||||||||
Ax2 + Cy2 + 2Dx + 2Ey + F = 0 . |
|
|
|
|
|
|
|
|
(7.48) |
|||||||||
Вывод: общее уравнение второго порядка (7.45) определяет на плоскости следующие кривые: окружность, гиперболу, эллипс, параболу.
7.7 Вопросы для самоконтроля
1 |
Сформулируйте определение аффинной системы координат на |
|
плоскости. |
|
|
2 |
Сформулируйте определение координат точки |
относительно |
аффинного репера. |
|
|
3 |
Как найти координаты вектора по координатам точек его начала и |
|
конца? |
|
|
4Запишите формулы для нахождения координат точки, делящей отрезок
вотношении λ.
5Сформулируйте определение прямоугольной декартовой системы координат на плоскости.
188