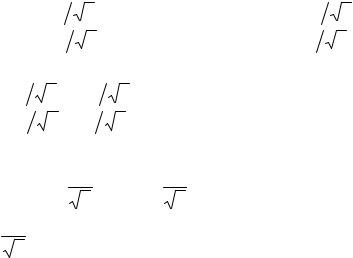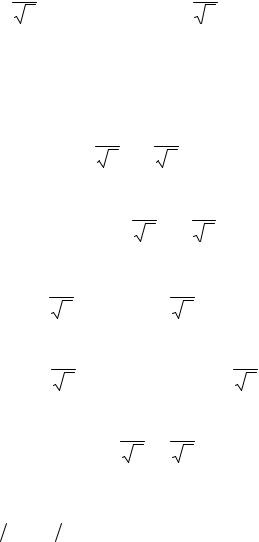Квадратичная форма f (x1, x2 , ..., xn ) с действительной матрицей
является положительно определенной тогда и только тогда, когда все ее главные миноры положительны.
Например: 1) Квадратичная форма
f = 5x12 + x22 + 5x32 + 4x1x2 −8x1x3 − 4x2 x3
положительно определена, так как ее главные миноры
5, |
|
5 |
2 |
|
=1, |
|
5 |
2 |
− 4 |
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
− 2 |
|
=1 |
|
|
2 |
1 |
|
|
|
− 4 |
− 2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
положительны.
2) Квадратичная форма
f = 3x12 + x22 + 5x32 + 4x1x2 −8x1x3 − 4x2 x3
не будет положительно определенной, так как ее второй главный минор отрицателен:
3 2 = −1.
2 1
Заметим, что по аналогии с положительно определенными квадратичными формами можно ввести отрицательно определенные формы, т.е. такие невырожденные квадратичные формы с действительными коэффициентами, нормальный вид которых содержит лишь отрицательные квадраты неизвестных.
Вырожденные квадратичные формы, нормальный вид которых состоит из квадратов одного знака, называются иногда полуопределенными. Наконец, неопределенными будут такие квадратичные формы, нормальный вид которых содержит как положительные, так и отрицательные квадраты неизвестных.
Приведем также без доказательства теорему о необходимом и достаточном условии того, что квадратичная форма является отрицательно определенной.
Теорема 12.7 Квадратичная форма является отрицательно определенной тогда и только тогда, когда ее главные миноры четного порядка положительны, а нечетного – отрицательны.
12.6 Приведение квадратичной формы к каноническому виду
Докажем, что действительную квадратичную форму можно привести к каноническому виду с помощью ортогонального оператора.
Теорема 12.8 Если существует ортогональный оператор с матрицей С, |
приводящий |
действительную |
|
квадратичную форму |
f = f (x1, x2 , ..., xn ) |
к |
каноническому виду |
|
|
|
|
|
|
|
|
ϕ(y , y |
2 |
, ..., y |
n |
)= λ y2 + λ |
2 |
y2 + ... + λ |
n |
y2 , |
(12.27) |
1 |
|
|
1 1 |
2 |
n |
A квадратичной формы |
то λ1, λ2 , ..., λn |
- характеристические числа матрицы |
f , причем столбцами матрицы С являются собственные векторы-столбцы
матрицы A с собственными числами λ1, λ2 , ..., λn . |
|
X = CY , где |
C = (cij ), |
Доказательство. Пусть |
ортогональный оператор |
приводит квадратичную форму |
f к каноническому виду (12.27), тогда матрица |
квадратичной формы ϕ имеет вид |
|
|
|
|
|
|
λ1 |
0 ... |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = |
0 |
λ2 ... |
0 |
|
. |
|
|
|
|
|
|
|
(12.28) |
... ... ... |
... |
|
|
|
|
|
|
|
|
|
|
0 |
0 ... |
λn |
|
|
|
|
|
|
|
|
|
|
Поскольку |
D = CT AC |
и C - ортогональная матрица, то |
СT = С−1 ; |
следовательно, D = C −1 AC , откуда получаем, что λi |
- характеристические числа |
матрицы A. |
|
|
|
|
|
|
|
|
|
|
|
|
D = CT AC, CCT = E и умножая обе |
Принимая во внимание выражения |
части равенства (12.28) на C слева, получаем (так как CD = CC −1 AC = AC ) |
|
|
|
|
|
λ1 |
|
0 |
... |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AC = С |
0 |
λ2 |
... |
0 |
|
|
. |
|
|
|
(12.29) |
... ... |
... |
... |
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
... |
λn |
|
|
|
|
|
|
|
Для |
|
|
элементов |
bij |
(i |
=1, 2, ..., n) |
матрицы |
B = AC согласно |
правилу |
умножения матриц имеем |
bij = ai1c1 j + ai2c2 j +... + aincnj . |
С другой стороны, из |
равенства (12.29) следует, что bij = cij λj , поэтому |
|
|
|
ai1c1 j |
+ ai2c2 j +... + aincnj |
= λj cij (i =1, 2, ..., n), |
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
1 j |
|
|
1 j |
|
|
|
|
|
|
|
|
|
c2 j |
|
c2 j |
|
|
|
|
|
|
|
|
|
A M |
|
= λj |
M |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
c |
nj |
|
|
|
|
|
|
|
|
|
|
nj |
|
|
|
|
(j =1, 2, ..., n) |
|
|
|
|
Итак, |
|
j -й |
столбец |
матрицы |
C |
является собственным |
вектором-столбцом матрицы A с собственным числом λj .
Теорема 12.9 Для любой действительной квадратичной формы существует ортогональный оператор, приводящий ее к каноническому виду.
Теорема 12.10 Для любой действительной симметрической матрицы A
существует такая ортогональная матрица T , что T −1 AT - диагональная матрица.
Доказательство. Пусть A - действительная симметрическая матрица порядка n , f (x1, x2 , ..., xn ) - квадратичная форма с матрицей A. По предыдущей
теореме существует ортогональное преобразование, приводящее эту форму к каноническому виду. Матрицу этого преобразования обозначим через Т , тогда
T T AT = D , где D - диагональная матрица. Поскольку Т - ортогональная матрица,
т.е. T T =T −1 , то T −1 AT = D - диагональная матрица.
Следствие Любая действительная симметрическая матрица может быть приведена к диагональному виду.
Теорема 12.11 Если линейный оператор действительного линейного пространства имеет действительную симметрическую матрицу в некотором ортонормированном базисе, то существует ортонормированный базис, состоящий из собственных векторов этого оператора.
Доказательство. Пусть A - действительная симметрическая матрица линейного преобразования f в ортонормированном базисе e1, e2 , ..., en , Согласно
теореме 12.10 существует такая ортонормированная матрица Т , что T −1 AT - диагональная матрица. Как известно, ортогональное преобразование Т переводит ортонормированный базис e1, e2 , ..., en в ортонормированный базис e1′, e2′ , ..., en′ , в
котором матрица f является диагональной. Это означает, что e1′, e2′ , ..., en′ - собственные векторы оператора f .
Из доказанных теорем получаем алгоритм нахождения ортогонального преобразования, приводящего квадратичную форму n переменных к каноническому виду:
1)записываем матрицу данной квадратичной формы, находим ее собственные значения и n попарно ортогональных собственных векторов, нормируем их;
2)составляем матрицу из ортонормированных собственных векторов-
столбцов;
3)записываем искомый ортогональный оператор с помощью последней
матрицы.
Критерий Сильвестра
Квадратичные формы подразделяют на различные типы в зависимости от множества их значений.
Квадратичную форму f(x) = xT Ax , x = (x1 ... xn )T , будем называть:
- положительно (отрицательно) определенной, если для любого ненулевого столбца x выполняется неравенство f ( x ) > 0 ( f ( x ) < 0 );
301

- неотрицательно (неположительно) определенной, если f ( x ) ≥ 0 ( f ( x ) ≤ 0 ) для любого столбца x , для которого f ( x ) = 0 ;
-знакопеременной (неопределенной), если существуют такие столбцы x
иy , что f ( x ) > 0 и f ( y ) < 0 .
Как следует из определения, тип квадратичной формы зависит только от множества значений, которые она принимает, но не зависит от переменных, в которых она записана. Поэтому, представив квадратичную форму в каноническом виде, получаем следующие критерии для типа квадратичной формы в зависимости от множества собственных значений ее матрицы.
|
Тип |
квадратичной |
Множество собственных значений |
|
формы |
|
|
|
|
|
|
|
|
|
Положительно |
Все |
собственные |
значения |
|
определенная |
|
положительны (λi > 0, i = |
|
|
) |
|
|
|
1, n |
|
|
( x ≠ 0 : f ( x ) > 0) |
Все |
собственные |
значения |
|
Отрицательно |
отрицательны (λi < 0, i = |
|
) |
|
|
1, n |
|
|
определенная |
|
Есть |
собственные значения |
разных |
|
( x ≠ 0 : f ( x < 0 )) |
|
знаков ( λi |
> 0, λj > 0) |
|
|
Знакопеременная |
Есть |
нулевое собственное |
значение |
|
( x : f ( x ) > 0, y : f ( y ) < 0) |
|
( λ = 0). |
|
|
|
|
|
|
|
Вырожденная |
i |
|
|
|
|
|
|
|
( x : x ≠ 0, f ( x ) = 0), |
|
|
|
|
|
|
|
Хотя эта таблица дает удобную характеристику типам квадратичных форм, ее использование для определения типа конкретной квадратичной формы связано с вычислением собственных значений матрицы. А это достаточно трудоемкая операция. На самом деле во многих случаях тип квадратичной формы можно определить, не вычисляя собственных значений ее матрицы. Метод состоит в вычислении и проверке знаков некоторых миноров матрицы квадратичной формы. Введем следующие обозначения.
Пусть матрица квадратичной формы f ( x ) = xT Ax имеет вид
a |
a |
... |
a |
|
|
11 |
12 |
|
1n |
|
a21 |
a22 |
... |
a2n |
, |
A = |
... |
... |
... |
|
... |
|
|
|
an2 |
... |
|
|
|
an1 |
ann |
|
где aij = a ji , i, j =1, n . Рассмотрим угловые миноры этой матрицы (которые также называют главными минорами):
|
|
|
|
|
|
a11 |
a12 |
|
|
|
a11 |
... |
an |
|
|
|
|
|
|
|
|
|
∆ |
1 |
= a , |
∆ |
2 |
= |
, …, ∆ |
n |
= |
... ... ... |
. |
|
11 |
|
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1 |
... |
ann |
|
|
|
|
|
|
|
|
|
|
|
|
|

Как видим, угловой минор порядка k расположен на пересечении первых k строк и первых k столбцов матрицы. Угловой минор максимального, n -го порядка представляет собой определитель матрицы.
Теорема 12.12 (критерий Сильвестра) Для того чтобы квадратичная форма от n переменных была положительно определена, необходимо и достаточно, чтобы выполнялись неравенства ∆1 > 0 , ∆2 > 0 , ∆3 > 0 , …, ∆n > 0 .
Следствие 1 Для того чтобы квадратичная форма n переменных была отрицательно определена, необходимо и достаточно, чтобы выполнялись
неравенства − ∆1 > 0 , ∆2 > 0 , − ∆3 > 0 , …, ( −1)n ∆n > 0 (знаки угловых миноров
чередуются начиная с минуса).
Доказательство. Если квадратичная форма f ( x ) отрицательно определена, то квадратичная форма − f ( x ) положительно определена, и наоборот. Матрицей квадратичной формы − f ( x ) является матрица − A , противоположная матрице A квадратичной формы f ( x ). Согласной критерию Сильвестра, для положительной определенности квадратичной формы − f ( x ) необходимо и достаточно, чтобы все угловые миноры ∆′r , r =1, n , матрицы − A были положительны. Но при умножении матрицы A на число −1 все ее элементы умножаются на это число и поэтому ∆′r =( −1)r ∆r , где ∆r - угловой минор порядка r матрицы A. Таким образом, квадратичная форма − f ( x ) положительно определена тогда и только тогда, когда выполнены неравенства ( −1)r ∆r > 0 , r =1, n , и это условие эквивалентно тому, что квадратичная форма f ( x ) отрицательно определена.
Следствие 2 Невырожденная квадратичная форма знакопеременна тогда и только тогда, когда для матрицы квадратичной формы выполнено хотя бы одно из условий:
-один из угловых миноров равен нулю;
-один из угловых миноров четного порядка отрицателен;
-два угловых минора нечетного порядка имеют разные знаки.
Доказательство. Невырожденная квадратичная форма может либо
положительно определенной, либо отрицательно определенной, либо знакопеременной – в зависимости от знаков коэффициентов в ее каноническом виде. Если имеется нулевой угловой минор или один из угловых миноров четного порядка отрицателен, то, согласно теореме 12.12 и следствию 1, эта квадратичная форма не является ни положительно, ни отрицательно определенной. То же можно утверждать и в случае, когда есть два угловых минора нечетного порядка с разными знаками. Значит, в этих случаях квадратичная форма знакопеременная.
Критерий Сильвестра и его следствия показывают, что тип квадратичной формы полностью определяется свойствами ее матрицы. Поэтому термины, введенные определением, можно перенести на симметрические матрицы. В частности, симметрическую матрицу A называют положительно
(отрицательно) определенной и пишут A > 0 ( A < 0 ), если положительно
(отрицательно) определена соответствующая квадратичная форма. Согласно теореме 12.12 и ее следствиям, симметрическая матрица положительно определена, если все ее угловые миноры положительны. Симметрическая матрица отрицательно определена, если у ее угловых миноров знаки чередуются начиная со знака минус.
Следствие 3 Если симметрическая матрица положительно определена, то все ее диагональные элементы положительны.
Доказательство. Если A = (aij ) - симметрическая положительно
определенная матрица порядка n , то ее первый угловой минор положителен, т.е. a11 = ∆1 > 0 . Воспользовавшись тем, что утверждение следствия верно для
диагонального элемента a11 , докажем что и aii > 0 при i > 0 . В квадратичной форме xT Ax , x = (x1 , ..., xn )T сделаем замену переменных
x1 = yi , |
xi = y1 , |
x j = y j при j ≠1, i . |
В новых переменных матрица A′ = (aij′ ) квадратичной формы такова, что
aii = a11′ > 0 .
Рассмотрим примеры на применение критерия Сильвестра. 1) Квадратичная форма xT Ax от трех переменных с матрицей
|
1 |
0 |
−1 |
|
0 |
1 |
1 |
|
A = |
|
|
−1 |
1 |
3 |
|
|
|
Положительно определена, так как ∆1 = ∆2 = ∆3 =1 > 0 . |
2) Квадратичная форма xT Ax от трех переменных с матрицей
|
1 |
− 3 |
1 |
|
|
− 3 |
1 |
|
|
A = |
−1 |
|
1 |
−1 |
5 |
|
|
|
является знакопеременной, так как она невырождена ( ∆3 ≠ 0 ) и ∆1 =1 > 0 , а
∆2 = −8 < 0 .
3)Квадратичная форма 2x1x2 от двух переменных является знакопеременной, так как она невырождена ( ∆2 = −1 ≠ 0 ), а ∆1 = 0 .
4)Квадратичная форма f (x1 , x2 , x3 , x4 )= 4x1x3 + 2x2 x4 + x42 имеет угловые
миноры ∆1 = ∆2 = ∆3 = 0 , ∆4 = 4 и, согласно следствию 2, является
знакопеременной. В этом можно убедиться, используя несложное преобразование вида квадратичной формы:
f (x1 , x2 , x3 , x4 )= (x1 + x3 )2 − x22 − (x1 − x3 )2 + (x2 + x4 )2 .
12.7 Применение теории квадратичных форм в задачах о приведении к каноническому виду уравнения кривой второго порядка и уравнения поверхности второго порядка
1 Приведение уравнения кривой второго порядка к каноническому виду
Дано уравнение кривой второго порядка в прямоугольной системе координат Oxy
a |
x2 + 2a |
xy + a |
22 |
y2 + 2b x + 2b y + c = 0 . |
(12.30) |
11 |
12 |
|
1 |
2 |
|
Требуется с помощью поворота и параллельного переноса осей координат перейти к такой прямоугольной системе координат, в которой уравнение кривой имеет канонический вид.
Рассмотрим квадратичную форму, связанную с уравнением (12.30),
a11x2 + 2a12 xy + a22 y2 .
Ее матрица имеет вид
A = |
a |
a |
|
|
|
|
|
11 |
12 |
. |
|
|
|
|
|
a |
a |
22 |
|
|
|
|
|
|
|
12 |
|
|
|
|
λ1(x′)2 + λ1(y′)2 |
Приведем |
квадратичную форму |
к каноническому |
виду |
ортогональным оператором |
|
|
|
x |
|
x′ |
|
|
|
(12.31) |
|
|
= P |
. |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
y′ |
|
|
|
A, а столбцами |
Напомним, что λ1, λ2 - собственные значения матрицы |
матрицы |
|
P |
являются ортогональные |
нормированные |
собственные векторы |
(столбцы) матрицы A. Их всегда можно выбрать так, что det P =1. Матрица P в силу свойства ортогональных матриц второго порядка имеет вид
cosϕ |
− sinϕ |
, |
P = |
|
sinϕ |
cosϕ |
|
т.е. P - матрица оператора поворота на угол ϕ в пространстве V2 векторов на плоскости. При таком повороте прямоугольная система координат Oxy с координатными векторами i, j (базис в пространстве V2 ) переходит в прямоугольную систему координат Ox′y′ с координатными векторами i′, j′ (другой базис в пространстве V2 ), причем (i′ j′)= (i j)P .
Пользуясь формулами (12.31), выразим, линейные члены 2b1x + 2b2 x уравнения (12.30) через координаты x′, y′. В результате в системе Ox′y′ уравнение кривой примет вид
λ1(x′)2 + λ1(y′)2 + 2b1′x′ + 2b2′ y′ + c = 0 ,
т.е. в уравнении отсутствует смешанный член (с произведением x′y′).
Далее, выделив полные квадраты по обеим переменным (или по одной переменной, если одно из чисел λi равно нулю), с помощью параллельного
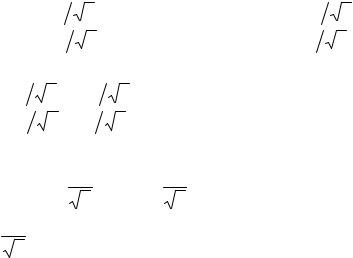
переноса осей координат системы Ox′y′ переходим к системе O′x′′y′′, в которой
уравнение кривой имеет канонический вид.
Напомним известные вам сведения из аналитической геометрии. Уравнение кривой второго порядка может быть приведено к одному из следующих канонических видов:
|
x2 |
+ |
|
y2 |
=1 |
или |
x2 |
+ |
|
y2 |
= −1 |
или |
x2 |
+ |
|
y2 |
= 0 , |
если |
кривая |
|
a2 |
|
b2 |
a2 |
|
b2 |
a2 |
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
эллиптического типа; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
− |
|
y2 |
=1 |
или |
x2 |
− |
|
y2 |
= −1 |
или |
x2 |
− |
|
y2 |
= 0 , |
если |
кривая |
|
a2 |
|
b2 |
a2 |
|
b2 |
a2 |
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гиперболического типа; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 = 2 py или |
y2 = 2 px (p ≠ 0) или |
y2 = a |
или |
x2 = a , |
если |
кривая |
параболического типа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, приведем уравнение кривой второго порядка |
|
|
11x2 − 20xy − 4 y2 − 20x − 8y +1 = 0 |
|
|
|
|
|
|
|
(12.32) |
к каноническому виду с помощью поворота осей координат системы Oxy и последующего параллельного переноса.
Решение. Приведем квадратичную форму 11x2 − 20xy − 4 y2 , связанную с
уравнением (12.32), ортогональным оператором к каноническому виду. С этой целью составим матрицу квадратичной формы:
|
|
|
11 |
|
−10 |
|
, |
|
|
|
|
|
|
|
|
|
A = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−10 |
|
− 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и запишем характеристическое уравнение: |
|
|
|
|
|
11 − λ |
|
−10 |
|
= λ2 − 7λ −144 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
−10 |
− 4 − λ |
|
|
|
|
Оно имеет корни λ1 = −9 , |
λ2 =16 . Далее находим взаимно ортогональные |
нормированные |
собственные векторы (столбцы) |
F1 и F2 матрицы A: если |
λ = −9 , то F |
|
1 |
5 |
|
; если λ |
|
=16 , то F |
|
− 2 |
5 |
|
= |
|
|
|
2 |
= |
|
|
. |
1 |
|
1 |
|
2 |
5 |
|
|
|
|
2 |
|
1 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, искомое ортогональное преобразование имеет матрицу |
|
|
1 |
5 |
|
− 2 |
5 |
|
|
|
|
|
|
|
|
|
P = |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
2 |
5 |
1 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у которой det P =1. Матрица P является матрицей оператора поворота на угол ϕ
такой, что cosϕ = |
1 |
, sinϕ = |
2 |
. Повернув оси координат системы Oxy на угол |
|
1 |
|
5 |
|
5 |
|
|
|
ϕ = arccos |
(против часовой стрелки), получим прямоугольную систему |
′ ′ |
. |
5 |
Ox y |
При этом координаты точек преобразуются по формуле
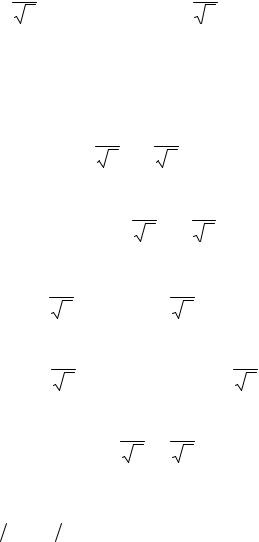
x |
= |
x′ |
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
y |
|
y′ |
|
|
или |
|
15 (x′ − 2 y′), |
y = 15 (2x′ + y′). |
|
x = |
(12.33) |
При ортогональном преобразовании (12.33) квадратичная форма переходит в форму
λ1(x′)2 + λ1(y′)2 = −9(x′)2 +16(y′)2 .
Запишем в новых координатах линейные члены уравнения (12.32):
−20x −8y = − 365 x′ + 325 y′.
Всистеме координат Ox′y′ уравнение кривой принимает вид
−9(x′)2 +16(y′)2 − 365 x′ + 325 y′ +1 = 0 .
Выделяя полные квадраты по обеим переменным, получаем
|
|
|
|
+ |
2 |
2 |
|
1 |
2 |
+ 5 = 0 . |
− 9 x′ |
5 |
|
+16 y′ + |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагая |
2 |
|
|
|
|
|
|
|
1 |
|
x |
′′ |
= x |
′ |
+ |
, |
y |
′′ |
= y |
′ |
+ |
, |
|
|
5 |
|
|
5 |
т.е. производя параллельный перенос осей координат так, что начало координат
|
|
|
|
− |
2 |
, − |
1 |
|
переходит в точку O′ |
5 |
5 |
приходим к каноническому уравнению данной |
кривой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x′′)2 |
− |
(y′′)2 |
=1. |
|
|
|
|
5 9 |
|
5 16 |
|
|
|
|
|
|
Это – каноническое уравнение гиперболы в системе координат O′x′′y′′.
2 Приведение уравнения поверхностей второго порядка к каноническому виду
Фигурой второго порядка в пространстве называется множество точек пространства, декартовы координаты которых удовлетворяют уравнению
a x2 |
+ a |
22 |
y2 + a |
33 |
z2 + |
2a xy + 2a xz + 2a |
23 |
yz + a x + |
11 |
|
|
|
12 |
13 |
14 |
+ a24 y + a34 z + a44 |
= 0 , |
|
|
|
(12.34) |
где a112 + a222 + a332 + 2 a122 + 2 a213 a232 ≠ 0 .
Сумма первых шести членов левой части уравнения (12.34) представляет собой квадратичную форму трех переменных x, y, z :
f (x, y, z) = a |
|
x2 + a |
22 |
y2 |
+ a |
33 |
z2 |
+ 2a |
|
xy + 2a xz |
+ 2a |
23 |
yz |
(12.35) |
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
13 |
|
|
|
|
с симметрической матрицей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
12 |
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
a12 |
a22 |
|
|
a23 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12.36) |
|
|
|
a |
a |
23 |
|
|
a |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
центральной, |
если det A ≠ 0 , и |
Фигура |
второго |
порядка |
|
называется |
|
нецентральной, если det A = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С помощью ортогонального преобразования квадратичная форма (12.35) |
приводится к каноническому виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ(x′, y′, z′) |
= λ1 x′2 + λ2 y′2 + λ3 z′2 , |
|
|
|
|
|
|
|
уравнения det(A − λE)= 0 . |
где |
|
λ1 , λ2 , λ3 |
|
- |
|
корни |
характеристического |
Матрица квадратичной формы ϕ =ϕ(x |
′ |
|
′ |
′ |
) имеет вид |
|
|
|
|
, |
y , z |
|
|
|
|
|
|
|
|
λ |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C = |
|
1 |
λ2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12.37) |
|
0 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Указанный ортогональный оператор уравнение (12.34) приводит к |
уравнению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ1x |
′2 |
+ λ2 y |
′2 |
+λ3 z |
′2 |
|
|
′ |
|
′ |
|
|
′ |
|
′ |
|
′ |
|
′ |
′ |
|
|
|
|
(12.38) |
|
|
|
|
|
|
+ a14 x |
|
+ a24 y |
|
+ a34 z |
|
+ a44 = 0 . |
|
|
|
Например, перейдем к такой прямоугольной системе координат, в которой |
уравнение поверхности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3y2 + 3z2 + 4xy + 4xz − 2 yz −12 |
30x −14 |
30 y + 2 30z + 506 = 0 |
(12.39) |
имеет канонический вид, и определим тип поверхности. |
|
|
|
|
Решение. Квадратичная форма |
|
|
|
|
|
|
|
|
|
|
|
|
|
3y2 + 3z2 + 4xy + 4xz − 2 yz , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
связанная с уравнением (12.39), имеет матрицу |
|
|
|
|
|
|
|
0 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
этой матрицы есть λ1 = −2 , |
|
λ2,3 = 4 , |
а столбцы |
Собственные |
|
значения |
|
(векторы) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 6 |
|
|
|
|
|
|
|
|
1 5 |
|
|
|
|
|
|
|
|
2 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, F |
= |
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
F = 1 6 |
2 5 |
, |
|
|
|
= −1 30 |
|
|
|
|
|
1 |
|
|
1 6 |
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
3 |
|
|
|
5 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
являются попарно ортогональными нормированными ее собственными векторами. Определитель матрицы, составленной из этих столбцов, равен −1,