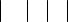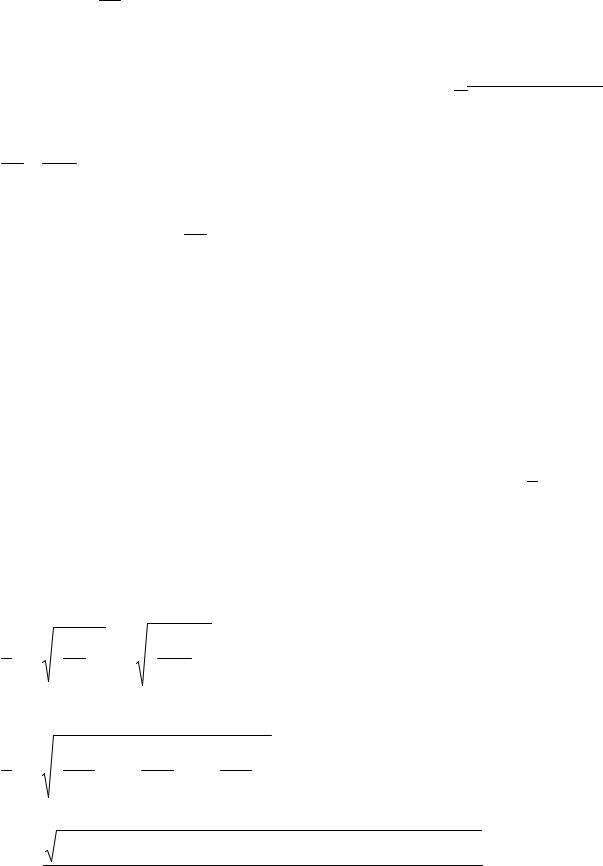Рисунок 108
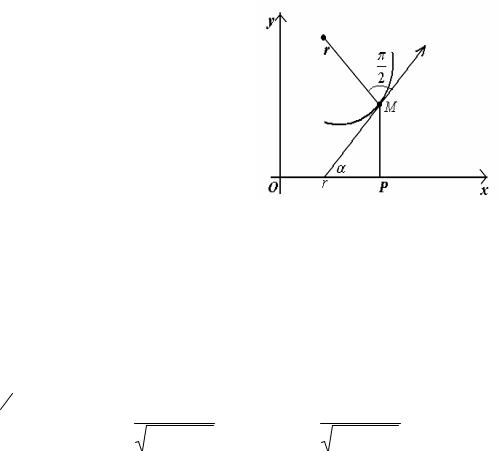
Рассмотрим теперь произвольную кривую и пусть ее касательная в какойлибо точке M образует с осью абсцисс угол α , тогда касательная в точке M ′, близкой к первой, будет наклонена к оси Ox под углом α + ∆α . Угол (α + ∆α)−α = ∆α будет углом поворота от первой касательной до второй, т.е. углом смежности двух близких касательных (рисунок 108. Так как α можно считать функцией длины дуги s (непосредственно или через посредство того параметра, функциями которого определяются координаты точек кривой), следовательно, кривизна в точке M выразится формулой
|
K = lim |
∆α |
или |
K = dα . |
|
|
∆s→0 |
∆s |
|
ds |
|
|
Так как угол α (а, следовательно, и dα ) измеряется отвлеченным числом, |
|
а дуга s (и ds ) |
зависит от выбранной линейной единицы масштаба, то |
|
подразмерность кривизны кривой K будет равной −1 относительно линейной |
|
единицы. Таким образом, |
размерность ее обратной величины |
1 |
будет равной |
|
K |
|
|
|
|
|
|
единице. Это замечание означает, что число K1 при изменении линейной единицы масштаба будет изменяться так же, как будут изменяться и все другие числа,
измеряющие те или иные отрезки. Вот почему число K1 мы имеем право считать
за число, измеряющее некоторый отрезок. Назовем число K1 радиусом кривизны
кривой в данной точке и обозначим через r : r = K1 ,
или
K = 1r .
Согласно определению, кривизна (так же, как и радиус кривизны) может быть и положительной, и отрицательной в зависимости от знака dα или ∆α при положительном ds и ∆s . Если ∆α положительно, то касательная в точке M ′ от касательной в точке M повернута в положительном направлении. Следовательно, вогнутость кривой находится в сторону положительного направления нормали (т.к. нормаль получается поворотом касательной в положительном направлении
|
|
π |
|
M |
′ |
от касательной |
|
на угол |
2 ). Если же ∆α |
отрицательно, то касательная в точке |
|
|
|
в точке |
M повернута |
в отрицательном направлении, т.е. |
вогнутость кривой |
обращена в сторону отрицательного направления нормали. Обратно, если r положительно, то dα и ∆α положительны, а потому вогнутость кривой обращена в сторону отрицательного направления нормали.
Поскольку радиус кривизны является отрезком, мы можем условиться откладывать его по нормали от точки кривой. При этом, если r положителен, то мы его будем откладывать от точки кривой по положительному направлению нормали. Конец радиуса кривизны, отложенного по нормали от точки кривой, назовем центром кривизны в данной точке кривой.
Пусть кривая теперь задана параметрическими уравнениями |
x = x(t), |
y = y(t). |
Найдем выражение кривизны в декартовых координатах.
Так как угол касательной с осью абсцисс в этом случае равен
α = arctg xy′′ ,
то
dα = x′y′′ − x′′y′dt ; x′2 + y′2
причем
ds = x′2 + y′2 dt .
Следовательно, кривизна кривой определяется соотношением
|
dα |
|
′ ′′ |
′′ ′ |
|
K = |
= |
x y |
− x y |
, |
ds |
(x′2 + y′2 )32 |
а радиус кривизны соотношением
r= (x′2 + y′2 )32 .
x′y′′− x′′y′
Если кривая дана уравнением y = f (x) ,
то ее кривизна и радиус кривизны определяется формулами:
|
y |
′′ |
|
|
|
|
′2 |
32 |
K = |
|
|
, |
r = |
(1 + y |
|
) . |
|
3 |
2 |
y |
′′ |
|
(1 + y′2 ) |
|
|
|
|
Найденные выражения показывают, что радиус кривизны кривой в какойлибо ее точке есть радиус окружности, соприкасающейся с кривой в данной ее точке. Центр кривизны в данной ее точке будет центром соответствующей этой точке соприкасающейся окружности. Кривизна кривой обращается в нуль, а радиус кривизны – в бесконечность в точках перегиба, т.е. в таких точках, в которых касательная прямая имеет с кривой соприкосновение 2-го порядка, или, иначе, соприкасающаяся окружность обращается в прямую линию.
Первоначальное определение кривизны кривой, очевидно, не зависит ни от какой системы координат, поэтому указанное выше выражение радиуса кривизны через декартовы координаты и их производные сохраняется при переходе к любой другой (прямоугольной же) декартовой системе координат. Таким образом,
кривизна кривой или радиус кривизны являются инвариантами по отношению к любому преобразованию координат (декартовой к декартову).
Кривизна кривой и ее радиус кривизны кривой, вообще говоря, меняются от одной точки к другой. Следовательно, радиус кривизны является функцией длины дуги, отсчитываемой от некоторой определенной точки кривой. Очевидно, что если выражение радиуса кривизны дано в зависимости от длины дуги, то можно вполне определить вид кривой, не считаясь с ее положением на плоскости.
По этой причине каждое из уравнений |
f (r, s)= 0 |
или |
r = f (s) |
называют натуральным уравнением кривой.
По выражению радиуса кривизны в функции дуги s легко определить точки перегиба или точки заострения кривой (точки возврата); в самом в первом случае радиус кривизны становится бесконечным, во втором случае он обращается в нуль.
13.4 Эволюта. Эвольвенты
Эволютой, или разверткой, для данной кривой назовем геометрическое место центров ее кривизны. Поскольку центр кривизны является центром соприкасающейся окружности, то эволюта будет
одновременно |
и |
|
|
местом |
центров |
|
соприкасающихся окружностей данной кривой. |
|
|
Координаты |
центра |
кривизны |
кривой |
|
можно |
получить, если к координатам точки M |
|
кривой прибавить соответственно проекции на |
|
оси координат радиуса кривизны, отложенного от |
|
точки |
M по нормали кривой. Пусть α |
- угол |
|
касательной в точке M с осью Ox (рисунок 109), |
|
тогда угол нормали с той же осью будет α + π . |
|
|
|
|
|
|
|
2 |
|
Таким образом, координаты центра кривизны выражаются |
Рисунок 109 |
Следующим образом: |
π |
|
|
|
|
|
α + |
η = y + r cosα , |
|
|
ξ = x + r cos |
2 |
, |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
ξ = x − r sinα, |
|
η = y + r cosα . |
|
|
|
|
(13.14) |
Принимая во внимание выражения |
|
|
|
|
|
|
|
r = |
(x′2 + y′2 )32 |
, |
cosα = |
|
x′ |
, |
sinα = |
|
y′ |
, |
|
′ ′′ |
′′ ′ |
|
x′ |
|
+ y′ |
|
x′ |
|
+ y′ |
|
|
x y |
− x y |
|
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
окончательно находим:
|
|
x′2 + y′2 |
|
|
ξ = x − |
|
|
|
|
y′, |
|
′ ′′ |
|
′′ ′ |
|
|
x y |
|
− x y |
|
|
|
|
x′2 + y′2 |
|
|
|
|
x |
′ |
η = y + |
|
|
|
|
|
|
|
′ |
′′ |
|
′′ ′ |
|
|
|
|
|
|
x y |
|
− x y |
|
|
или же для кривой, заданной уравнением y = f (x), |
|
1 + y′2 |
′ |
|
|
ξ = x − |
|
y′′ |
|
y , |
|
|
|
|
|
|
|
|
|
|
1 + y′2 |
′ |
|
|
|
|
|
η = y + |
|
|
|
|
x . |
|
|
|
y′′ |
|
|
|
|
|
|
|
|
Чтобы получить простейшие свойства эволюты, удобнее пользоваться ее уравнениями в виде (13.14); взяв дифференциалы от ξ и η , получаем:
dξ = dx − r cosα dα − sinα dr , |
dη = dy − r sinαdα + cosα dr ; |
но из соотношений |
|
|
|
|
|
dx = cosα , |
dx |
= sinα , |
dx |
= |
1 |
ds |
ds |
|
ds |
|
r |
следует, что |
|
|
|
|
|
dx = r cosα dα , |
|
dy = r sinα dα , |
|
|
потому |
|
|
|
|
|
dξ = −sinα dr , |
|
dη = cosα dr . |
|
(13.16) |
Составим отношение этих дифференциалов и сумму их квадратов:
|
dη |
= −ctgα , |
dξ2 + dη2 = dr2 ; |
(13.17) |
|
dξ |
|
|
|
|
первое соотношение показывает, что касательная к эволюте имеет направление нормали к кривой. Так как нормаль к кривой проходит через соответствующую точку эволюты, то, следовательно, касательной к эволюте и является сама нормаль к кривой. Иначе говоря, эволюта кривой есть огибающая ее нормалей.
Второе из соотношений (13.17) показывает, что дифференциал дуги эволюты по абсолютной величине равен абсолютному значению дифференциала радиуса кривизны кривой, т.е.
dσ = dr .
Допустим, что на участке кривой, где ее радиус кривизны возрастает, мы в том же направлении будем считать возрастающей и дугу эволюты, тогда
dσ = dr или σ2 −σ1 = r2 − r1 ,
т.е. приращение дуги эволюты равно приращению радиуса кривизны кривой.
Пусть точкам M1 и M 2 (рисунок 110) соответствуют радиусы кривизны
M1N1 = r1 , |
M 2 N2 = r2 , |
тогда дуга эволюты от точки N1 до точки N2 будет: |
|
|
N1N2 =σ2 |
−σ1 = M 2 N2 − M1N1. |
y = y(s);
Рисунок 110
Данная кривая относительно своей эволюты называется эвольвентой или развертывающей последней. На основании предыдущих предложений, если дана некоторая кривая, то ее эвольвенту, очевидно, можем получить следующим построением: на каждой касательной заданной кривой в обратную ее сторону следует откладывать дугу кривой, отсчитанную от некоторой ее произвольной выбранной точки. Нетрудно доказать и непосредственно, что это построение даст бесчисленное множество эвольвент данной линии, т.е. кривых, ортогональных в каждой своей точке к касательным начальной кривой. В самом деле, пусть кривая
изображается уравнениями x = x(s),
будем откладывать на каждой из ее касательных в обратную сторону отрезки, равные s + c , тогда геометрическое место концов этих касательных будет
|
|
|
= x − (s + c)x′, |
|
|
|
= y − (s + c)y′; |
(13.18) |
|
ξ |
η |
дифференцируя эти соотношения, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
dη = −(s + c)dy |
, |
|
dξ = −(s + c)dx |
, |
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
′ |
|
|
|
′ |
|
|
|
|
′ ′ |
|
′ ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
x dξ + y dη = −(s + c)(x dx |
+ y dy |
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
(13.19) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x dξ + y dη = 0 , |
|
|
|
|
|
|
|
|
так как
x′dx′ + y′dy′ = 0
в силу условия
x′2 + y′2 =1.
Соотношение (13.19) как раз и показывает нам, что касательная к кривой (13.18) при любом выборе постоянного с перпендикулярно к соответствующей касательной к данной кривой.
Взаимоотношение между данной кривой и ее эволютой на основании предыдущих свойств легко представить себе следующим наглядным способом: допустим, что на линию наложена гибкая нерастяжимая нить определенной
323
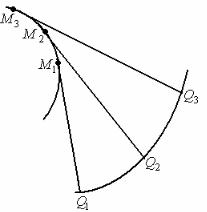
длины, закрепленная в какой-либо точке M 3 кривой (рисунок 111); если
сматывать нить, держа ее все время натянутой по направлению касательной в точке ее схода с кривой, то конец нити, занимая последовательно положения Q1,
Q2 , Q3 , … этой линии, и опишет развертывающую данной кривой.
Рисунок 111
Если дано натуральное уравнение кривой r = r(s),
то легко получить натуральное уравнение ее эволюты. В самом деле, будем соответствующими буквами со значком (′) обозначать элементы эволюты. В таком случае имеем:
|
|
′ |
|
|
π |
|
|
′ |
|
|
|
α |
=α + 2 |
, |
ds |
= dr , |
(13.20) |
|
|
|
|
r′ = |
ds′ |
|
dr |
dr |
|
|
|
|
= |
|
= r ds . |
(13.21) |
|
dα′ |
dα |
|
Таким образом, исключая из соотношений |
|
|
s′ = r(s) , |
|
|
|
r′ = r drds |
(13.22) |
параметр s (дугу начальной кривой), получим натуральное уравнение эволюты. Возьмем, например, натуральное уравнение циклоиды
r 2 + s2 =16a2 ; |
(α) |
дифференцируя его, получим |
|
rdr + sds = 0 , |
|
следовательно, |
|
r′ = −s ; |
(β) |
присоединяя сюда уравнение |
|
s′ = r |
(γ) |
и исключая r и s из уравнений (α), (β), (γ), найдем |
|
r′2 + s′2 =16a2 , |
|
т.е. эволютой циклоиды является та же циклоида (определенным образом расположенная относительно первой).
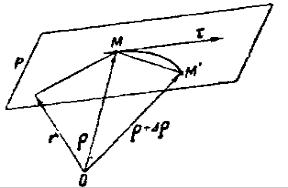
13.5 Соприкасающаяся плоскость |
|
|
|
|
Пусть τ будет вектор касательной к |
кривой |
в |
точке |
M (ρ). Возьмем |
плоскость, |
проходящую через касательную |
и еще |
через |
близкую точку |
′ |
кривой (рисунок 112). Обозначим через |
r |
вектор, |
определяющий |
M (ρ + ∆ρ) |
какую-либо точку указанной плоскости. Тогда три вектора r − ρ , τ , ∆ρ
будут компланарны, а потому их смешанное произведение обращается в нуль
(r − ρ)τ ∆ρ = 0 .
Рисунок 112
Когда точка M ′ неограниченно приближается к первой точке M , т.е.
когда ∆s стремится к нулю, |
левая часть предыдущего уравнения стремится к |
определенному пределу и само уравнение принимает вид |
′ |
′′ |
= 0 . |
(13.23) |
(r − ρ)ρ ρ |
|
Предельное положение плоскости, проходящей через касательную прямую и близкую точку кривой, называется соприкасающейся плоскостью кривой в заданной ее точке. Уравнение (13.23) является, таким образом, уравнением соприкасающейся плоскости кривой.
Соприкасающуюся плоскость можно было бы определить, как предельное положение плоскости, проходящей через три близкие точки кривой, когда две из них стремятся к совпадению с третьей.
Для плоской кривой соприкасающаяся плоскость будет одной и той же во всех точках кривой, именно, плоскостью самой кривой.
Если не делать предположения, что ρ есть функция дуги s , то уравнение (13.23) напишется в виде
|
|
|
|
|
|
(r − ρ) |
dρ |
|
dsd 2 ρ − dρ d 2 s |
= 0 |
|
|
|
ds |
ds2 |
|
или по упрощении |
|
|
(r − ρ)dρ d 2 ρ = 0 ; |
(13.24) |
отсюда следует, что уравнение (11.24) соприкасающейся плоскости сохраняет свой вид и в том случае, когда ρ есть функция любого параметра t .
В силу свойств тройного произведения векторов уравнения соприкасающейся плоскости в координатном изображении будет иметь вид
X − x |
Y − y |
Z − z |
|
|
|
|
|
x′ |
y′ |
z′ |
|
= 0 . |
(13.25) |
x′′ |
y′′ |
z′′ |
|
|
|
Например, составим уравнение соприкасающейся плоскости для кривой, заданной уравнениями
Решение. Приравнивая нулю полный дифференциал левой части каждого из данных уравнений, мы прежде всего найдем:
|
|
|
dx |
|
|
|
= |
|
|
|
|
dy |
|
|
|
= |
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
z |
|
|
|
z |
|
|
|
|
x |
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
с2 |
|
|
|
|
с2 |
|
|
a2 |
|
|
|
a2 |
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
z |
|
|
|
|
z |
|
|
|
|
x |
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
1 |
|
|
1 |
m |
|
|
|
|
|
|
|
1 |
|
|
1 m |
|
1 |
|
1 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
− |
|
|
|
|
|
|
, |
|
|
|
dy = |
|
|
|
|
|
− |
|
|
|
, |
dz = |
|
− |
|
|
|
, |
|
|
|
c2 |
x |
|
|
|
|
|
с2 |
a2 |
y |
|
b2 |
z |
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
где m - некоторый множитель пропорциональности. Отсюда далее получим:
|
2 |
|
1 |
|
|
1 |
|
|
mdx |
|
dm |
|
d |
|
x = |
|
|
|
− |
|
|
− |
|
|
+ |
|
, |
|
|
|
c2 |
x2 |
x |
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
mdy |
|
dm |
|
d 2 y = |
|
|
|
− |
|
|
|
|
− |
|
|
+ |
|
|
, |
|
2 |
|
|
2 |
|
|
2 |
|
|
|
c |
|
|
a |
|
|
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
1 |
|
|
|
mdz |
|
dm |
|
d |
|
z = |
|
|
|
|
− |
|
|
|
|
− |
z2 |
+ |
z |
; |
|
|
|
|
|
b |
|
|
|
|
a2 |
|
|
2 |
|
|
|
|
|
|
здесь коэффициенты |
|
при dm |
пропорциональны dx , dy , dz , поэтому при |
подстановке вторых дифференциалов в уравнение (13.25) члены с dm выпадают. Итак, уравнение искомой соприкасающейся плоскости может быть
написано в следующем виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X − x |
1 |
|
− |
1 |
|
1 |
|
1 |
|
− |
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
c2 |
|
|
|
|
b2 |
|
|
|
|
x |
|
b2 |
|
|
|
|
x3 |
|
|
Y − y |
1 |
|
− |
1 |
|
1 |
|
1 |
|
− |
1 |
|
2 |
1 |
|
= 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
a2 |
|
y3 |
|
c2 |
|
|
|
y |
|
c2 |
|
|
|
|
|
|
Z − z |
1 |
|
− |
1 |
|
1 |
|
1 |
|
− |
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
b2 |
|
|
|
|
|
a2 |
|
|
|
|
z |
|
a2 |
|
|
|
|
z3 |
|
|
развернув определитель левой части и использовав при этом для координат x , y , z точки касания уравнения самой линии, получим
|
r 2 − a2 |
|
x3 |
(X − x)+ |
r 2 − b2 |
|
y3 |
(Y − y)+ |
r 2 − c2 |
|
z3 |
(Z − z)= 0 . |
|
b2 − c2 a4 |
c2 − a2 b4 |
a2 − b2 c4 |
|
|
|
|
Показать, что соприкасающаяся плоскость остается неизменной для всех точек данной кривой, когда последняя распадается (например, при r 2 = b2 ).
13.6 Кривизна кривой
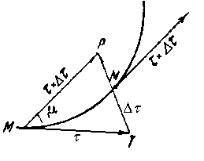
Пусть τ |
единичный вектор касательной к кривой |
в точке M , |
тогда τ + ∆τ |
- вектор касательной в точке M ′, близкой к первой. |
Перенесем |
параллельно |
вектор τ + ∆τ |
в точку M (рисунок 113). В этом случае вектор |
∆τ = |
TP |
по |
величине и направлению будет давать уклонение касательной при переходе от точки M к точке M ′. Отношение
∆τ ∆s
возьмем за |
меру |
кривизны кривой на протяжении |
|
|
|
|
|
дуги MM ′ = ∆s . Предел |
указанного отношения (когда ∆s стремится к нулю) |
|
|
|
|
|
dτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называется вектором кривизны кривой в точке M . |
|
|
|
|
Пусть P |
- конец вектора τ + ∆τ , параллельно перенесенного в точку M , и |
µ - угол (PMT ) |
двух близких касательных. Тогда |
|
|
|
|
|
∆τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
TP |
= |
TP |
|
TP |
= |
TP |
|
µ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆s |
|
|
|
∆s |
|
∆s |
∆s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TP |
|
|
|
TP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где TP - дуга окружности радиуса MT =1. Так как |
|
|
|
|
lim |
TP |
=1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то предыдущее соотношение при переходе к пределу |
|
|
даст величину вектора кривизны в виде |
|
|
|
Рисунок 113 |
|
dτ |
|
|
|
= |
|
lim |
|
µ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆s→0 ∆s |
|
|
|
|
|
|
|
|
|
|
|
|
Так как µ есть число, a |
∆s - длина дуги кривой, |
то, |
соблюдая размерность |
найденного отношения, можем положить |
|
|
|
|
|
dτ |
|
|
= |
|
lim |
|
µ |
|
= |
1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆s→0 ∆s |
|
|
r |
|
|
|
|
|
|
|
|
|
предполагая, |
|
что |
r |
|
есть некоторая длина. Величина |
|
1 |
|
называется кривизной |
|
|
|
r |
кривой в данной точке, а |
r |
|
|
|
|
|
называется радиусом кривизны кривой в данной |
точке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
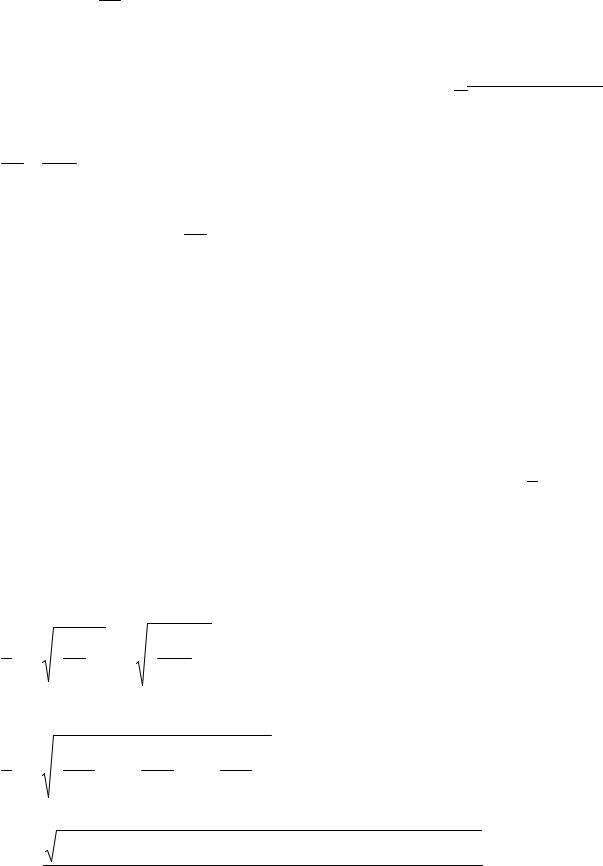
Отношение ∆µs можно называть средней скоростью поворота вектора τ на
единицу пройденной дуги ∆s кривой. Предел этого отношения называется скоростью вращения вектора τ . Доказанное выше предложение обозначает, что в каждой данной точке кривой скорость вращения вектора τ равна кривизне
кривой в данной точке.
Возвращаемся к вектору кривизны
dτ = d 2 ρ ; ds ds2
само построение показывает, что он направлен в сторону вогнутости кривой.
Далее, так как τ 2 =1 и τ ddsτ = 0, то вектор кривизны перпендикулярен к
касательной. Наконец, уравнение соприкасающейся плоскости
(r − ρ)ρ′ρ′′ = 0
удовлетворяет любой точкой r = ρ + uρ′′
вектора кривизны (считая, что он выходит из точки M кривой). Поэтому вектор кривизны лежит в соприкасающейся плоскости. Единичный вектор, перпендикулярный к касательной, лежащий в соприкасающейся плоскости и направленный в сторону вогнутости кривой (по вектору кривизны), будем называть главной нормалью кривой и обозначать буквой ν («ню» греческое).
Так как величину вектора кривизны мы обозначили через 1r , а его направление через ν , то
|
|
dτ |
= |
ν |
; |
|
|
|
|
|
(13.26) |
|
|
ds |
|
r |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
при этом согласно условию величина |
есть величина положительна и равна |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= + |
|
|
dτ |
2 |
d 2 |
ρ 2 |
|
(13.27) |
|
|
|
|
|
|
|
= + |
|
. |
|
|
|
r |
|
|
|
|
ds |
|
|
2 |
|
|
|
|
|
|
|
|
|
ds |
|
|
|
Это последнее соотношение легко дает радиус кривизны в координатном изображении
1 |
= + |
d 2 x 2 |
d 2 y 2 |
d 2 z |
2 |
|
|
|
+ |
|
|
+ |
|
(13.28) |
r |
|
|
2 |
|
ds |
2 |
|
2 |
|
|
ds |
|
|
|
ds |
|
|
или в более общем случае, когда x , y , z - функции любого параметра |
|
1 |
= + |
(dsd 2 x − dxd 2s)2 + |
(dsd 2 y − dyd 2 s)2 + (dsd 2 z − dzd 2s)2 |
. |
(13.29) |
|
r |
|
ds2 |
|
|
|
|
|
Из формулы (13.29) можно получить и другое выражение для кривизны. В самом деле, умножая обе части этого равенства векторно на τ , получим