Unlock-Линейная алгебра Сикорская 1

приводит квадратичную форму к следующему каноническому виду:

4(x′)2 − 2(y′)2 + 4(z′)2 .

С помощью формулы (12.40) вычислим в новых координатах линейные члены уравнения (12.39):

−12 30x −14 30 y + 2 30z = −40 6x′ +12 5y′.

Итак, в системе координат Ox′y′z′ с координатными векторами i′, j′, k′ уравнение поверхности имеет вид

4(x′)2 − 40 6x′ − 2(y′)2 +12 5y′ + 4(z′)2 + 506 = 0 .

Выделив полные квадраты по переменным x′ и y′, получим уравнение

4(x′ − 5 6 )2 − 2(y′ − 3 5)2 + 4(z′)2 − 4 = 0 .

Положим x′′ = x′ −5 6 , y′′ = y′ − 3 5 , z′′ = z′, т.е. произведем параллельный перенос осей координат системы Ox′y′z′ так, что начало координат перейдет в точку O′(5 6, 3 5, 0). В новой системе координат O′x′′y′′z′′ уравнение поверхности имеет канонический вид:

двуполостный гиперболоид

309

эллиптический параболоид

x2 + y2 = 2z ; a2 b2

гиперболический параболоид

x2 − y2 = 2z ; a2 b2

эллиптический цилиндр

гиперболический цилиндр

параболический цилиндр

x2 = 2z . a2

12.8 Вопросы для самоконтроля

1Сформулируйте определение квадратичной формы.

2Какая матрица называется матрицей квадратичной формы?

3Запишите квадратичную форму в матричном виде.

4Какой линейный оператор называется невырожденным?

5Какие две квадратичные формы называются конгруэнтными?

6Перечислите свойства конгруэнтности квадратичных форм.

7Сформулируйте и докажите теорему о преобразовании квадратичной

формы f линейным однородным оператором X = BY .

8Сформулируйте и докажите основную теорему о квадратичных

формах.

9Какой вид квадратичной формы называется нормальным?

10Сформулируйте и докажите теорему о приведении действительной квадратичной формы к нормальному виду.

11Сформулируйте и докажите теорему – закон инерции квадратичных

форм.

12Что значит положительный индекс инерции квадратичной формы (отрицательный индекс)?

13Дайте определение сигнатуры квадратичной формы.

310

14Сформулируйте и докажите теорему – необходимое и достаточное условия конгруэнтности двух действительных квадратичных форм.

15Что вы можете сказать об определителях матриц конгруэнтных невырожденных действительных квадратичных форм?

16Что значит знакоопределенные квадратичные формы?

17Сформулируйте и докажите условие существования положительно определенной квадратичной формы.

18Какие миноры называются главными минорами квадратичной формы f и как они влияют на знакоопределенность последней?

19Что значит отрицательно определенные, полуопределенные, неопределенные квадратичные формы?

20Сформулируйте и докажите теорему о приведении действительной квадратичной формы к каноническому виду с помощью ортогонального оператора.

21Сформулируйте и докажите теорему о существовании ортонормированного базиса, состоящего из собственных векторов оператора.

22Сформулируйте правило нахождения ортогонального оператора, приводящего квадратичную форму n переменных к каноническому виду.

23Как привести уравнение кривой второго порядка к каноническому

виду?

24Сформулируйте правило приведения уравнения поверхностей второго порядка к каноническому виду.

25Сформулируйте необходимое и достаточное условия существования отрицательно определенной квадратичной формы.

311

Глава 13 Геометрические объекты дифференциальной геометрии

13.1 Кривые. Способы задания кривых

Кривую на плоскости можно изобразить уравнением между текущими координатами ее точек.

Если кривая определяется по отношению к декартовой системе координат, то ее уравнение запишется в виде

или, предполагая данное уравнение разрешенным относительно ординаты y , в

Другим, достаточно удобным способом задания, кривой служит, так называемое, параметрическое изображение кривой, при котором каждая из двух ее текущих координат задается как функция некоторого параметра. Например, в

(13.1) можно получить разнообразными способами параметрическое изображение кривой. Действительно, если в уравнение (13.1) подставить вместо x произвольную функцию какого-либо параметра t , то оно определит y как

функцию1) того же параметра t , и получим уравнения кривой в форме (13.5). Параметр t , входящий в уравнение (13.5), может иметь иногда какое-либо

механическое или геометрическое значение, связанное со способом образования кривой.

Если, например, представить себе кривую как путь (траекторию), описываемый точкой, движущейся по какому-либо закону, то в каждый данный момент t точка будет занимать на плоскости определенное положение. В этом случае естественно координаты x , y движущейся точки считать функциями

времени t .

Параметр t может иметь и геометрическое значение (угол, расстояние и т.д.) в зависимости от данного геометрического происхождения кривой.

1) Эта функция, как известно, не всегда будет однозначной.

312

Все функции F( x, y ) , f ( x ), x( t ), y( t ) , входящие в уравнения кривой той

или другой формы из указанных выше, будем предполагать непрерывными и имеющими производные 1-го, 2-го, а в нужных случаях и высшего порядков по соответствующим аргументам.

Если левая часть уравнения (13.1) является алгебраической функцией координат x и y , то линия, им изображаемая, называется алгебраической

линией. В этом случае левую часть уравнения можно считать приведенной к целому рациональному виду, т.е. F( x, y ) можно считать многочленом

относительно x и y . Степень (наивысшая) многочлена F( x, y ) называется

порядком линии, определяемой уравнением (13.1). Если кривая (13.1) и прямая Ax + By + C = 0 даны в одной и той же системе координат, то система уравнений

F(x, y)= 0,

будет иметь число решений, равное степени первого уравнения.

Ax + By + C = 0

Таким образом, порядок линии определяет максимальное число ее точек пересечения с произвольной прямой. Порядок линии является ее инвариантным свойством, не зависящим от того, к какой именно декартовой системе координат отнесена линия.

Общее уравнение кривой порядка n содержит один свободный член, два члена с первыми степенями x и y , три члена 2-й степени, …, n +1 членов n -й

степени, всего:

1 + 2 + 3 + ... +( n +1) = (n +1)(n + 2)

2

выбираемых точек указанное их число может оказаться недостаточным для определения единственной линии n -го порядка, содержащей все эти точки.

Так как два уравнения

F( x, y ) = 0 , f ( x, y ) = 0 ,

одно из которых степени n , другое степени m , имеют, как известно, nm

решений, то линия порядка n пересекает линию порядка m в nm точках. Если же окажется, что две линии указанных порядков имеют число общих точек, большее чем nm , то это обстоятельство означает, что одна из этих линий или обе распадаются, т.е. левые части их уравнений имеют общий множитель в виде рациональной функции от x и y . Действительно, для определения, например,

абсцисс точек пересечения мы должны исключить y из уравнений данных линий

В результате чего получим уравнение вида

R( x ) = 0

313

степени nm (левая часть этого уравнения будет результантом). Если число точек пересечения данных линий больше nm , то результант должен тождественно обращаться в нуль (при всяком x ). Но если результант тождественно равен нулю, то два уравнения наших линий имеют общие решения относительно y при любом

x ; такие общие решения могут быть выделены способом последовательных делений, т.е. F (x, y) и f (x, y) имеют общий рациональный множитель, и данные

кривые распадаются.

13.2 О касательных и нормалях

Умножим обе части полученного равенства на ∆t :

Если уравнение кривой дано в форме F( x, y ) = 0 , то

314

и вставив вместо dx и dy им пропорциональные выражения X − x и Y − y ; таким

способом опять получаем:

(X − x)ддFx + (Y − y)ддFy = 0 .

Если уравнение кривой дано в полярных координатах r = f (θ), то, пользуясь формулами x = r cos θ, y = r sinθ, получим параметрические уравнения кривой

то уравнение касательной (13.12) становится неопределенным; точки кривой, удовлетворяющие указанным условиям, называются ее особыми точками.

Допустим далее, что при параметрическом изображении кривой

Уравнение секущей через точку (x0 ; y0 ) примет вид

315

Если p > q , то уравнение (13.13) при переходе к пределу даст

X − x0 = 0 ,

т.е. уравнение касательной, в данном случае параллельной оси Oy .

Если p < q , то уравнение (13.13) при переходе к пределу даст

Y − y0 = 0 ,

т.е. уравнение касательной, параллельной оси Ox .

Таким образом, при параметрическом изображении кривой уравнениями (13.5), где x(t) и y(t) - функции, однозначные и разложимые вблизи t = t0 по

формуле Тейлора, мы всегда получаем единственную определенную касательную для каждого значения параметра t0 , для которого указанные условия

выполняются.

2 Нормаль

Назовем нормалью к кривой в точке M (x; y) прямую, проходящую через

выбранную точку кривой перпендикулярно к ее касательной в той же точке.

Запишем условие перпендикулярности двух лучей с угловыми коэффициентами k и k1

1 + kk1 = 0

или

k1 = − 1k .

Далее, по угловому коэффициенту касательной составим угловой коэффициент нормали, а затем и само уравнение нормали.

Если кривая определяется уравнениями одной из указанных выше форм (13.1), (13.2), (13.5), то угловой коэффициент касательной будет иметь одно из следующих выражений:

316

дF

13.3 Кривизна линий. Радиус и центр кривизны. Натуральное уравнение кривой

Всякую линию, отличную от прямой, мы называем кривой. Сравнивая кривую с ее касательной в какой-либо ее точке, будем говорить, что кривая в этой точке имеет большую или меньшую кривизну, если она вблизи рассматриваемой точки быстрее или медленнее удаляется от прямой – своей касательной. Постараемся дать точное математическое определение кривизны кривой и выбрать какое-либо определенное число, как характеристику, как меру кривизны кривой в рассматриваемой ее точке.

Простейшей кривой, хорошо нам знакомой, является окружность; при этом очевидно, что окружность вполне можно признать за линию с неизменной (одинаковой) кривизной во всех ее точках, т.к. любая дуга окружности, взятая вблизи какой-либо ее точки без изменения, вполне совмещается со всякой другой частью той же окружности (при равных длинах дуг).

Окружность независимо от места, занимаемого ею на плоскости, вполне определяется своим радиусом, поэтому ее радиус мог бы служить и характеристикой ее кривизны, т.е. чем больше радиус, тем меньшую кривизну она имеет и наоборот, чем меньше радиус

Рисунок 106

317

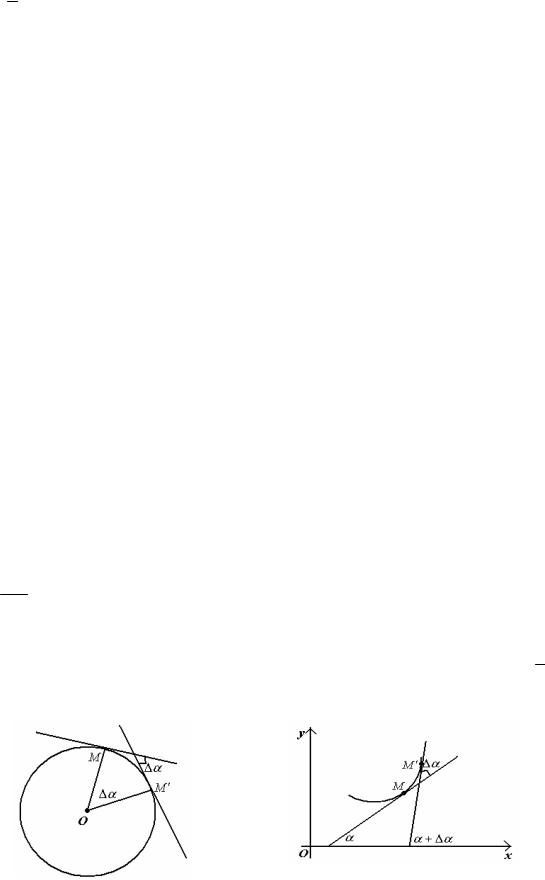
окружности, тем больше ее кривизна. Поэтому совершенно естественно за меру кривизны окружности в каждой ее точке выбрать обратную величину радиуса,

именно 1r .

За направление кривой в каждой ее точке будем считать направление ее касательной в этой точке. Тогда за характеристику кривизны кривой на некотором ее участке можем считать большее или меньшее уклонение касательной в конечной точке участка от касательной в начальной ее точке. Пусть достаточно близкие точки M и M ′ заданной кривой ограничивают дугу MM ′ = ∆s . Назовем угол между касательными в этих точках углом смежности, обозначим его ∆α

(рисунок 106). Тогда выражение

∆α

∆s

может быть названо средней кривизной кривой на протяжении ее дуги ∆s . Очевидно, чем меньше ∆s , тем лучше это отношение будет характеризовать кривизну кривой вблизи начальной точки M ; поэтому кривизной кривой в точке M назовем предел этого отношения, когда точка M ′ неограниченно приближается к точке M , или, что то же самое, когда ∆s стремится к нулю. Итак, за кривизну K кривой в точке M примем выражение:

∆∆αs .

Нетрудно убедиться, что это определение кривизны кривой дает, в частности, для окружности ту же характеристику ее кривизны, какую мы выбрали для нее выше. Действительно, угол (рисунок 107) двух близких касательных равен углу нормалей кривой в соответствующих точках; но для окружности ее дуга ∆s равна радиусу, умноженному на соответствующий центральный угол (угол двух

нормалей), т.е.

∆s = r∆α .

Поэтому

∆∆αs = 1r .

Таким образом, для окружности средняя кривизна любого ее участка постоянна и равна обратной величине ее радиуса. То же значение 1r будет иметь для окружности предел указанного отношения, когда ∆s → 0

Рисунок 107

318