Unlock-Линейная алгебра Сикорская 1

10.2 Ортогональные вектора. Система ортогональных векторов

Пусть дано произвольное n -мерное евклидово пространство En , т.е. в n -

мерном линейном пространстве произвольным способом введено скалярное умножение. Векторы a и b называются ортогональными, если их скалярное произведение равно нулю,

( a, b ) = 0 .

Очевидно, что нулевой вектор ортогонален любому вектору, т.е.

( 0, a ) =( 0, b ) = 0 .

Система векторов называется ортогональной системой, если все векторы этой системы попарно ортогональны между собой.

Теорема 10.1 Всякая ортогональная система ненулевых векторов

Скалярно умножая обе части этого равенства на вектор ai , 1 ≤ i ≤ k , ввиду I, II и IV аксиом, получаем:

0= (0, ai ) = (α1a1 +α2a2 + ... +αk ak , ai )=α1(a1, ai ) +α2 (a2 , ai ) + ... +

+αk ( ak , ai ) =αi ( ai , ai ) .

Отсюда, так как ( ai , ai ) > 0 по IV, вытекает, что нулю может быть равен только коэффициент αi = 0 , i =1,2, ..., k . Таким образом, условие (*) выполняется

евклидова пространства En к ортогональной системе, также состоящей из k

ненулевых векторов b1 , b2 , ..., bk

Положим b1 = a1 , а вектор b2 отличен от нуля. Пусть b2 = α1b1 + a2 . Так как векторы a1 и a2 линейно независимы, то вектор b2 отличен от нуля при любом числе α1 . Подберем это число из условия, что вектор b2 должен быть ортогонален к вектору b1 :

0 = (b1 , b2 )= (b1 , α1b1 + a2 )=α1(b1 , b1 )+ (b1 , a2 ),

откуда,

249

является линейной комбинацией векторов a1 , a2 , ..., ai . Это предположение будет выполняться тогда и для вектора bl +1 , если он будет выбран в виде

bl +1 =α1b1 +α2b2 + ... +αl bl + al +1 .

Вектор bl +1 будет при этом отличен от нуля, так как система (10.5) линейно независимая, а вектор al +1 не входит в записи векторов b1 , b2 , ..., bl . Коэффициенты αi , i =1, 2, ..., l , подберем из условия, что вектор bl +1 должен быть ортогонален ко всем векторам bi , i =1, 2, ..., l :

0= (bi , bl +1 )= (bi ,α1b1 +α2b2 + ... +αlbl + al +1 )=α1(bi , b1 )+α1(bi , b2 )+ ... +

+α1(bi , bl )+ (bi , al +1 );

Продолжая этот процесс, мы построим искомую ортогональную систему b1 , b2 , ..., bk .

Применяя процесс ортогонализации к произвольному базису пространства En , мы получим ортогональную систему из n ненулевых векторов, т.е. ортогональный базис. При этом становится очевидным следующее утверждение.

Всякое евклидово пространство обладает ортогональными базисами, причем любой ненулевой вектор этого пространства входит в состав некоторого ортогонального базиса.

10.3 Норма вектора евклидова пространства

Нормой вектора евклидова пространства называется арифметическое

Норма вектора обладает следующими свойствами.

1 x = 0 тогда и только тогда, когда x = 0 .

2αx = α x , где α - действительное число.

3(x, y) ≤ x y .

4 x + y ≤ x + y .

Докажем эти свойства

250

1Из аксиомы IV скалярного произведения следует, что x > 0 для x ≠ 0

и x = 0 при x = 0 .

3 Так как x + y 2 ≥ 0 , то

0 ≤ x +αy 2 =( x +αy, x +αy ) =( y, y )α2 + 2( x, y )α +( x, x ).

Эту сумму рассматриваем как квадратный трехчлен относительно α . Поскольку указанный трехчлен сохраняет знак, его дискриминант неположителен, т.е.

которое называют неравенством Коши-Буняковского. 4 Используя неравенство (10.7), получаем

x + y 2 =( x + y, x + y ) =( x,x )+2( x, y )+( y, y ) ≤ x 2 +2x y + y 2 =(x + y)2 ,

откуда

Неравенство (10.8) называется неравенством треугольника.

Например, запишем норму и неравенства (10.7), (10.8) для векторов (элементов) евклидовых пространств.

1 В евклидовом пространстве V3 с обычным определением скалярного произведения норма вектора совпадает с его длиной, т.е. a = a ; это следует из формулы (10.6). Неравенства (10.7) и (10.8) принимают соответственно вид

( a, b ) ≤ a b , a + b ≤ a + b .

Отметим, что неравенство a + b ≤ a + b следует из определений суммы

векторов и длины вектора; оно имеет простой геометрический смысл (в треугольнике сумма длин двух сторон больше длины третьей стороны).

В евклидовом пространстве En со скалярным произведением норма элемента x =( x1 , x2 , ..., xn ) определяется формулой

x= 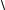x12 + x22 + ... + xn2 ,

анеравенства (10.7) и (10.8) принимают вид

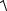(x1 + y1 )2 + (x2 + y2 )2 + ... + (xn + yn )2 ≤

251

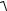≤ x12 + x22 + ... + xn2 + 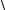y12 + y22 + ... + yn2 .

10.4 Угол между двумя векторами евклидова пространства

Из неравенства Коши-Буняковского получаем

угла. Углом между двумя векторами x и y евклидова пространства называется угол ϕ, для которого

Отметим, что в пространстве V3 всех свободных векторов введенное понятие угла совпадает с понятием угла, рассматриваемого в векторной алгебре.

10.5 Ортонормированный базис

Вектор a называется нормированным, или единичным, если a =1 Если a - ненулевой вектор, то каждый из векторов

будет нормированным. Нахождение для данного вектора нормированного вектора по формуле (10.10) называется нормированием данного вектора, а множитель

µ = ± 1a - нормирующим множителем.

Система векторов e1 , e2 , ..., en называется ортонормированной, если она

где i, k =1, 2, ..., n .

Базис n -мерного евклидова пространства называется ортонормированным, если базисные векторы образуют ортонормированную систему. Рассмотрим теорему о возможности выбора ортонормированного базиса в евклидовом пространстве.

Теорема 10.2 Во всяком евклидовом n -мерном пространстве (n ≥ 2) существует ортонормированный базис.

Доказательство этой теоремы основано на, описанном выше, способе перехода от любой линейной независимой системы векторов евклидова пространства En к ортогональной системе.

252

пространства, то любой вектор x этого пространства можно представить в виде x = x1e1 + x2e2 + ... + xnen ,

Последняя формула упрощается в случае ортонормированного базиса; при этом (ek , ek )=1.

10.6Выражение скалярного произведения через координаты векторов

вортонормированном базисе

Пусть в n -мерном евклидовом пространстве фиксирован ортонормированный базис e1 , e2 , ..., en и даны векторы этого пространства

x = x1e1 + x2e2 + ... + xnen , y = y1e1 + y2e2 + ... + ynen .

Найдем скалярное произведение этих векторов. Принимая во внимание

= x1 y1( e1 , e1 ) + x2 y2 ( e2 , e2 ) + ... + xn yn ( en , en ) = = x1 y1 + x2 y2 + ... + xn yn ,

Итак

( x, y ) = x1 y1 + x2 y2 + ... + xn yn .

т.е., скалярное произведение двух векторов, заданных координатами в ортонормированном базисе, равно сумме произведений одноименных координат.

253

Очевидно,

векторов этого базиса нужно построить ортонормированный базис того же пространства.

Решение. Сначала построим в заданном пространстве какой-нибудь

евклидовым пространством или унитарным пространством, если в нем введено скалярное умножение элементов, т.е. указано правило, ставящее в соответствие любым двум элементам x и y комплексное число (будем обозначать его ( x, y ) и называть эрмитовым произведением элементов x и y ), причем это правило удовлетворяет для любых x, y, z из R и любого

комплексного числа α следующим требованиям (аксиомам эрмитового произведения):

1)( x, y ) = ( y, x ).

2)(x + y, z)=( x, z ) +( y, z ) .

3)(λx, y)= λ( x, y ).

254

4) ( x, x ) > 0 , если x ≠θ и (x, x)= 0 , если x =θ .

Отметим, что аксиома 1) отличается от соответствующей аксиомы I для вещественного евклидова пространства. Из аксиом 1) – 3) следует, что

(x, λy)= λ( x, y )

и ( x, y + z ) =( x, y ) +( x, z ) .

Докажем, что для скалярного произведения в комплексном евклидовом пространстве (т.е. для эрмитового произведения) нельзя сохранить без изменения аксиомы скалярного произведения, принятые в вещественном евклидовом пространстве.

Доказательство. Предположим, что в комплексном линейном пространстве введено скалярное произведение, удовлетворяющее аксиомам I – IV. Тогда из аксиом I и III следует, что для любого числа α и любого элемента x имеет место равенство

(αx, αx)=α(x,αx)=α(αx, x)=α2 (x, x).

Положив α =i , получим (ix, ix)= −( x, x ) < 0 , если x ≠θ .

Таким образом, пришли к противоречию с аксиомой IV, в силу которой скалярный квадрат любого элемента линейного пространства должен быть неотрицательным. Следовательно, в комплексном линейном пространстве нельзя сохранить без изменения аксиомы скалярного произведения, принятые в действительном евклидовом пространстве. Как уже отмечалось, при переходе от действительного к комплексному евклидову пространству видоизменяется

(x + y, z)= (x1 + y1 )z1 + (x2 + y2 )z2 ;

(x, z)+( y, z ) = x1 z1 + x2 z2 + y1 z1 + y2 z2 = (x1 + y1 )z1 + (x2 + y2 )z2 . Следовательно, ( x + y, z ) = ( x, z ) +( y, z ).

Далее, так как

(λx, y)= λx1 y1 + λx2 y2 = λ(x1 y1 + x2 y2 )= λ( x, y ),

то аксиома 3) выполняется.

Теперь покажем выполнимость аксиомы 4):

255

поставлено в соответствие число

( x, y ) = x1 y1 + x2 y2 .

Данное пространство с введенной таким образом операцией не является унитарным, так как аксиома 1) не соблюдается.

Действительно

( y,x ) = y1x1 + y2 x2 = y1x1 + y2 x2 = y1 x1 + y2 x2 .

Следовательно, ( x, y ) ≠ ( y, x ).

Понятия длины вектора и ортогональности векторов в унитарном пространстве вводятся так же как и соответствующие понятия в евклидовом

пространстве, причем обозначения сохраняются, т.е. x = (x, x)= x2 ; вектор x

ортогонален вектору y , если (x, y)= 0 .

Например, в пространстве C 2 , рассмотренном в примере 1), найдем дину вектора a =( 2; 2 −i ) и эрмитово произведение (a, b), если b =( 3 +i; 2 ).

Решение. Так как, согласно определению скалярного произведения,

(a, a)= a2 = 2 2 +( 2 −i )( 2 +i ) = 9 ,

то a = 3 .

Найдем теперь эрмитово произведение векторов a и b, имеем

( a, b ) = 2(3 +i)+( 2 −i )2 = 2( 3 −i ) + 4 −2i =10 −4i .

Теорема 10.3 Эрмитово произведение двух векторов в ортонормированном базисе унитарного пространства равно сумме произведений координат первого вектора на соответствующие сопряженные координаты второго вектора.

256

X Y T = ∑n αk βk . k =1

Таким образом, ( x, y ) = X Y T .

Следствие. Длина вектора, заданного в ортонормированном базисе унитарного пространства, равна корню квадратному из суммы квадратов модулей его координат.

10.8 Изоморфизм евклидовых (унитарных) пространств

Евклидовы пространства E и E′ называются изоморфными, если между векторами этих пространств можно установить такое взаимно однозначное соответствие, что выполняются следующие требования:

1)это соответствие является изоморфным соответствием между E и E′, рассматриваемыми как линейные пространства;

2)при этом соответствии сохраняется скалярное произведение; иными

словами, если образами векторов a и b из E служат соответственно векторы a′ и b′ из E′, то

(a, b)= (a′, b′). (10.12)

Из условия 1) сразу следует, что изоморфные евклидовы пространства имеют одну и ту же размерность. Докажем обратное утверждение:

Ставя в соответствие всякому вектору

n

a= ∑αiei

i=1

из E вектор

n

a′ = ∑αiei′

i =1

из E′, имеющий в базисе (10.14) те же координаты, что и вектор a в базисе (10.13), мы получим, очевидно, изоморфное соответствие между линейными пространствами E и E′. Покажем, что выполняется и равенство (10.12): если

257

n

то (a, b)= ∑αi βi = (a′, b′),

i =1

Естественно изоморфные евклидовы пространства не считать различными. Поэтому для всякого n существует единственное n -мерное евклидово пространство в том же смысле, в каком для всякого n существует единственное n -мерное действительное линейное пространство.

Примем без доказательства утверждение о том, что все сказанное выше об изоморфизме евклидовых пространств переносится и на изоморфизм унитарных пространств.

10.9 Унитарные матрицы

При рассмотрении комплексных евклидовых (т.е. унитарных) пространств аналогом ортогональных матриц выступают унитарные матрицы. Унитарная матрица U = (uij ) - это матрица перехода от одного ортонормированного базиса,

пространства Tn* , равно нулю при i ≠ j и равно 1 при i = j . Таким же свойством обладают строки унитарной матрицы.

2) U −1 =U T , где U T - матрица, которая получается из матрицы U путем транспонирования и замены всех элементов на комплексно сопряженные (индекс

Tозначает транспонирование, а черта – комплексное сопряжение). Матрица U T называется эрмитово сопряженной по отношению к матрице U и обозначается

U* . Таким образом, свойство 2) можно записать так:

U −1 =U * ,

или, в эквивалентных формах:

Аналогично ортогональным матрицам свойства 1) и 2) являются характеристическими свойствами унитарных матриц.

258