
Unlock-Линейная алгебра Сикорская 1
.pdf
Доказательство. Действительно, если векторы a, b , c компланарны, то
они линейно зависимы. В этом случае определитель, составленный из координат векторов, равен нулю, поэтому равно нулю смешанное произведение векторов. Если среди векторов один нулевой, то произведение равно нулю по определению.
Обратно, если смешанное произведение векторов равно нулю, то равен нулю определитель, составленный из координат векторов. Последнее означает
линейную зависимость векторов a, b , c . Векторы a, b , c становятся
компланарными, в частности, какие-то из этих векторов могут быть нулевыми.
Следовательно, условие компланарности трех векторов в координатной форме имеет вид:
a, |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
a1 |
a2 |
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
компланарны |
b1 |
b2 |
b3 |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 |
c2 |
c3 |
|
|
a = {2,5,7}, |
|
|
= {1,1,−1}, |
c = {1,2,2} |
|||||||||
Например, покажем, что |
векторы |
|
|
|
|||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||
компланарны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. Находим смешанное произведение векторов: |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
2 |
5 |
7 |
|
|
1 |
−1 |
|
1 −1 |
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
(a, |
|
|
|
, c )= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 1 −1 |
|
= 2 |
− 5 |
+ 7 |
|
= 8 −15 + 7 = 0. |
|
|
|
|||||||||||||||||||||||
b |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
2 |
|
|
2 |
2 |
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как (a, |
|
|
, c )= 0 , то заданные векторы компланарны. |
|
|
|
|||||||||||||||||||||||||||||
b |
|
|
|
||||||||||||||||||||||||||||||||
Теорема 6.3 Смешанное произведение (a, |
|
, c ) равно объему |
|||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||
параллелепипеда, построенного на векторах a, |
|
, |
c , взятому со знаком «+», если |
||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||
тройка a, |
|
, c - правая, со знаком «-», если тройка a, |
|
, c - левая. |
|
|
|
||||||||||||||||||||||||||||
b |
b |
|
|
|
|||||||||||||||||||||||||||||||
Доказательство. |
Пусть |
даны |
некомпланарные |
|
|
векторы |
a, |
|
, c , |
||||||||||||||||||||||||||
|
|
b |
|||||||||||||||||||||||||||||||||
образующие правую тройку. Обозначим через V объем параллелепипеда, построенного на этих векторах, через S – площадь параллелограмма,
построенного на векторах b , c , а через h – высоту параллелепипеда (рисунок 34).
Рисунок 34
Тогда по определению скалярного и векторного произведений имеем: a [b , c ]= a 
 [b ,c ]cos θ = a
[b ,c ]cos θ = a 
 b
b 
 c sinϕcos θ =
c sinϕcos θ =
= b 
 c sinϕa cos θ,
c sinϕa cos θ,
149
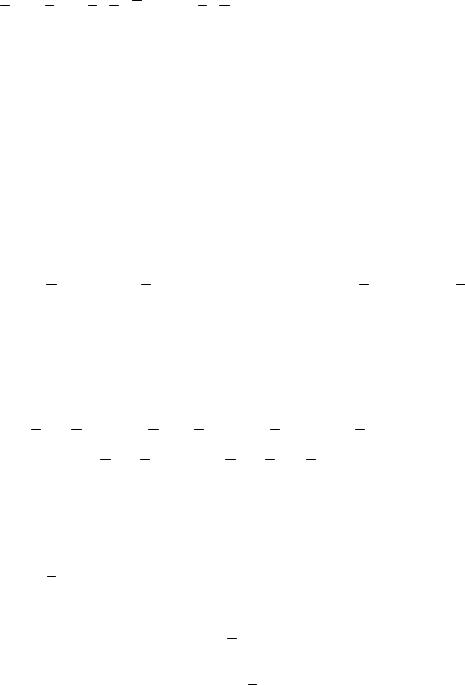
где ϕ - угол между векторами |
|
, c , а θ |
- угол между векторами a и [ |
|
, c ]. Так |
|||||||||||||||||||||||
b |
b |
|||||||||||||||||||||||||||
как |
|
|
|
|
c |
|
|
|
sin ϕ = S, |
|
a |
|
cosθ = h , то a [ |
|
, |
c ]= Sh =V . Если тройка a, |
|
, c - левая, |
||||||||||
|
b |
|
|
|
|
|
b |
b |
||||||||||||||||||||
то h = |
|
a |
|
cos(π −θ) |
|
= |
|
− |
|
a |
|
cosθ . Поэтому a [ |
|
, c ]= −Sh = −V . |
||||||||||||||
|
|
|
|
|
|
b |
||||||||||||||||||||||
Свойства смешанного произведения векторов
1. Смешанное произведение векторов не изменяется при круговой перестановке векторов-сомножителей, то есть
(a, b , c )= (c, a, b )= (b , c, a ).
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.
2. |
|
|
|
|
Смешанное произведение меняет знак на противоположный, если |
|||||||||||||||||||||||||
поменять местами любые два сомножителя, то есть |
|
|
||||||||||||||||||||||||||||
( |
|
, |
|
|
|
|
)= −( |
|
, |
|
|
, |
|
|
). |
|
|
|
|
|
|
|||||||||
|
|
b |
, |
|
|
b |
|
|
|
|
|
|
||||||||||||||||||
a |
c |
a |
c |
|
|
|
|
|
|
|||||||||||||||||||||
3. |
|
|
|
|
Числовой |
множитель |
можно выносить |
за знак |
смешанного |
|||||||||||||||||||||
произведения, то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(λ |
|
, |
|
, |
|
)= λ( |
|
, |
|
, |
|
) (λ R). |
|
|
|
|||||||||||||||
|
b |
b |
|
|
|
|||||||||||||||||||||||||
a |
c |
a |
c |
|
|
|
||||||||||||||||||||||||
Действительно, |
|
|
|
|
обозначим |
[ |
|
, c ]= е |
и |
используя |
свойство |
|||||||||||||||||||
|
|
|
|
b |
||||||||||||||||||||||||||
ассоциативности скалярного произведения относительно умножения на число, получим
(λa, b , c )= (λa)[b , c ]= (λa)e = λ(ae) = λ(a, [b , c ]) = λ(a, b , c ).
4. |
|
Смешанное |
|
произведение |
векторов |
дистрибутивно относительно |
|||||||||||||||||
сложения векторов, то есть |
|
|
|
|
|
|
|||||||||||||||||
( |
|
+ |
|
, |
|
, |
|
)= ( |
|
, |
|
, |
|
)+ ( |
|
, |
|
|
|
). |
|
|
|
|
b |
d |
d |
b |
, d |
|
|||||||||||||||||
a |
c |
a |
c |
c |
]= е, |
|
|||||||||||||||||
Действительно, |
|
обозначим |
[c, |
|
тогда используя свойство |
||||||||||||||||||
|
d |
||||||||||||||||||||||
дистрибутивности скалярного произведения, имеем
(a + b , c, d )= ((a + b ),[c, d ]) = (a + b )e = ae + b e =
= (a,[c, d ]) + (b ,[c, d ]) = (a, c, d )+ (b , c, d ).
5. Геометрический смысл модуля смешанного произведения трех некомпланарных векторов: модуль смешанного произведения трех
некомпланарных векторов численно равен объему параллелепипеда, построенного |
||||||||||||||||||||||||||
на этих векторах, отложенных от одной точки, как на ребрах, то есть |
||||||||||||||||||||||||||
|
(a , |
|
, |
c |
) |
|
|
=Vпар−да. |
|
|
(6.11) |
|||||||||||||||
|
b |
|
|
|
||||||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
V |
|
|
|
|
= |
|
1 V |
|
= |
1 |
|
(a , |
|
, |
|
) |
|
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
b |
c |
|||||||||||||||||||
|
|
призмы |
|
|
|
2 |
пар |
−да |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
V |
|
|
|
|
|
|
|
= |
1 V |
|
|
= |
1 |
|
(a , |
|
, |
c |
) |
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
тетраэдра |
пар−да |
b |
||||||||||||||||||||||||
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
150
6.9 Вопросы для самоконтроля
1Сформулируйте определение вектора.
2Какие векторы называются коллинеарными?
3Какие два вектора называются равными?
4Объясните суть правила сложения векторов.
5Какие три вектора называются компланарными?
6Дайте определение проекции вектора на ось.
7Чему равна проекция суммы нескольких векторов на ось?
8Является ли вектор a = a1 − a2 линейной комбинацией системы векторов
a1, a2 , a3 ?
9Сформулируйте определение линейнозависимой системы векторов.
10Сформулируйте определение линейно независимой системы векторов.
11Верно ли утверждение: любые пять векторов в трехмерном пространстве линейно зависимы?
12Сформулируйте определение максимально линейно независимой системы векторов.
13Дайте определение базиса системы векторов.
14Что означает базис на плоскости; в пространстве?
15Что означает координаты вектора в базисе {e1, e2 , e3}?
16Как сложить (вычесть) два вектора, заданные своими координатами в некотором базисе? Как умножить вектор на число?
17Напишите необходимое и достаточное условие коллинеарности двух векторов. Как оно записывается в координатной форме?
18Какие два вектора называются ортогональными?
19Какой базис в пространстве называется ортонормированным?
20Дайте определение скалярного произведения двух ненулевых
векторов.
21Как найти скалярное произведение двух векторов по их координатам в ортонормированном базисе?
22Если угол между векторами 90o, чему равно скалярное произведение этих векторов?
23Напишите формулу для определения угла между двумя векторами.
Может ли угол между векторами равняться: 0 o ; 45 o ; 180 o ; 270 o ?
24Какая тройка векторов называется правой, левой?
25Дайте определение векторного произведения двух неколлинеарных векторов. Перечислите основные свойства векторного произведения.
26Запишите формулу для нахождения векторного произведения векторов, заданных своими координатами.
27Дайте определение смешанного произведения трех векторов.
28Чему равно смешанное произведение трех векторов, если известны их координаты в ортонормированном базисе?
29Сформулируйте условие компланарности трех векторов.
30Как найти объем тетраэдра, построенного на трех векторах как на
ребрах?
151
Глава 7 Аналитическая геометрия на плоскости
7.1 Аффинная и прямоугольная декартовы системы координат. Простейшие задачи
Пусть на плоскости даны точка O и базис {e1 , e2 }.
Совокупность точки O и базиса {e1 , e2 } называется аффинной системой координат на плоскости (или аффинным репером), и обозначается R (O; e1 , e2 ) или Oxy (рисунок 35).
Точка O называется началом координат. Ось, проходящая через точку O и имеющая направление вектора e1 , называется осью Ox или осью абсцисс.
Рисунок 35
Ось, проходящая через точку O и имеющая направление вектора e2 , называется осью Oy или осью ординат.
Пусть на плоскости задан аффинный репер R (O; e1 , e2 ) и любая точка M .
Рассмотрим OM - радиус-вектор точки M и пусть OM = xe1 + ye2 . Координатами точки M относительно аффинного репера R (O; e1 , e2 )
называются координаты радиус-вектора этой точки относительно базиса {e1 , e2 }.
Пишут: M (x, y)R .
Аффинная система координат на плоскости позволяет решать ряд простейших задач. Рассмотрим три из них.
Нахождение координат вектора, заданного координатами начала и
конца
|
|
Пусть в пространстве |
заданы аффинный репер |
R (O; e1 , e2 ) и точки |
||
A(x1, |
y1 )R , B(x2 , y2 )R . Найдем |
координаты вектора |
|
|
относительно базиса |
|
AB |
||||||
{e , e |
2 |
}. |
|
|
|
|
1 |
|
|
|
|
|
|
Чтобы получить координаты вектора, нужно из координат его конца вычесть соответствующие координаты начала, то есть
|
={x2 |
− x1 ; y2 |
− y1 |
}{e , e }. |
(7.1) |
|
AB |
||||||
|
|
|
|
1 |
2 |
|
152
Задача о деление отрезка в заданном отношении
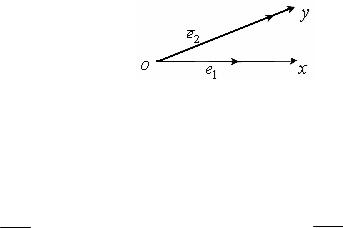
Точка M , принадлежащая прямой M1M 2 , делит отрезок M1M 2 в отношении λ (λ ≠ −1) (рисунок 36), если выполняется векторное равенство:
M1M = λMM2 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 36 |
|
|
|
|
||||||
Если λ > 0 , то |
|
|
|
|
|
↑↑ |
|
|
|
|
|
и говорят, что точка M делит отрезок M1M 2 |
|||||||||||||||||||||||
M1M |
MM2 |
||||||||||||||||||||||||||||||||||
внутренним образом в отношении λ . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Если λ < 0 , то |
|
|
|
↑↓ |
|
|
|
и точка M лежит вне отрезка M1M 2 , но на |
|||||||||||||||||||||||||||
M1M |
MM2 |
||||||||||||||||||||||||||||||||||
прямой M1M 2 , тогда говорят, что |
точка M делит |
отрезок |
M1M 2 внешним |
||||||||||||||||||||||||||||||||
образом в отношении λ . |
|
|
|
|
|
|
|
|
|
|
|
R (O; e1 , e2 ) даны |
|
||||||||||||||||||||||
Пусть |
относительно |
аффинного |
репера |
точки |
|||||||||||||||||||||||||||||||
M1(x1, y1 )R , |
M 2 (x2 , |
y2 )R . Найдем координаты точки |
M , которая делит отрезок |
||||||||||||||||||||||||||||||||
M1M 2 в отношении λ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x = |
x1 + λx2 |
; |
|
y = |
y1 + λy2 |
. |
|
|
|
|
|
|
|
|
|
|
|
(7.2) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 + λ |
|
|
|
|
|
|
|
|
|
|
|
1 + λ |
|
(то |
есть точка M - |
середина |
отрезка |
M1M 2 ), |
||||||||||||||
В частности, |
при λ =1 |
|
|||||||||||||||||||||||||||||||||
имеем: |
x |
+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
- формулы для нахождения координат середины отрезка. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
y1 + y2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Например, пусть даны две точки M1(−1,−2), M2 (3,4). На прямой M1M 2 |
|||||||||||||||||||||||||||||||||||
найдем точку М, которая в три раза ближе к M1 , чем к M 2 |
и находится вне |
||||||||||||||||||||||||||||||||||
отрезка M1M 2 , а также найдем середину этого отрезка. |
|
|
|
||||||||||||||||||||||||||||||||
Решение. Искомая точка М делит отрезок M1M 2 в отношении λ = −1 . По |
|||||||||||||||||||||||||||||||||||
формулам (7.2), считая x1 = −1, y1 = −2, x2 = 3, y2 = 4 |
находим |
|
3 |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
−1 + |
− |
|
|
|
|
|
3 |
|
|
− 2 |
+ |
|
− |
|
|
4 |
|
|
|
|
||||||||||||||
|
3 |
|
3 |
|
|
|
|
|
|||||||||||||||||||||||||||
x = |
|
|
|
|
|
|
|
|
|
|
= −3; y = |
|
|
|
|
|
|
= −5, |
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
− |
|
|
|
|
|
|
||||||||||
|
|
|
1 + |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
153
Таким образом, M (−3,−5) .
С помощью формул для нахождения координат середины отрезка находим точку N –середину отрезка M1M 2
x = −12+ 3 =1; y = − 22+ 4 =1,
Следовательно, N(1,1) - середина M1M 2 .
Совокупность точки O и ортонормированного базиса {i ; j} называется
прямоугольной декартовой системой координат на плоскости (или ортонормированным репером). Обозначается R (O; i , j) (рисунок 37).
Рисунок 37
Очевидно, что прямоугольная декартова система координат является частным случаем аффинной системы координат, поэтому рассмотренные выше определения и простейшие задачи справедливы и в прямоугольной декартовой системе координат.
Нахождение расстояния между двумя точками
Пусть относительно R (O; i , j) заданы точки A(x1, y1 )R и B(x2 , y2 )R , тогда расстояние от точки A до точки B находится по формуле
ρ(A; B)= |
(x |
2 |
− x )2 |
+ (y |
2 |
− y |
1 |
)2 . |
(7.3) |
|
|
1 |
|
|
|
|
7.2 Полярная система координат
При рассмотрении свойств некоторых геометрических фигур иногда используют системы координат отличные от аффинной системы координат и ее частных случаев. Одной из таких систем координат является полярная система координат.
Полярной осью называется луч с заданным сонаправленным единичным вектором.
Совокупность точки О (полюса), полярной оси с началом в этой точке и единичным вектором е называется полярной системой координат.
Зададим на плоскости полярную систему координат с началом в точке О (рисунок 38). Тогда каждой точке М плоскости за исключением точки О ставится
154

в соответствие два числа: ρ = ОМ и ϕ = (e, OM ) , которые называются
полярными координатами.
Рисунок 38
Значения ρ, ϕ изменяются в пределах: 0 < ρ < ∞, −π <ϕ ≤π .
И наоборот, каждой паре чисел (ρ,ϕ) , где 0 < ρ < ∞, −π <ϕ ≤π , отвечает
единственная точка плоскости.
Зададим на плоскости дополнительно прямоугольную декартову систему координат R(O, i , j) . Совместим начало обеих систем координат и направим ось
абсцисс по направлению полярной оси.
Каждая точка плоскости будет иметь в этом случае одновременно прямоугольные декартовы и полярные координаты (рисунок 39)
Рисунок 39
Имеем ОМ = xi + yj . Умножим правую и левую части этого равенства на вектора i , j , учтем при этом, что i = e , тогда получаем:
x = OM e = OM 
 e cos(OM ,e) = ρcosα ,
e cos(OM ,e) = ρcosα ,
y =OM j = OM 
 j cos(OM , j) = ρcos(900 −α) = ρsinα .
j cos(OM , j) = ρcos(900 −α) = ρsinα .
Следовательно, если известны полярные координаты точки, то
соответствующие прямоугольные декартовы координаты находятся по формулам |
||
x = ρcosα, |
(7.4) |
|
y = ρsinα. |
||
|
||
Несложно решается обратная задача. Пусть известны прямоугольные |
||
155
декартовы координаты точки M (x, y) , найдем ее полярные координаты. Так как
ρ = OM и ОМ = xi + yj , то
ρ = x2 + y 2 . |
|
|
|
|
|
(7.5) |
|
Учитывая предыдущие формулы, получаем: |
|
|
|||||
cosα = x = |
x |
, sin α = |
y |
= |
y |
, |
(7.6) |
ρ |
x2 + y 2 |
|
ρ |
|
x2 + y 2 |
|
|
откуда однозначно находится значение α , удовлетворяющее условиям
−π <α ≤π .
Например, найдем декартовы координаты точки М, полярные координаты
которой 5, 23π .
Решение. По формулам (7.4) вычисляем:
x = ρ cosα = 5 cos |
2π |
= − |
5 |
, |
|
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
y = ρ sin α = 5 sin |
2π |
= 5 |
3 . |
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
5 |
3 |
|
|
|
|
|
|
− |
, |
|
|||
Декартовы координаты точки М таковы: |
2 |
2 |
|
. |
||||||
|
|
|
|
|
|
|
|
|
||
7.3 Преобразование системы координат
При решении многих задач аналитической геометрии наряду с данной прямоугольной системой координат приходится вводить и другие прямоугольные системы координат. При этом, естественно, изменяются как координаты точек, так и уравнения линий. Возникает задача: как, зная координаты точки в одной системе координат, найти координаты этой же точки в другой системе координат. Решить эту задачу позволяют формулы преобразования координат.
Рассмотрим два вида преобразований координат.
Параллельный перенос осей координат
Пусть на плоскости задана прямоугольная система координат Оху. Под
параллельным переносом осей координат понимают переход от системы координат Оху к новой системе О1х1 у1, при этом меняется положение начала
координат, а направление осей и масштаб остаются неизменными.
Пусть начало новой системы координат точка О1 имеет координаты (х0 , у0 ) в старой системе координат Оху, т.е. О1(х0 , у0 ). Обозначим координаты произвольной точки М плоскости в системе Оху через (х, у), а в новой системе О1х1 у1 через (х′, у′) (рисунок 40).
156

Рисунок 40
Рассмотрим векторы
OM = xi + yj, OO1 = x0i + y0 j, O1M = x′i + y′j.
Так как OM =OO1 +O1M , то xi + yj = x0i + y0 j + x′i + y′j , т.е.
xi + yj =(x0 + x′)i +(y0 + y′) j .
Следовательно,
x = x0 + x′,y = y0 + y′.
Полученные формулы позволяют находить старые координаты известным новым x′, y′ и наоборот.
(7.7)
x, y по
Поворот осей координат
Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.
Пусть новая система О1х1 у1 получена поворотом системы Охуна угол α. Пусть М – произвольная точка плоскости (х, у) - ее координаты в старой
системе и (х′, у′) - в новой системе.
Введем две полярные системы координат с общим полюсом О и полярными осями Ох и Ох1 (масштаб одинаков). Полярный радиус ρ в обеих
системах одинаков, а полярные углы соответственно равны α +ϕ и ϕ, где ϕ - полярный угол в новой полярной системе (рисунок 41)
157

Рисунок 41
По формулам перехода от полярных координат к прямоугольным имеем
x =ρcos(α+ϕ), |
x =ρcosϕcosα−ρsinϕsinα, |
|
т.е. |
y =ρsin(α+ϕ), |
y =ρcosϕsinα+ρsinϕcosα. |
|
|
′ |
|
′ |
. Поэтому |
Но ρcosϕ = x , |
ρsinϕ = y |
||||
|
′ |
′ |
|
|
|
x = x cosα− y sinα, |
(7.8) |
||||
|
′ |
′ |
|
|
|
y = x sinα+ y cosα. |
|
||||
Полученные формулы называются формулами поворота осей. Они |
|||||
позволяют |
определить |
′ |
старые координаты x, y произвольной точки М через |
||
|
|
′ |
этой же точки М, и наоборот. |
||
новые координаты x , y |
|
||||
Если новая система координат О1х1 у1 получается из старой Оху путем параллельного переноса осей координат и последующим поворотом осей на угол
α (рисунок 42), то путем |
введения вспомогательной системы О1х1′у1′ легко |
|||
получить формулы |
|
|
|
|
|
′ |
′ |
, |
|
x = x cosα− y sinα+ х0 |
(7.9) |
|||
|
′ |
′ |
, |
|
y = x sinα+ y cosα+ у0 |
|
|||
выражающие старые координаты x, y произвольной точки через ее новые координаты x′, y′.
Рисунок 42
158
