
Unlock-Линейная алгебра Сикорская 1
.pdf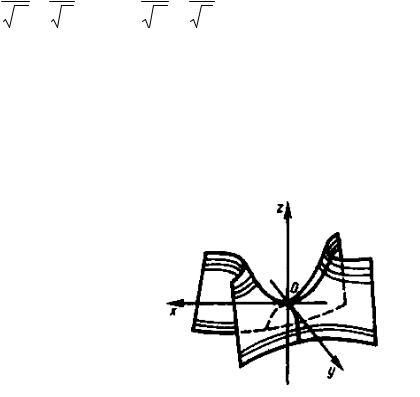
|
x |
− |
y |
= 0, |
|
x |
+ |
y |
= 0, |
|
p |
q |
|
p |
q |
||||
|
|
|
и |
|
|
||||
|
|
z = 0 |
|
|
|
z = 0. |
|
||
|
|
|
|
|
|
||||
Таким образом, рассмотренные сечения позволяют изобразить гиперболический параболоид в виде седлообразной поверхности (рисунок 101). На рисунке изображено несколько сечений параболоида плоскостями z = h для случаев h > 0 и h < 0 .
Точка (0, 0, 0) называется вершиной гиперболического параболоида; числа
р и q — его параметрами.
Рисунок 101
6 Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
x2 |
+ |
y2 |
− |
z2 |
= 0 . |
(8.57) |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
Уравнение (8.57) называется каноническим уравнением конуса второго порядка.
Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Оxz ( у = 0) получаем линию
x2 |
|
z 2 |
|
|
|
|
|
|
|
|
− c2 |
= 0, |
||
a 2 |
||||
|
y = 0, |
|||
|
||||
распадающуюся на две пересекающиеся прямые
x |
|
z |
|
x |
|
z |
|
||
|
|
− |
|
= 0, |
|
|
+ |
|
= 0, |
|
|
|
|
||||||
|
|
и |
|
||||||
a |
|
c |
|
a |
|
c |
|
||
|
y = 0 |
|
y = 0. |
||||||
Аналогично, в сечении конуса плоскостью Оуz (x = 0) также получаются две пересекающиеся прямые
219
y |
|
|
z |
|
|
|
|
|
|
|
|
|
y |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
− c = 0, и |
|
+ c = 0, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
b |
b |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x = 0 |
|
|
|
|
|
|
|
|
|
x = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = h , |
||||||||||||||||
Рассмотрим |
|
|
теперь сечения |
|
данной |
поверхности |
плоскостями |
||||||||||||||||||||||||||||||||
параллельными плоскости Оху. Получим уравнения |
|
|
|||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
y |
2 |
|
|
|
|
||||
|
x |
|
+ |
|
|
|
= |
h |
|
|
, |
|
|
|
|
|
|
|
|
|
|
+ |
|
=1, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
b |
|
|
|
|
|
c |
|
|
или |
|
|
|
|
*2 |
|
b |
*2 |
|
|
|
|
||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
z = h. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = h, |
|
|
|
|
||||||||||||
из которых следует, что при h > 0 |
|
и h < 0 |
в сечениях получаются эллипсы с |
||||||||||||||||||||||||||||||||||||
полуосями a* = |
a |
|
h |
|
|
, |
b* = |
b |
|
h |
|
|
|
. При увеличении абсолютной величины h полуоси |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а* и b* также увеличиваются. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
При |
|
|
h = 0 |
|
|
|
линия |
пересечения поверхности с |
плоскостью |
z = h |
|||||||||||||||||||||||||||||
вырождается в точку (0, 0, 0).
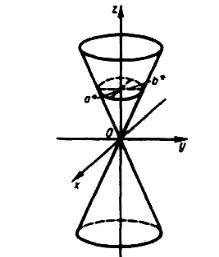
Таким образом, рассмотренные сечения позволяют представить конус в виде поверхности, изображенной на рисунке 102
Рисунок 102
8.11 Вопросы для самоконтроля
1 |
Сформулируйте определение аффинной системы координат в |
|
пространстве. |
|
|
2 |
Сформулируйте определение координат точки |
относительно |
аффинного репера. |
|
|
3 |
Как найти координаты вектора по координатам точек его начала и |
|
конца? |
|
|
4Запишите формулы для нахождения координат точки, делящей отрезок в отношении λ.
5Сформулируйте определение прямоугольной декартовой системы координат в пространстве.
6Запишите формулу для нахождения расстояния между точками.
220
7Запишите уравнение поверхности в прямоугольной декартовой системе координат.
8Запишите уравнение сферы.
9Как определяется уравнение линии в пространстве?
10Запишите уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
11Запишите общее уравнение плоскости в пространстве.
12Как расположены плоскости Ax + D = 0, By + Cz = 0 в пространстве?
13Запишите уравнение плоскости , проходящей через три точки
14Запишите уравнение плоскости «в отрезках».
15По какой формуле определяется угол между плоскостями?
16Запишите условия параллельности и перпендикулярности двух плоскостей.
17По какой формуле можно найти расстояние от точки дот плоскости?
18Запишите параметрические уравнения прямой в пространстве.
19Запишите общее уравнение прямой в пространстве.
20Запишите формулу для нахождения угла между прямыми в пространстве.
21Запишите условия параллельности и перпендикулярности двух прямых в пространстве.
22По какой формуле можно найти угол между плоскостью и прямой?
23Сформулируйте определение цилиндрической поверхности.
24Сформулируйте определение эллипсоида и запишите его каноническое уравнение.
25 Изобразите следующие поверхности |
x2 |
+ |
y 2 |
− |
z 2 |
= 0, |
x2 |
+ |
y2 |
= 2z . |
|
a 2 |
b2 |
c2 |
p |
q |
|||||||
|
|
|
|
|
|
26Какая кривая будет в сечении у двуполостного гиперболоида, если рассечь его плоскостью z = h ?
27Какие поверхности относятся к цилиндрам второго порядка?
28Сформулируйте определение гиперболического параболоида и запишите его каноническое уравнение.
29Какая кривая будет в сечении у конуса второго порядка, если рассечь его плоскостью у = 0 ?
30Какая кривая будет в сечении у эллипсоида, если рассечь его плоскостью z = h ?
221
Глава 9 Линейное пространство. Подпространство линейного пространства
9.1 Понятие линейного пространства
Рассмотрим множество V элементов x, y, z, ... и множество R
действительных чисел. Определим операцию «сложения» элементов множества V (ее называют внутренней операцией): любой упорядоченной паре элементов
x V , y V |
поставим в соответствие третий элемент |
z V , |
называемый |
их |
||||
«суммой», будем писать в этом случае z = x + y . |
|
|
|
|
||||
Введем также операцию «умножения» элементов множества V |
на |
|||||||
действительное |
число (эту операцию называют внешней); каждому |
элементу |
||||||
x V и действительному |
числу α R поставим в |
соответствие |
элемент |
|||||
z =αx = xα , |
где |
z V . Потребуем, чтобы |
операция |
«сложения» элементов |
||||
множества |
V |
и операция |
«умножения» |
элементов |
этого |
множества |
на |
|
действительное число удовлетворяли следующим аксиомам:
I |
Сложение коммутативно, т.е. x + y = y + x для любых x V , y V . |
II |
Сложение ассоциативно, т.е. (x + y)+ z = x + ( y + z) для любых x V , |
y V , z V .
III Существует нулевой элемент, т.е. такой элемент, который в сумме с любым элементом x дает тот же элемент x ; обозначим нулевой элемент символом θ , тогда x +θ = x , для любого x V .
IV Для каждого элемента x V существует противоположный элемент, т.е. такой элемент, который в сумме с данным дает нулевой элемент; элемент,
противоположный элементу x , обозначим |
через − x , |
тогда x + (−x) =θ для |
||
любого x V . |
|
|
т.е. 1 x = x для любого |
|
V Умножение на число 1 не меняет элемента, |
||||
x V . |
|
|
|
|
Для любых x, |
y V , α, β R : |
|
|
|
VI |
α(βx)= (αβ )x . |
|
|
|
VII |
α(x + y)=αx +αy . |
|
|
|
VIII (α + β)x =αx + βx . |
|
|
||
Множество V |
элементов x, y, z, ..., |
в котором |
определены операции |
|
«сложения» элементов и «умножения» элемента на действительное число, удовлетворяющие аксиомам I – VIII, называется действительным линейным пространством (или действительным векторным пространством). Элементы действительного линейного пространства называют векторами.
Обращаем внимание читателя, что внутренняя операция «сложения» на самом деле может и не быть сложением в обычном понимании, а может быть, например, вычитанием, умножением, логарифмированием по определенному основанию и т.д. В точности также дело обстоит и с внешней операцией – «умножением». В дальнейшем, помня это, кавычки для удобства записи будем
222
опускать, однако обязательно будем оговаривать в каждом отдельном случае, что означает в этом конкретном примере операция сложения и что означает операция умножения.
Итак, дано определение действительного линейного пространства. Если бы мы предположили, что в множестве V определено умножение не только на действительные, но и на любые комплексные числа, то, сохраняя те же аксиомы I
– VIII, получили бы определение комплексного линейного пространства. Для определенности ниже рассматриваются действительные линейные пространства, однако все, что будет сказано в настоящей главе, переносится дословно на случай комплексных линейных пространств.
Для линейного пространства справедливы следующие теоремы:
Теорема 9.1 В линейном пространстве имеется единственный нулевой элемент.
Доказательство. Предположим, что в линейном пространстве V имеются два нулевых элемента θ1 и θ2 , тогда θ1 +θ2 =θ1 и θ1 +θ2 =θ2 , поэтому θ1 =θ2 .
Теорема 9.2 Для любого элемента x линейного пространства существует
единственный противоположный элемент − x . |
x |
|
|
Доказательство. Предположим, что для элемента |
существует два |
||
противоположных |
элемента x1 и x2 , т.е. x + x1 =θ |
и |
x + x2 =θ , тогда |
x1 = (x2 + x) + x1 = x2 |
+ (x + x1 ) = x2 , следовательно, x1 = x2 . |
|
|
Теорема 9.3 Для элемента − x противоположным будет элемент x .
Доказательство. Поскольку − x + x = x + (−x) (по аксиоме I) и x +( −x ) =θ
(по аксиоме III), то − x + x =θ , а это означает, что x - элемент, противоположный элементу − x .
Теорема 9.4 Для любого элемента |
x |
произведение 0x =θ , где 0 – число |
||
нуль, θ – нулевой элемент. |
|
|
|
0x = 0x + (x + (−x)) = (0x + x) + (−x) = |
Доказательство. |
Так |
как |
|
|
= x( 0 +1) +( −x ) = x +( −x ) = θ. Итак, получим 0x = θ. |
||||
Теорема 9.5 Для любого элемента |
x |
произведение −1 x = −x , где (− x) - |
||
элемент, противоположный элементу x .
Доказательство. Поскольку −1 x + x = (−1 +1)x = 0x =θ , или −1 x + x =θ , то −1 x - элемент, противоположный элементу x , т.е. (−1)x = −x .
Теорема 9.6 Для любого числа α произведение αθ =θ , где θ – нулевой элемент.
Доказательство.αθ =α(x + (−x)) =α(x + (−1)x) =αx +α(−1)x =αx + + (−αx)=θ , αθ =θ .
223
|
|
Теорема 9.7 Если αx = 0 и α ≠ 0 , то x =θ . |
1 |
|
|
||||
|
|
Доказательство. Пусть αx = 0 и α ≠ 0 , тогда |
αx = 0 , или x =θ . |
||||||
|
|
|
|||||||
|
|
|
|
|
|
|
α |
|
|
|
|
Теорема 9.8 Если αx = 0 и x ≠θ , то α = 0. |
|
|
|
||||
|
|
Доказательство. |
|
Предположим противное, т.е. |
α ≠ 0 , получим |
||||
|
1 |
(αx)= |
1 |
0 = 0 , или |
1 |
αx = x = 0 , то, что противоречит условию. |
|||
α |
α |
α |
|
|
|
||||
|
|
Следствие. Равенство αx = 0 выполняется |
тогда и |
только тогда, когда |
|||||
α = 0 или x =θ . |
|
|
|
|
|
||||
Следствие непосредственно вытекает из 4, 6 – 8.
Примеры линейных пространств:
1) Множество всех свободных векторов a(a1 , a2 , a3 ), где a1 , a2 , a3 могут
принимать любые действительные значения, для которых определены сложение и умножение вектора на число является линейным пространством. Обозначим это линейное пространство символом V3 . Отметим, что роль нулевого элемента здесь
играет нуль-вектор; для любого вектора a противоположным является − a .
2)Множество всех матриц размеров m × n , для которых определены сложение матриц и умножение матрицы на число обычным образом, является
линейным пространством. Роль нулевого элемента здесь играет нулевая матрица; для матрицы (aik )mn противоположной будет матрица (− aik )mn .
3)Множество {Pn (x)} всех алгебраических многочленов степени, не
превышающей натурального числа n , для которых операции сложения многочленов и умножения многочлена на действительное число определены обычными правилами, является линейным пространством. Роль нулевого элемента играет многочлен, все коэффициенты которого равны нулю; для многочлена
Pn (x) = a0 xn + a1 xn−1 +... + an−1 x + an .
противоположным будет
− Pn (x) = −a0 xn − a1 xn−1 −... − an−1 x − an .
4) |
Множество |
An , элементами |
которого |
являются |
упорядоченные |
||
совокупности n действительных |
чисел |
x = (x1, x2 , ..., xn ), |
y = (y1 , y2 , ..., yn ); |
||||
линейные операции над элементами An определяются формулами |
|||||||
x + y = ((x1 + y1 ), (x2 + y2 ), |
..., (xn + yn )), |
|
|
||||
αx = (αx1 , αx2 , ..., αxn ); |
|
|
|
− x = (− x1 , −x2 , ..., − xn ) - |
|||
элемент |
θ = (0, 0,...,0) |
является |
нулевым, элемент |
||||
противоположным элементу x = (x1 , |
x2 , ..., xn ), является линейным пространством. |
||||||
224
9.2 Линейная зависимость векторов
Вектор y называют пропорциональным вектору x , если y = kx для
некоторого числа k . В аналитической геометрии такие векторы называются
коллинеарными. Вектор y называют линейной комбинацией (конечной)
системы векторов x1 , x2 , ..., xs , если существуют такие числа α1 , α2 , ..., αs , что
y =α1x1 +α2 x2 + ... +αs xs . |
(9.1) |
При этом говорят также, что вектор y линейно выражается через векторы
x1 , x2 , ..., xs .
Если вектор b линейно выражается через систему вектора x1 , x2 , ..., xs ,
то он будет линейно выражаться и через любую конечную систему векторов, включающую в себя систему x1 , x2 , ..., xs .
Действительно, если выполняется равенство y =α1x1 +α2 x2 + ... +αs xs + 0 xs +1 + ... + 0 xr .
Это равенство означает, что вектор b линейно выражается через систему векторов x1 , x2 , ..., xr .
Конечная система векторов x1 , x2 , ..., xr называется линейно зависимой, если существуют такие числа α1 , α2 , ..., αr , не все равные нулю, что
α1x1 +α2 x2 + ... +αr xr = 0 . |
(9.2) |
В противном случае система векторов x1 , x2 , ..., xr линейно независима.
Система векторов x1 , x2 , ..., xs линейно зависима тогда и только тогда,
когда хотя бы один из ее векторов линейно выражается через остальные векторы.
Действительно, если система векторов x1 , x2 , ..., xs линейно зависима, то выполняется равенство
α1x1 +α2 x2 + ... +αs xs = 0 , |
|
|
(9.3) |
||||||
в котором, например αs ≠ 0 . Тогда из этого равенства получаем: |
|||||||||
x |
s |
= −α1 x − α2 a |
|
− ... − αs −1 x |
s −1 |
. |
|||
|
αs 1 |
αs |
|
2 |
αs |
|
|
||
Это означает, что вектор xs |
линейно выражается через систему векторов |
||||||||
x1 , x2 , ..., xs −1 . |
|
|
|
|
линейно выражается через систему векторов |
||||
Наоборот, пусть вектор xs |
|||||||||
x1 , x2 , ..., xs −1 , т.е. |
|
|
|
|
|
|
|
||
xs |
=α1x1 +α2 x2 + ... +αs −1xs −1 . |
|
|
||||||
Тогда верно |
и |
равенство (9.3), в котором αs = −1 ≠ 0 . Значит, система |
|||||||
векторов x1 , x2 , ..., xs линейно зависима.
Например, рассмотрим линейное пространство многочленов не выше
второй степени. Докажем, что векторы |
p =1 + 2t + 3t 2 |
, |
p |
2 |
= 2 + 3t + 4t 2 |
и |
|
1 |
|
|
|
|
p3 = 3 + 5t + 7t 2 линейно зависимы.
225
Действительно, эти вектора линейно зависимы, так как p3 =1 p1 +1 p2 .
Совокупность элементов, каждый их которых есть элемент системы x1 , x2 , ..., xn , называется подсистемой этой системы.
Две конечные системы векторов называют эквивалентными, если они линейно выражаются одна через другую.
Непосредственно легко проверить, что
1)эквивалентность систем векторов обладает свойством транзитивности, т.е. если первая система векторов эквивалентна второй, а вторая – третьей, то первая система векторов эквивалентна третьей;
2)если вектор линейно выражается через данную систему векторов, то он линейно выражается через любую другую систему векторов, эквивалентную данной.
Теорема 9.9 (основная теорема о линейной зависимости векторов)
Пусть даны две системы векторов x1 , x2 , ..., xr и y1 , y2 , ..., ys , причем первая
линейно независима и линейно выражается через вторую. Тогда число векторов в первой системе не превышает числа векторов во второй, т.е. r ≤ s .
Доказательство. Утверждение теоремы, по существу, означает, что из s векторов нельзя создать систему линейных комбинаций этих векторов, которая, с одной стороны, линейно независима, а с другой – содержит более s векторов.
По условию теоремы система векторов x1 , x2 , ..., xr линейно независима и
линейно |
|
выражается |
|
через векторы системы y1 , y2 , ..., ys . Следовательно, |
|||||||||||||||||||
существуют такие числа αij , что выполняются неравенства |
|
||||||||||||||||||||||
x |
|
=α |
11 |
y |
+α |
12 |
y |
2 |
+ ... +α |
1s |
y |
s |
, |
|
|
||||||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
x2 =α21 y1 +α22 y2 + ... +α2s ys |
, |
(9.4) |
|||||||||||||||||||||
....................................... |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
r |
=α |
r1 |
y |
+α |
r 2 |
y |
2 |
+ ... +α |
rs |
y |
s |
. |
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Допустим, что r > s , и рассмотрим линейную комбинацию векторов
λ1x1 + λ2 x2 + ... + λr xr .
В силу равенств (9.4) эту линейную комбинацию можно представить следующим образом:
λ1x1 + λ2 x2 + ... + λr xr = ∑i =r1λi xi = ∑i =r1λi ∑j s=1xi y j = ∑j s=1 ∑i =r1 xij λi y j .
В рассматриваемой линейной комбинации векторов попытаемся подобрать числа λ1 , λ2 , ..., λr так, что они одновременно не равны нулю, но при этом все
коэффициенты при векторах y1 , y2 , ..., ys обнуляются. Это означает, что набор чисел λ1 , λ2 , ..., λr является решением системы линейных однородных уравнений
226
α λ |
+α |
12 |
λ |
2 |
+ ... +α |
1r |
λ |
r |
= 0, |
||||||
|
11 1 |
|
|
|
|
|
|
|
|||||||
α |
21λ1 +α22λ2 + ... +α2r λr = 0, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
....................................... |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α λ |
+α |
r 2 |
λ |
2 |
+ ... +α |
rs |
λ |
r |
= 0. |
||||||
|
r1 1 |
|
|
|
|
|
|
|
|
||||||
При r > s число неизвестных в системе превышает число уравнений, поэтому она имеет ненулевое решение. Любое ненулевое решение системы дает такой набор коэффициентов λ1 , λ2 , ..., λr , одновременно не обращающихся в нуль,
для которых
λ1x1 + λ2 x2 + ... + λr xr = 0 .
Существование таких коэффициентов равносильно линейной зависимости векторов x1 , x2 , ..., xr , что противоречит условию теоремы. Значит,
предположение r > s неверно и на самом деле r ≤ s . Что и требовалось доказать.
Следствие. Любые две эквивалентные линейно независимые системы векторов имеют одинаковое число векторов.
Действительно, по доказанной теореме для двух линейно независимых эквивалентных систем векторов количество векторов в первой системе не превышает количества векторов во второй. Но системы в этом утверждении можно поменять местами, поэтому в первой системе не меньше векторов, чем во второй.
Заметим, что любые две максимальные линейно независимые подсистемы данной системы векторов эквивалентны. Значит, согласно доказанному следствию они имеют одно и то же число векторов.
9.3 Размерность и базис линейного пространства
Линейное пространство V называется n -мерным, если в нем существует n линейно независимых векторов, а любые n +1 векторы являются линейно зависимыми. Число n называется в этом случае размерностью линейного пространства V . Итак, число n называется размерностью линейного пространства V , если выполняются следующие условия:
1)в V существует n линейно независимых векторов;
2)любая система n +1 векторов из V линейно зависима.
Размерность линейного пространства V обозначается dimV (от французского слова dimension – размерность). Если пространство состоит из одного нулевого элемента, его размерность считают равной нулю. Введенное понятие размерности согласуется с наглядным представлением о ней; так, пространство V3 всех свободных векторов является трехмерным ( dimV3 = 3 ),
пространство V2 - двумерным, пространство V1 - одномерным.
Базисом n -мерного линейного пространства Vn называется любая упорядоченная система n линейно независимых векторов этого пространства.
227

Линейное пространство, в котором имеется базис, состоящий из конечного числа векторов, называется конечномерным. Примерами конечномерных пространств являются пространства V1 , V2 , V3 , An , рассмотренные выше.
Линейное пространство называется бесконечномерным, если при любом натуральном числе m в нем найдется m линейно независимых векторов.
Примером бесконечномерного пространства будет множество всевозможных действительных функций действительного переменного, если сложение функций и их умножение на действительное число понимать так, как это принято в теории функций, т.е. как сложение или умножение на число значений функций при каждом значении независимого переменного.
Приведем примеры базисов некоторых линейных пространств.
1)Базис пространства V3 образует любая тройка некомпланарных
векторов, так как эти векторы линейно независимы.
2)Базис пространства V2 образуют два любых неколлинеарных вектора,
поскольку они линейно независимы и любой вектор плоскости, определяемый этими двумя векторами, можно разложить по ним.
3) Базисом линейного пространства V1 является любой ненулевой вектор, коллинеарный данной прямой.
4) |
Многочлены p |
0 |
(x)=1, |
p (x) = x , |
p |
2 |
(x) = x2 |
образуют базис в |
|
|
|
1 |
|
|
|
пространстве P2 . Действительно, эти многочлены линейно независимы, и любой
многочлен |
p(x) = a + bx + cx2 из P |
можно представить в виде линейной |
|
2 |
p2 (x). |
комбинации многочленов p0 (x), p1(x), |
||
5)Рассмотрим некоторое линейное пространство An , состоящее из
векторов xi = (xi |
, xi , ..., |
xi ), i = |
|
. Докажем, |
что система |
векторов этого |
1, n |
||||||
1 |
2 |
n |
|
|
||
пространства |
|
|
|
|
|
|
e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0) , …, en = (0, 0, ..., 0, 1) |
(9.5) |
|||||
- линейно независима, а совокупность e1 , e2 , ..., en , |
x , где x = (x1 , |
x2 , ..., xn ) - любой |
||||
элемент этого пространства, образует линейно зависимую систему, т.е. докажем, что векторы e1 , e2 , ..., en образуют базис пространства An . Действительно,
линейная комбинация векторов (9.5) представляет вектор
α1e1 +α2e2 + ... +αn en = (α1 , α2 , ..., αn ),
который является нулевым лишь при α1 =α2 =... =αn = 0 . Это означает, что
векторы (9.5) линейно независимы. Поскольку
x = (x1 , x2 , ..., xn )= x1e1 + x2e2 + ... + xn en
есть линейная комбинация векторов (9.5), то система e1 , e2 , ..., en , x линейно зависима. Следовательно, линейное пространство An будет n -мерным, а система векторов (9.5) образует базис этого линейного пространства.
228
