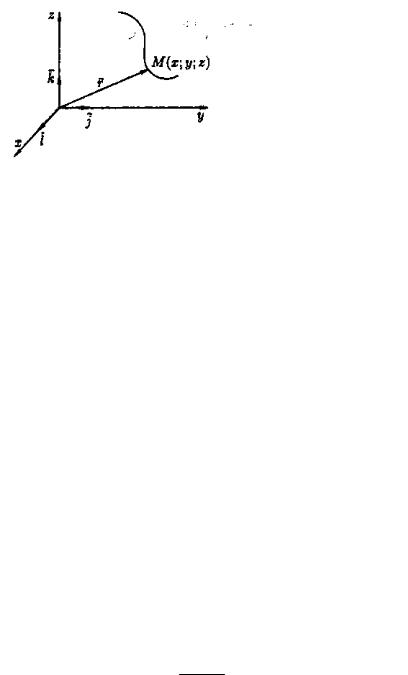6Запишите формулу для нахождения расстояния между точками.
7Какая система координат называется полярной?
8Запишите формулы для нахождения полярных координат точки через прямоугольные декартовые координаты и наоборот.
9Что понимают под параллельным переносом осей координат?
10Что понимают под поворотом осей координат?
11Запишите уравнение линии на плоскости.
12Запишите уравнение прямой с угловым коэффициентом.
13Запишите уравнение прямой, проходящей через две точки.
14 |
Запишите |
формулы для нахождения угла между |
прямыми |
L1 : y = k1 x + b1 и L2 : y = k2 x + b2 . |
|
15 |
Запишите |
условия параллельности и перпендикулярности |
прямых |
L1 : y = k1 x + b1 и L2 : y = k2 x + b2 . |
|
16Какой вид имеет общее уравнение прямой на плоскости?
17Какую прямую определяет уравнение вида Ах + Ву = 0 ?
18Запишите уравнение прямой «в отрезках».
19По какой формуле можно найти расстояние от точки до плоскости?
20Запишите уравнение окружности.
21Сформулируйте определение эллипса.
22Запишите каноническое уравнение эллипса.
23Что называется эксцентриситетом эллипса?
24Дайте определение гиперболы.
25Запишите каноническое уравнение гиперболы.
26Какая гипербола называется равносторонней?
27Запишите формулы для нахождения эксцентриситета и асимптот гиперболы.
28Сформулируйте определение параболы.
29 |
Изобразите |
параболы, |
заданные уравнениями |
у2 = 2 рх, x2 = 2 py , |
( p > 0 ). |
Запишите уравнения эллипса с центром в точке O1(x0 ; y0 ) и полуосями |
30 |
a , b, параллельные осям координат. |
|
|
|
31 |
Запишите уравнения гиперболы с центром в точке O1(x0 ; y0 ), |
действительной осью - a , мнимой осью - b. |
|
|
|
32 |
Уравнение |
Ax2 + Cy2 + Dx + Ey + F = 0 |
и |
его |
геометрическое |
толкование в случае AC > 0 . |
|
|
|
|
33 |
Уравнение |
Ax2 + Cy2 + Dx + Ey + F = 0 |
и |
его |
геометрическое |
толкование в случае AC < 0 . |
|
|
|
|
34 |
Уравнение |
Ax2 + Cy2 + Dx + Ey + F = 0 |
и |
его |
геометрическое |
толкование в случае AC = 0 . |
|
|
|
|
35 |
Общее |
уравнение |
кривой |
второго |
порядка |
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 и его геометрическое толкование.

Глава 8 Аналитическая геометрия в пространстве
8.1 Аффинная и прямоугольная декартовы системы координат. Простейшие задачи
Пусть в пространстве даны точка O и базис {e1 , e2 , е3 }.
Совокупность точки O и базиса {e1 , e2 , е3 } называется аффинной
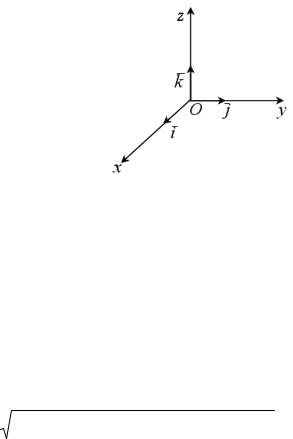
системой координат в пространстве (или аффинным репером), и обозначается R (O; e1 , e2 , е3 ) или Oxyz (рисунок 72).
Точка O называется началом координат. Ось, проходящая через точку O и имеющая направление вектора e1 , называется осью Ox или осью абсцисс.
Рисунок 72
Ось, проходящая через точку O и имеющая направление вектора e2 , называется осью Oy или осью ординат. Ось, проходящая через точку O и имеющая направление вектора e3 , называется осью Oz или осью аппликат.
Выделяют также три плоскости, называемые координатными. Каждая из них содержит по две координатные оси. Обозначаются плоскости следующим образом: Oxy , Oyz,Oxz.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть на плоскости задан аффинный репер R (O; |
e1 , e2 , e3 ) и любая точка |
M . Рассмотрим |
|
- радиус-вектор точки M и пусть |
|
= xe1 + ye2 + ze3 . |
|
OM |
OM |
Координатами |
|
точки |
M |
относительно |
|
аффинного |
репера |
R (O; e1 , e2 , e3 ) называются координаты радиус-вектора этой точки относительно |
базиса {e1 , e2 , e3 }. Пишут: M (x, y, z)R . |
|
|
|
|
|
|
|
|
Так же как и на плоскости, аффинная система координат в пространстве |
позволяет решать ряд простейших задач. Рассмотрим три из них. |
|
1 Нахождение координат вектора, заданного координатами начала и |
конца. |
|
|
|
где M1 (x1 , y1 , z1 )R , M 2 (x2 , y2 , z2 )R и |
x, y, z - |
Пусть вектор a = |
M1M 2 |
, |
координаты вектора. Так как |
|
= |
|
− |
|
, |
то координаты |
вектора |
M1M 2 |
OM2 |
OM1 |
находятся по формулам |
|
|
|
|
|
|
|
|
|
|
x = x2 − x1, y = y2 − y1, z = z2 − z1. |
|
|
|
|
|
|
|
(8.1) |
2 Задача о нахождении координат точки. |
|
|
|
Даны точка M 0 |
(x0 , y0 , z0 )R и вектор a{а1 ,а2 ,а3 }R . Найдем координаты |

точки M (x, y, z)R , если a = M 0 M . |
|
Легко показать, что в этом случае |
|
x = x0 + а1 , y = y0 + а2 , z = z0 + а3 . |
(8.2) |
3 Задача на деление отрезка в заданном отношении.
Точка M , принадлежащая прямой M1M 2 , делит отрезок M1M 2 в отношении λ (λ ≠ −1) (рисунок 73), если выполняется векторное равенство:
M1M = λMM2 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 73 |
|
|
|
|
|
|
Если λ > 0 , то |
|
|
|
↑↑ |
|
|
|
|
|
и говорят, что точка M делит отрезок M1M 2 |
M1M |
MM2 |
внутренним образом в отношении λ . |
|
|
|
|
|
|
|
|
|
Если λ < 0 , то |
|
↑↓ |
|
|
|
и точка M лежит вне отрезка M1M 2 , но на |
M1M |
MM2 |
прямой M1M 2 , |
тогда говорят, |
что |
|
точка M делит отрезок |
M1M 2 внешним |
образом в отношении λ . |
|
|
|
|
|
|
|
|
|
|
репера R (O; e1 , e2 , е3 ) |
|
даны |
точки |
Пусть |
относительно аффинного |
|
M1 (x1 , y1 , z1 )R , |
M 2 (x2 , |
y2 , z2 )R . Найдем координаты точки M , |
которая делит |
отрезок M1M 2 в отношении λ . Обозначим M (x, y, z)R , тогда формулы для |
нахождения координат точки, делящей отрезок в отношении λ имеют вид |
x = |
x1 + λx2 |
; y = |
y1 + λy2 |
; z = |
z1 + λz2 |
|
|
|
|
|
|
|
(8.3) |
|
|
|
|
|
1 + λ |
1 + λ |
|
|
|
|
|
|
|
|
|
|
1 + λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
частности, при λ =1 |
(то |
есть |
точка M - середина |
отрезка |
M1M 2 ), |
имеем: |
|
|
|
|
x |
+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
+ y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
= |
|
1 |
|
|
- формулы для нахождения координат середины отрезка. |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z + z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Совокупность точки O и ортонормированного базиса {i |
; |
|
|
|
|
}называется |
|
|
, k |
j |
прямоугольной декартовой системой координат в пространстве (или ортонормированным репером). Обозначается R (O; i , j, k ) (рисунок 74).
Рисунок 74
Очевидно, что прямоугольная декартова система координат является частным случаем аффинной системы координат, поэтому рассмотренные выше определения и простейшие задачи справедливы и в прямоугольной декартовой системе координат.
Нахождение расстояния между двумя точками.
Пусть |
|
|
относительно |
|
R (O; |
|
|
|
|
|
) |
заданы |
точки |
|
|
|
|
|
, |
|
, k |
|
|
|
i |
j |
M1 (x1 , y1 , z1 )R , |
|
M 2 (x2 , |
y2 , z2 )R . Найдем расстояние от точки M1 до точки M 2 . |
ρ(M |
1 |
; M |
2 |
)= |
(x |
2 |
− x )2 + (y |
2 |
− y )2 + (z |
2 |
|
− z )2 . |
|
(8.4) |
|
|
|
|
1 |
1 |
|
|
1 |
|
|
|
|
8.2 Уравнение поверхности и линии в пространстве
Поверхностью в пространстве называется геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О есть геометрическое место всех точек пространства, находящихся от точки О на расстоянии R.
Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х,у,z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.
Уравнением данной поверхности в прямоугольной системе координат Оyz называется такое уравнение F(x, y, z) = 0 , которому удовлетворяют
координаты каждой точки лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х,у,z в уравнении поверхности называются текущими координатами точек поверхности.
Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M1 (x1, y1, z1 ) на данной поверхности достаточно подставить
координаты точки M1 в уравнение поверхности вместо переменных: если эти
координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.
192
Уравнение сферы |
|
|
|
|
|
|
Найдем уравнение сферы радиуса R с центром в точке О(x0 , y0 , z0 ) . |
Согласно определению сферы расстояние любой ее точки |
M (x, y, z) от центра |
О1 (x0 , y0 , z0 ) равно радиусу R, т. е. О1M = R . Но |
О1M = |
|
|
|
|
где |
|
|
|
O1M |
О1M = (x − x0 , y − y0 , z − z0 ) . |
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
(x − x0 )2 +( y − y0 )2 +(z − z0 )2 = R |
|
|
|
|
|
|
или |
|
|
|
|
|
|
( x − x0 )2 + ( y − y0 )2 + (z − z0 )2 = R2 . |
(8.5) |
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты |
любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.
Если центр сферы О1 совпадает с началом координат, то уравнение сферы
принимает вид
x2 + y2 + z 2 = R2 .
Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:
1 Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.
2 Дано уравнение F(x, y, z) = 0 . Исследовать форму поверхности, определяемой этим уравнением.
Уравнения линии в пространстве
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (рисунок 75) или как геометрическое место точек, общих двум поверхностям.
Рисунок 75
Если F1 (x, y, z) = 0 и F2 (x, y, z) = 0 - уравнение двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе
193
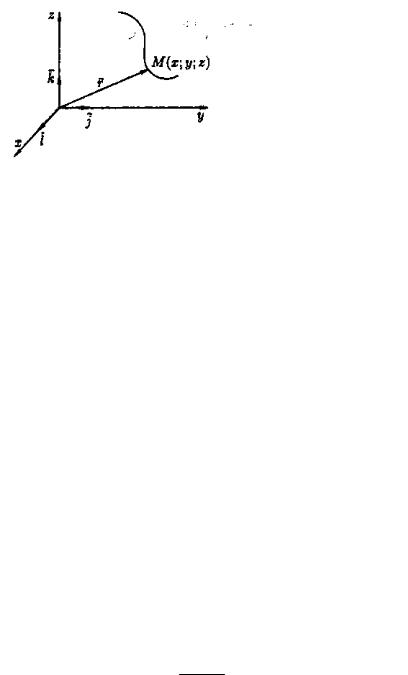
двух уравнений с тремя неизвестными: |
|
F |
(x, y, z) = 0, |
(8.6) |
1 |
|
F2 (x, y, z) = 0. |
|
Уравнения системы (8.6) называются уравнениями линий в пространстве.
y = 0,
Например, есть уравнение оси Ох.
z = 0.
Линию в пространстве можно рассматривать как траекторию движения
точки (рисунок 76). В этом случае ее задают векторным уравнением |
|
r = r (t) |
(8.7) |
|
|
|
|
|
|
Рисунок 76 |
или параметрическими уравнениями |
|
|
x = x(t), |
|
|
|
(8.8) |
y = y(t), |
|
|
|
z = z(t). |
|
|
проекций вектора (8.7) на оси координат.
8.3 Уравнения плоскости в пространстве
Простейшей поверхностью в пространстве является плоскость. Плоскость в пространстве Oxyz можно задать различными способами. Каждому из них соответствует определённый вид ее уравнения.
1 Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
Пусть в пространстве Oxyz плоскость Q задана точкой М0 (x0 , y0 , z0 ) и вектором n ={A,B,C}, перпендикулярным этой плоскости (рисунок 77).
Выведем уравнение плоскости Q. Возьмем на ней произвольную точку M (x, y, z) и составим вектор М0 M ={x − x0 , y − y0 , z − z0 }.
Рисунок 77
При любом расположении точки М на плоскости Q векторы n и М0 M взаимно перпендикулярны, поэтому их скалярное произведение равно нулю:
n М0 M = 0 , т. е. |
|
A( x − x0 ) + B( y − y0 ) +C( z − z0 ) = 0 . |
(8.9) |
Координаты любой точки плоскости Q удовлетворяют уравнению (8.9), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют.
Уравнение (8.9) называется уравнением плоскости, проходящей через данную точку М0 (x0 , y0 , z0 ) перпендикулярно вектору n ={A,B,C}. Оно первой
степени относительно текущих координат x, y, z. Вектор n ={A,B,C} называется
нормальным вектором плоскости.
Придавая коэффициентам А, В и С уравнения (8.9) различные значения, можно получить уравнение любой плоскости, проходящей через точку М0 (x0 , y0 , z0 ) . Совокупность плоскостей, проходящих через данную точку,
называется связкой плоскостей.
2 Общее уравнение плоскости |
|
Раскрыв скобки в уравнении (8.9) |
|
Ax + By +Cz + (Ax0 + By0 +Cz0 )=0 |
|
и введя обозначения |
Ax0 + By0 +Cz0 = D, получим общее уравнение |
первой |
степени с тремя переменными x, y, z : |
|
Ax + B y + C z + D = 0 . |
(8.10) |
Полагая, что по крайней мере один из коэффициентов А, В или С не равен |
нулю, например В ≠ 0 , перепишем уравнение (8.10) в виде |
|
|
D |
|
A(x − 0) + B y + |
|
+ C( z − 0) = 0. |
(8.11) |
|
|
B |
|
Сравнивая уравнение (8.11) с уравнением (8.9), видим, что уравнения (8.10), а, следовательно, и (8.11) являются уравнением плоскости с нормальным
вектором n ={A,B,C}, проходящей через точку М1 0,− DB ,0 .
Ax + By + Cz + D = 0
195

Уравнение (8.10) называется общим уравнением плоскости.
Частные случаи общего уравнения плоскости:
1 Если D = 0, то оно принимает вид Ax + B y + C z = 0 . Этому уравнению
удовлетворяет точка О(0, 0, 0), Следовательно, в том случае плоскость проходит через начало координат.
2 Если C = 0 , то имеем уравнение Ax + B y + D = 0 . Нормальный вектор n = (A, B,0) перпендикулярен оси Oz. Следовательно, плоскость параллельна оси Oz; если B = 0 -параллельна оси Оу, A = 0 — параллельна оси Ох.
3 Если C = D = 0, то плоскость проходит через О(0, 0, 0) параллельно оси Oz, т. е. плоскость Ax + B y = 0 проходит через ось Oz. Аналогично, уравнениям
B y + C z = 0 и Ax + C z = 0 отвечают плоскости, проходящие соответственно
через оси Ох и Оу. |
|
|
|
4 |
Если |
A = B = 0, то уравнение (8.10) |
принимает вид C z + D = 0 , т. е. |
z = − |
D |
. |
Плоскость параллельна |
плоскости |
Оху. |
Аналогично, уравнениям |
|
|
C |
|
|
|
|
|
Ax + D = 0 и |
B y + D = 0 отвечают |
плоскости, соответственно параллельные |
плоскостям Oyz и Оxz. |
|
|
|
5 |
Если |
A = B = D = 0 , то уравнение (8.10) примет вид C z = 0, т. е, z = 0 . |
Это уравнение плоскости Оху. Аналогично: y = 0 - |
уравнение плоскости Oxz; |
x = 0 — уравнение плоскости Оуz. |
|
|
|
3 Уравнение плоскости, проходящей через три данные точки
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M1 (x1 , y1, z1 ), M 2 (x2 , y2 , z2 ), М3 (x3 , y3 , z3 ) , не лежащие на одной
прямой. |
|
|
|
|
Возьмем на плоскости произвольную точку M (x, y, z) и составим векторы |
|
|
|
|
={x − x1 , y − y1 , z − z1}, |
|
={x2 − x1 , y2 − y1 ,z2 − z1} |
|
|
|
М1M |
М1M 2 |
|
|
={x3 − x1 , y3 − y1 , z3 − z1}. |
|
|
М1M 3 |
|
|
Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем
М1M М1М2 М1М3 = 0,
т.е.
x − x1 |
y − y1 |
z − z1 |
|
|
|
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0. |
(8.12) |
x3 − x1 |
y3 − y1 |
z3 − z1 |
|
|
Уравнение (8.12) есть уравнение плоскости, проходящей через три
данные точки.
Например, составим уравнение плоскости, проходящей через три точки
M1 (1,−4,9), M 2 (− 2,−5,7), М3 (3,−6,8) .
Подставив координаты точек M1 , M 2 и M 3 в формулу (8.12) получаем:
|
x −1 |
y + 4 z − 9 |
|
|
|
|
x −1 y +4 z −9 |
|
|
|
|
|
|
|
|
|
|
|
− 2 −1 − 5 + 4 |
7 − 9 |
|
= 0, |
|
−3 |
−1 |
−2 |
|
= 0, |
|
|
3 −1 − 6 + 4 |
8 − 9 |
|
|
|
|
2 |
−2 |
−1 |
|
|
|
|
(x −1) −1 |
−2 −( y + 4) |
−3 −2 +(z −9) |
−3 −1 |
= 0 |
, |
|
−2 |
−1 |
|
|
|
2 −1 |
|
2 −2 |
|
|
3x + 7 y −8z + 97 = 0
- уравнение искомой плоскости.
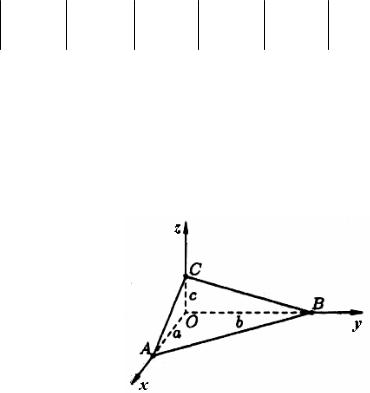
4 Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях Ох, Оу и 0z соответственно отрезки а, b и с, т. е. проходит через три точки А(а,0,0), В(0,b,0) и С(0,0,с) (рисунок 78).
|
|
|
|
|
|
|
|
Рисунок 78 |
|
Подставляя координаты этих точек в уравнение (8.12), получаем |
|
|
x − a |
y |
z |
|
|
|
|
|
|
|
|
|
− a |
b |
0 |
|
= 0. |
|
|
|
− a |
0 |
c |
|
|
|
|
Раскрыв |
определитель, имеем |
bcx − abc + abz + acy = 0 , |
т. е. |
bcx + acy + abz = abc или |
|
|
|
x |
+ |
y |
+ |
z |
=1. |
|
(8.13) |
|
a |
b |
c |
|
|
|
|
|
|
|
|
|
Уравнение (8.13) называется уравнением плоскости в отрезках на осях.
5 Нормальное уравнение плоскости
Положение плоскости Q вполне определяется заданием единичного вектора е , имеющего направление перпендикуляра ОК, опущенного на плоскость

из начала координат, и длиной р этого перпендикуляра (рисунок 79)
|
Рисунок 79 |
Пусть ОК = р, а α, β, γ |
— углы, образованные единичным вектором е с |
осями Ох, Оу, Оz. Тогда |
е ={cosα,cosβ,cosγ}. Выберем на плоскости |
произвольную точку M (x, y, z) |
и соединим ее с началом координат. Получим |
вектор r = OM ={x, y,z}.
При любом положении точки М на плоскости Q проекция радиус-вектора
r на направление вектора е всегда равна р: преr = p , т.е. r e = p или |
|
r e − p = 0. |
(8.14) |
Уравнение (8.14) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов r и e , уравнение (8.14) перепишем
в виде |
|
x cosα + y cos β + z cos γ − p = 0 . |
(8.15) |
Уравнение (8.15) называется нормальным уравнением плоскости в координатной форме.
Отметим, что общее уравнение плоскости (8.10) можно привести к нормальному уравнению (8.15) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (8.10) на нормирующий
|
множитель λ = |
1 |
, где знак берется противоположным знаку |
|
А2 + В2 + С2 |
|
± |
|
свободного члена D общего уравнения плоскости.
8.4 Плоскость. Основные задачи
1 Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
Пусть заданы две плоскости Q1 и Q2 :
Q1: A1 x + B1 y +C1 z + D1 = 0,