Unlock-Линейная алгебра Сикорская 1

Следующую формулу примем без доказательства.

Расстояние между скрещивающимися прямыми, заданными уравнениями

равно нулю. Если же они параллельны, то расстояние от прямой до плоскости есть расстояние от любой точки прямой до данной плоскости.

уравнения прямой позволяют найти координаты точки М0 (x0 , y0 , z0 ) , лежащей на ней. Поэтому расстояние между прямой L и параллельной ей плоскостью Q

равно

8.8 Уравнение цилиндрической поверхности с образующей, параллельной координатной оси. Цилиндры второго порядка

Цилиндрической поверхностью называется поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и остающейся параллельной исходному направлению (рисунок 92)

209

особенность которого состоит в том, что оно не содержит переменной z. Покажем, что если это уравнение определяет некоторую поверхность, то

она является цилиндрической поверхностью с образующей, параллельной оси Oz. Действительно, если х0 , у0 - значения переменных х и у, удовлетворяющих

уравнению (8.35), т.е. М0 (х0 , у0 , z0 ) принадлежит поверхности, определяемой уравнением, то ей будет принадлежать и точка М0 (х0 , у0 , z), так как z в

уравнении (8.35) не входит. Следовательно, поверхности целиком принадлежит прямая, проходящая через точки М0 , М , а эта прямая параллельна оси Оz. Итак,

поверхность, определяемая уравнением F ( x, y) = 0 , является цилиндрической

поверхностью с образующей, параллельной оси Оz.

Отметим, что в плоскости Оху уравнение (8.35) определяет линию (направляющую), которая в пространстве задается уже двумя уравнениями

F(x, y) = 0,

(8.36)

z = 0.

(уравнения (8.36) задают эту линию как пересечение цилиндрической поверхности (8.35) и координатной плоскости Оху).

Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является эллипс (окружность), гипербола или парабола.

К цилиндрам второго порядка относятся эллиптический цилиндр (рисунок 93), определяемый уравнением

210

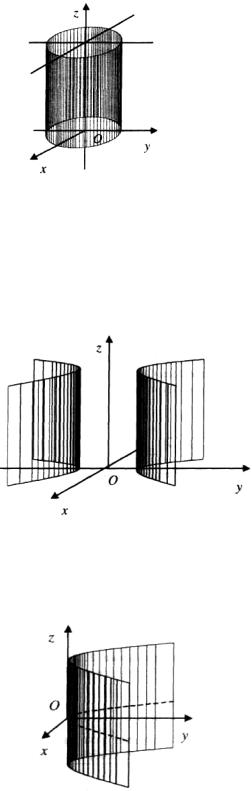
Рисунок 93

В некоторой системе декартовых прямоугольных координат; гиперболический цилиндр (рисунок 94), определяется уравнением

Замечание 1 Если уравнение

F(x, z) = 0

211

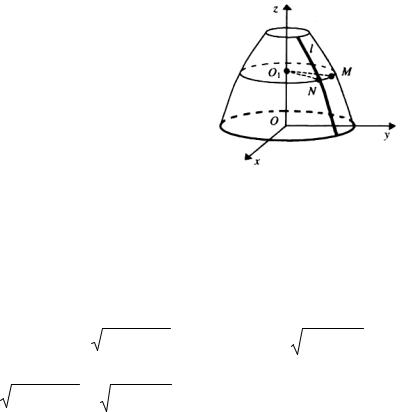
определяет некоторую поверхность, то ею является цилиндрическая поверхность с образующей, параллельной оси Оу.

Замечание 2. Если уравнение

F( y, z) = 0

определяет некоторую поверхность, то ею является цилиндрическая поверхность с образующей, параллельной оси Ох.

8.9 Уравнение поверхности вращения

Рассмотрим поверхность, полученную вращением линии l, вокруг оси Оz заданной уравнениями

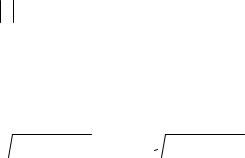
Пусть М – произвольная точка этой поверхности, X, Y, Z - ее текущие координаты. Через точку М проведем плоскость, перпендикулярную оси Оz; эта плоскость (ее уравнение z=Z) пересечет поверхность по некоторой окружности с центром в точке О1 (0,0, z) на оси Оz (рисунок 96).

Рисунок 96

Обозначим буквой N точку пересечения указанной окружности и линии l, а буквами х, у, z – ее координаты.

Поскольку длины отрезков О1М и О1N равны между собой (как радиусы одной и той же окружности), т.е. ρ(O1, M ) = ρ(O1, N) и

вращением линии (8.42) вокруг оси Oz.

Если обозначить текущие координаты точки поверхности буквами х, у, z уравнение (8.44) можно переписать так:

212

где f (z) ≥ 0 , то оно определяет поверхность вращения, так как в сечении ее плоскостью z = h будет окружность

8.10 Поверхности второго порядка

Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.

Геометрическое исследование поверхностей второго порядка проведем по заданным уравнениям с помощью метода параллельных сечений.

Уравнение (8.49) называется каноническим уравнением эллипсоида.

Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Оху. Каждая из таких плоскостей определяется уравнением вида z = h , где h — любое число, а линия, которая получается в сечении, определяется двумя уравнениями

Исследуем систему уравнений (8.45) при различных значениях h .

мнимый эллипс, т.е. точек пересечения плоскости z = h с данным эллипсоидом не существует.

0; +с) и (0; 0; — с) (плоскости z = ±c касаются эллипсоида).

3)Если h < c , то уравнения (8.49) можно представить в виде

Откуда следует, что плоскость z = h пересекает эллипсоид по эллипсу с полуосями a* = a 1 − h2 / c 2 , b* = b 1 − h2 / c 2 .

213

При уменьшении h значения а* и b* увеличиваются и достигают своих

наибольших значений при h = 0 , т.е. в сечении эллипсоида координатной плоскостью Оху получается самый большой эллипс с полуосями а*=а и b*=b.

Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz.

Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рисунок 97). Величины а, b, с называются полуосями эллипсоида. В случае а=b=с эллипсоид является сферой.

Рисунок 97

2 Однополостный гиперболоид

Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

Уравнение (8.50) называется каноническим уравнением однополостного гиперболоида.

Установим вид поверхности (8.50). Для этого рассмотрим сечения ее координатными плоскостями Oxz (у =0) и Oyz (х=0). Получаем соответственно уравнения

из которых следует, что в сечениях получаются гиперболы.

Теперь рассмотрим сечения данного гиперболоида плоскостями z = h , параллельными координатной плоскости Оху. Линия, получающаяся в сечении, определяется уравнениями

полуосями a* = a 1 + h2 / c2 , b* = b 1 + h2 / c2 , достигающими своих наименьших

значений при h = 0 , т. е. в сечении данного гиперболоида координатной плоскостью Оху получается самый маленький эллипс с полуосями а*=а и b*=b. При бесконечном возрастании h величины a* и b* возрастают бесконечно.

214

Taким образом, рассмотренные сечения позволяют изобразить однополостный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Оху (рисунок

98).

Рисунок 98

Величины a, b, c называются полуосями однополостного гиперболоида, первые две из них изображены на рисунке 98, а чтобы изобразить на чертеже полуось с, следует построить основной прямоугольник какой-нибудь из гипербол.

3 Двуполостный гиперболоид

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

Уравнение (8.52) называется каноническим уравнением двуполостного гиперболоида.

Установим геометрический вид поверхности (8.52). Для этого рассмотрим ее сечения координатными плоскостями Оxz и Oyz. Получаем соответственно уравнения

из которых следует, что в сечениях получаются гиперболы.

Теперь рассмотрим сечения данного гиперболоида плоскостями z = h , параллельными координатной плоскости Oxу. Линия, получающаяся в сечении, определяется уравнениями

215

из которых следует, что при h > c (c > 0) плоскость z = h пересекает

При h = ±c уравнениям (8.53) удовлетворяют координаты только двух точек: (0; 0; -с) и (0; 0; +с) (плоскости z = ±c касаются данной поверхности).

При h < c | уравнения (8.53) определяют мнимый эллипс, т.е. точек

пересечения плоскости z = h с данным гиперболоидом не существует.

Таким образом, рассмотренные сечения позволяют изобразить двуполостный гиперболоид как поверхность, состоящую из двух отдельных «полостей» (отсюда название двуполостный), каждая из которых имеет вид бесконечной выпуклой чаши (рисунок 99).

Рисунок 99

Величины а, b, с называются полуосями двуполостного гиперболоида. На рисунок 99 изображена величина с. Чтобы изобразить на чертеже а и b, нужно построить основные прямоугольники гипербол в плоскостях Oxz и Оуz.

4 Эллиптический параболоид

Эллиптический параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

где p > 0, q > 0.

Уравнение (8.54) называется каноническим уравнением эллиптического параболоида.

Исследуем с помощью сечений эту поверхность. Рассмотрим сначала сечения данной поверхности координатными плоскостями Oxz и Oyz. Получаем соответственно уравнения

216

из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат. Теперь рассмотрим сечения данного параболоида плоскостями z = h , параллельными координатной плоскости Оху. Линия, получающаяся в сечении, определяется уравнениями

величины а* и b* также увеличиваются; при h = 0 эллипс вырождается в точку (плоскость z = 0 касается данного параболоида). При h < 0 уравнения (8.55) определяют мнимый эллипс, т. е. точек пересечения плоскости z = h с данным параболоидом не существует.

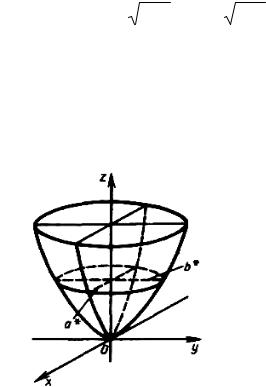
Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечной выпуклой чаши (рисунок 100).

Рисунок 100

Точка (0, 0, 0) называется вершиной эллиптического параболоида; числа

ри q – его параметрами.

Вслучае p=q уравнения (8.55) определяют окружность с центром на оси Оz, т. е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг ее оси. Такая поверхность называется

параболоидом вращения.

5 Гиперболический параболоид

Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

217

где p > 0, q > 0.

Уравнение (8.56) называется каноническим уравнением гиперболического параболоида.

Установим геометрический вид поверхности (8.56). Рассмотрим сечение параболоида координатной плоскостью Oxz ( у = 0) . Получаем уравнения

из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси 0z, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Охz ( у = h) , получаются

также направленные вверх параболы

из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Оz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x = h) , получим уравнения

из которых следует, что при h > 0 в сечении получаются гиперболы, пересекающие плоскость Охz; при h < 0 — гиперболы, пересекающие плоскость Оуz; при h = 0 гипербола вырождается в пару пересекающихся прямых

218