
Unlock-Линейная алгебра Сикорская 1
.pdf
Векторы αi′, i =1, 2, ...,n − r , линейно независимы, так как d ≠ 0 . Однако
система ( n − r )-мерных векторов
α1′, α2′ , ..., αn′−r , β′
линейно зависима, так как в ней число векторов больше их размерности. Существуют, следовательно, такие числа k1, k2 , ..., kn −r ,что
β′ = k1α1′ + k2α2′ + ... + kn −rαn′−r . |
(5.16) |
Рассмотрим теперь n -мерный вектор δ = k1α1 + k1α2 + ... + kn −rαn −r − β . Вектор δ , являясь линейной комбинацией решений системы однородных
уравнений (5.13), сам будет решением этой системы. Из (5.16) следует, что в решении δ значения для всех свободных неизвестных равны нулю. Однако то единственное решение системы уравнений (5.13), которое получается при равных нулю значениях для свободных неизвестных, будет нулевым решением. Таким образом, δ = 0 , т. е. β = k1α1 + k2α2 + ... + kn −rαn −r . Теорема доказана.
Заметим, что приведенное выше доказательство позволяет утверждать, что мы получим все фундаментальные системы решений системы однородных уравнений (5.13), беря в качестве d всевозможные отличные от нуля определители порядка n − r .
Например, пусть дана система линейных однородных уравнений
3x1 + x2 − 8x3 + 2x4 + x5 = 0, |
||||||||||||||
2x |
− |
2x |
2 |
− |
3x |
− |
7x |
4 |
+ |
2x |
= 0, |
|||
|
1 |
|
|
|
3 |
|
|
|
5 |
|
||||
|
x |
+ |
11x |
2 |
− |
12x |
+ |
34x |
4 |
− 5x |
= 0, |
|||
|
1 |
|
|
|
|
3 |
|
|
|
|
5 |
|
||
|
x |
− |
5x |
2 |
+ |
2x |
− |
16x |
4 |
+ |
3x |
= 0. |
||
|
1 |
|
|
|
|
3 |
|
|
|
5 |
|
|||
Решение. Ранг матрицы из коэффициентов равен двум, число неизвестных равно пяти, поэтому всякая фундаментальная система решений этой системы уравнений состоит из трех решений. Решим систему, ограничиваясь первыми двумя линейно независимыми уравнениями и считая x3 , x4 , x5 свободными
неизвестными. Мы получим общее решение в виде
x1 =198 x3 + 83 x4 − 12 x5 , x2 = 78 x3 − 258 x4 + 12 x5 .
Берем, далее, следующие три линейно независимых трехмерных вектора (1, 0, 0) , (0, 1, 0) , (0, 0, 1) . Подставляя компоненты каждого из них в общее
решение в качестве значений для свободных неизвестных и вычисляя значения для x1 и x2 мы получим следующую фундаментальную систему решений
заданной системы уравнений:
α1 |
19 |
, |
7 |
|
3 |
, − |
25 |
|
|
− |
1 |
, |
1 |
|
= |
8 |
, 1, 0, 0 , α2 |
= |
8 |
, 0, 1, 0 , α3 |
= |
2 |
2 |
, 0, 0, 1 . |
|||||
|
8 |
|
|
8 |
|
|
|
|
|
|
В заключении этого параграфа рассмотрим связь, существующую между решениями неоднородных и однородных систем.
Пусть дана система линейных неоднородных уравнений:
129
a x |
+ a x |
2 |
+... + a |
|
x |
n |
= b , |
||||
11 1 |
12 |
|
1n |
|
1 |
||||||
a21x1 + a22 x2 +... + a2n xn = b2 , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
........................................ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
+ a |
s2 |
x |
2 |
+... + a |
sn |
x |
n |
= b . |
|
|
s1 1 |
|
|
|
|
|
s |
||||
и система линейных однородных уравнений:
a x |
+ a x |
2 |
+ ... + a |
|
x |
n |
= 0, |
||||
11 1 |
12 |
|
1n |
|
|
||||||
a21x1 + a22 x2 + ... + a2n xn = 0, |
|||||||||||
........................................ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
x + a |
s2 |
x |
2 |
+ ... + a |
sn |
x |
n |
= 0, |
||
|
s1 1 |
|
|
|
|
|
|
||||
(5.17)
(5.18)
полученная из системы (5.17) заменой свободных членов нулями. Система (5.18) называется приведенной системой для системы (5.17). Между решениями систем (5.17) и (5.18) существует тесная связь:
Теорема 5.5 Сумма любого решения системы (5.17) с любым решением приведенной системы (5.18) снова будет решением системы (5.17).
Доказательство. Пусть с1, с2 , ..., cn - решение системы (5.17), d1, d2 , ..., dn
- решение системы (5.18). Берем любое из уравнений системы (5.17), например k - е, и вставляем в него вместо неизвестных числа c1 + d1, c2 + d2 , ..., cn + dn . Мы
n |
n |
n |
получим: ∑akj (c j + d j ) = ∑akj c j + ∑akj d j = bk + 0 = bk , |
||
j =1 |
j =1 |
j =1 |
что и доказывает теорему.
Теорема 5.6 Разность любых двух решений системы (5.17) служит решением для приведенной системы (5.18).
Доказательство. Пусть с1, c2 , ..., cn и с1′, c2′ , ..., cn′ - решения системы (5.17).
Берем любое из уравнений системы (5.18), например k -е, и подставляем в него вместо неизвестных числа c1 − c1′, c2 − c2′ , ..., cn − cn′ . Мы получим:
n |
n |
n |
∑akj ( c j − c′j ) = ∑akj c j − ∑akj c′j = bk − bk = 0 . |
||
j =1 |
j =1 |
j =1 |
Из этих теорем вытекает, что, найдя одно решение системы линейных уравнений (5.17) и складывая его с каждым из решений приведенной системы (5.18), мы получим все решения системы (5.17).
5.8 Вопросы для самоконтроля
1 Дайте определение системы линейных уравнений.
2Какая матрица называется матрицей (расширенной матрицей) системы линейных уравнений?
3Дайте определение однородной (неоднородной) системы линейных уравнений.
4Что называется решением системы линейных уравнений?
5Что означает решить систему линейных уравнений?
6Что значит система совместна, несовместна, определена, неопределена?
130
7 В чем заключается разница между общим и частным решениями системы линейных уравнений?
8 Какие две системы называются эквивалентными?
9 Какие пять преобразований системы приводят ее в эквивалентную?
10 Перечислите преобразования матрицы, преобразующие ее в эквивалентную.
11 В чем заключается суть метода Гаусса?
12 В каком случае при решении системы методом Гаусса мы можем заключить – система совместна и определена или система совместна и неопределенна?
13Теорема Крамера, ее формулировка и доказательство.
14Если система n линейных уравнений с n неизвестными не имеет решений, то что вы можете утверждать об определителе матрицы системы?
15Назовите необходимое условие наличия нетривиального решения системы линейных однородных уравнений.
16В чем заключается суть решения системы линейных уравнений матричным способом?
17Сформулируйте и докажите теорему Кронекера-Капелли.
18Сформулируйте и докажите теорему о единственности решения системы линейных уравнений.
19Если система линейных уравнений имеет единственное решение, то чему равен ранг матрицы системы?
20Что можно сказать о ранге матрицы системы линейных уравнений, если множество решений системы бесконечно?
21Какие неизвестные совместной системы называются базисными (свободными)?
22В чем заключается суть метода решения неопределенной системы?
23При каком значении ранга матрицы система линейных однородных уравнений имеет единственное нулевое решение (не только нулевое решение)?
24Если определитель системы линейных однородных уравнений равен нулю, то что вы можете сказать о количестве решений этой системы?
25В каком случае одним из решений системы линейных однородных
уравнений будет решение M1 , − M 2 ,..., (−1)n−1 M n и каким при этом будет всякое
другое решение?
26 Является ли линейная комбинация решений однородной системы линейных уравнений также решением этой системы? (тот же вопрос в случае неоднородной системы).
27 Дайте определение фундаментальной системы решений.
28 Сформулируйте теорему о зависимости числа решений системы линейных однородных уравнений и ранга матрицы системы. Докажите эту теорему.
29Что значит «приведенная система»?
30Какова связь между решениями неоднородных и однородных систем линейных уравнений?
131
Глава 6 Векторная алгебра
6.1 Векторы. Основные понятия. Линейные операции над векторами
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура.
Другие величины, например, сила, скорость, ускорение определяются не только своим числовым значением, но и направлением. Например, при движении тела следует указать не только скорость, с которой движется тело, но и направление движения. Точно так же, изучая действие какой-либо силы, необходимо указать не только значение этой силы, но и направление ее действия. Такие величины называются векторными.
Вектор это направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если А - начало вектора, а В - его конец, то
вектор обозначается символом АВ или а.
Вектор ВА (у него начало в точке В, а конец в точке А) называется противоположным вектору АВ. Вектор противоположный вектору а, обозначается −а.
Длиной или модулем вектора АВ называется длина отрезка АВи обозначается АВ .
Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 0 . Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным вектором и обозначается е . Единичный вектор, направление которого совпадает с
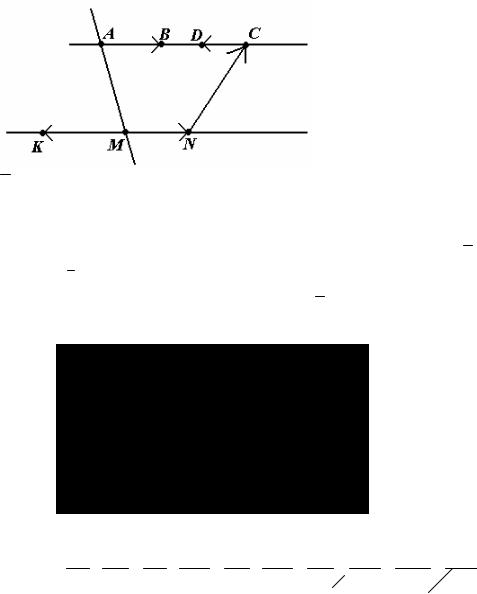
направлением вектора а, называется ортом вектора а и обозначается a0 . Векторы а и b называются коллинеарными, если они лежат на одной
прямой или на параллельных прямых: обозначают а
 b .
b .
Рисунок 17
На рисунке 17 AB|| CD , AB || MN , CD || MN , AB || NC , MN || NC .
Среди коллинеарных векторов выделяют сонаправленные и противоположнонаправленные.
132
Коллинеарные векторы называются сонаправленными, если относительно прямой, соединяющих их начала оба вектора окажутся в одной полуплоскости. В противном случае векторы называются противоположнонаправленными.
Например, векторы AB и MN - сонаправлены, так как относительно прямой (AM ) они расположены в одной полуплоскости; а векторы AB и MK относительно этой же прямой (AM ) расположены в разных полуплоскостях.
Следовательно, AB и MK - противоположнонаправлены. Знак ↑↑ используется для сонаправленных векторов; для противоположнонаправленных используется знак ↓↑.
На рисунке 17 AB ↑↑ MN , AB ↑↓ CD , AB ↑↓ MK .
Принято нуль – вектор считать коллинеарным с любым другим.
Два вектора а и b называются равными ( а=b ), если они коллинеарны,
одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку пространства.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
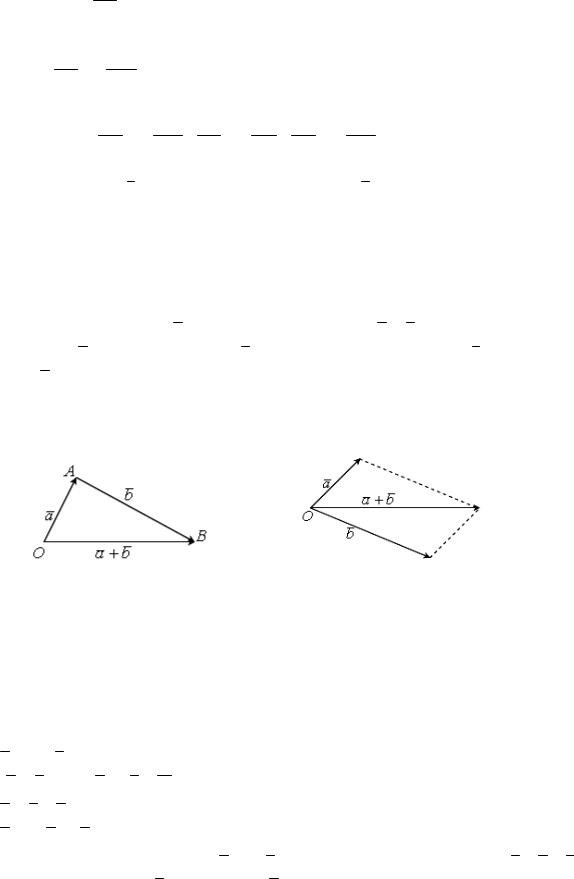
Суммой двух векторов a и b называется вектор a + b , который направлен
из начала вектора a в конец вектора b при условии, что вектор b отложен из
конца вектора a .
Для геометрического представления суммы векторов используют правила «треугольника» и «параллелограмма», проиллюстрированные на рисунках 18 и 19 соответственно.
Рисунок 18 |
Рисунок 19 |
Аналогично определяется сумма трех и более векторов. Суммой конечного числа векторов будет вектор, направленный из начала первого в конец последнего вектора, при условии, что каждый последующий вектор отложен из конца предыдущего (правило «многоугольника»).
Свойства операции сложения векторов
1)a + b = b + a (коммутативность),
2)(a + b) + c = a + (b + c) (ассоциативность),
3)a + o = a ,
4)a + (−a) = o .
Разностью двух векторов a и b называется такой вектор x = a − b , который в сумме с вектором b дает вектор a , т.е.
133
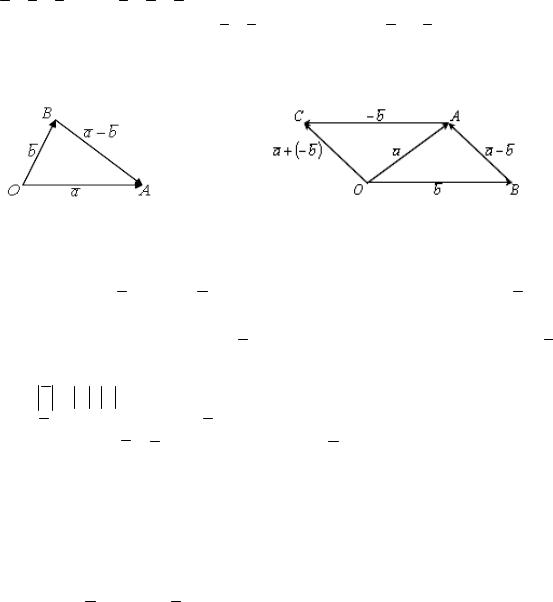
a − b = x , если b + x = a .
Чтобы построить разность a − b двух векторов a и b, нужно отложить их из одной точки и вектор разности будет направлен из конца второго вектора (вычитаемого) в конец первого вектора (уменьшаемого) (рисунок 20).
Рисунок 20 |
|
|
|
Рисунок 21 |
||
Отметим, что поскольку a − |
|
= a + (− |
|
), то разность a − |
|
равна сумме |
b |
b |
b |
||||
двух векторов a и (−b ), где (−b )- вектор, противоположный вектору b (рисунок
21).
Произведением вектора a ≠ 0 на число α ≠ 0 называется вектор b =αa ,
удовлетворяющий условиям:
1)b = α a ,
2)b ↑↑ a , если α > 0 ; b ↑↓ a , если α < 0 . Очевидно, что b = 0 , если α = 0 или a = 0 .
Из определения следует, что в результате умножения вектора на
действительное число получается вектор, коллинеарный данному, то есть αa ║a .
Свойства умножения вектора на число
1.α(βa )= (αβ )a (α, β R ),
2.1 a = a,
3.(α + β)a =αa + βa (α, β R ),
4.α(a +b )=αa +αb (α R ).
|
|
Теорема 6.1 Для любых двух коллинеарных векторов |
a |
и |
|
, где |
a ≠ |
|
|
, |
|||||||||||||||||||||||||||||||||||||||||||||||||
b |
0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
существует единственное число α такое, что |
|
|
|
|
|
|
=αa . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Доказательство. |
|
Пусть векторы |
|
a и |
|
|
|
|
|
|
|
коллинеарны. |
|
Возможны |
два |
||||||||||||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
случая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
а) Векторы a и |
|
|
|
сонаправлены ( а ↑↑ |
|
|
|
). Рассмотрим число α = |
|
|
b |
|
|
|
|
и |
|||||||||||||||||||||||||||||||||||||||||
b |
b |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сравним два вектора |
|
|
|
и αa . Имеем |
|
αa |
|
= |
|
α |
|
a |
|
= |
b |
a |
= |
|
|
|
, |
т.е. длины векторов |
|||||||||||||||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
одинаковы. Сравним |
|
направления: |
а ↑↑αa (α > 0) . |
По |
условию |
а ↑↑ |
|
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
следовательно, αа ↑↑ |
|
. |
Так как длины и направления векторов одинаковы, то |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
=αa . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
б) Векторы a |
и |
|
|
противоположно направлены ( а ↑↓ |
|
). Рассмотрим |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
b |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
134
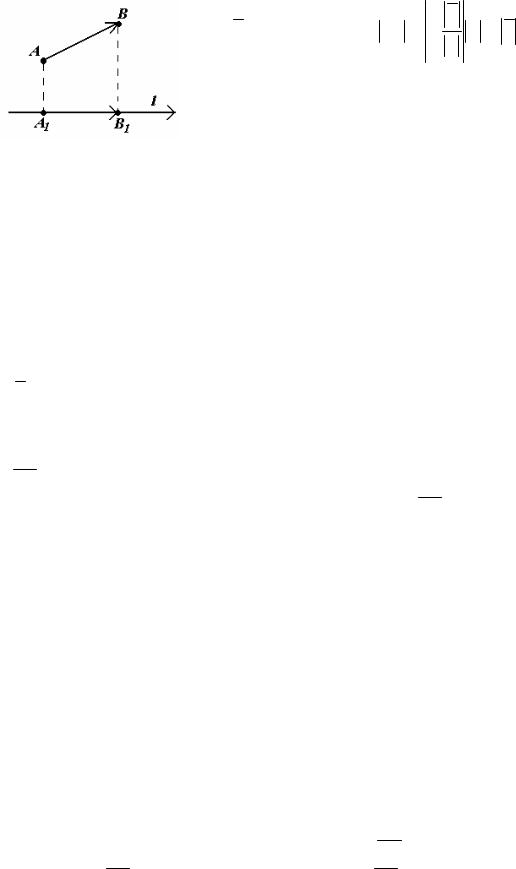
b b
число α = − a и сравним два вектора b и αa . Имеем αa = − a a = b , т.е.
длины векторов одинаковы. Сравним направления: а ↑↓αa (α < 0) . По условию
а ↑↓ |
|
, следовательно, αа ↑↓ |
|
. Так |
как |
длины и |
направления векторов |
|||||||||||||||||||||||||||||||
b |
b |
|||||||||||||||||||||||||||||||||||||
одинаковы, то и в этом случае |
|
|
|
=αa . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
b |
|
|
|
|
|
|
векторы a и |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
Пусть |
теперь |
|
|
|
=αa , тогда по |
|
определению |
|
|
либо |
||||||||||||||||||||||||
|
|
|
|
b |
|
b |
||||||||||||||||||||||||||||||||
сонаправлены, либо противоположно направлены, т.е. всегда коллинеарны. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
Докажем единственность |
существования числа |
α для коллинеарных |
||||||||||||||||||||||||||||||||
векторов a и |
|
. Предположим, |
что существуют два числа α и α1 такие, что |
|||||||||||||||||||||||||||||||||||
b |
||||||||||||||||||||||||||||||||||||||
|
|
=αa |
|
и |
|
=α1a . Тогда из условия αa =α1а |
следует, |
что числа α и α1 одного |
||||||||||||||||||||||||||||||
|
b |
b |
||||||||||||||||||||||||||||||||||||
знака, |
а из условия |
|
αa |
|
= |
|
α1а |
|
, что |
|
α |
|
= |
|
α1 |
|
. |
Значит, |
α =α1 , что противоречит |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
предложению. Число α единственное. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
Из теоремы следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
=αa |
|
- необходимое и |
достаточное условие коллинеарности двух |
|||||||||||||||||||||||||||||
|
|
|
|
b |
|
|||||||||||||||||||||||||||||||||
векторов a и b .
6.2 Проекция вектора на ось
Пусть AB - произвольный ненулевой вектор. Обозначим через A1 и B1 проекции на ось l соответственно начала A и конца B вектора AB и рассмотрим
вектор |
A1B1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проекцией вектора |
|
на ось l называется положительное число |
|
|
|
|
|
|
|
|
, |
|||||||||||
AB |
|
A1B1 |
|
|
||||||||||||||||||
если вектор |
|
|
и ось l одинаково направлены и отрицательное число − |
|
|
|
|
|
|
, |
||||||||||||
A1B1 |
|
A1B1 |
|
|
||||||||||||||||||
если вектор |
|
|
и ось l противоположно направлены (рисунок 22) |
|
|
|
|
|
|
|||||||||||||
A1B1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 22
Если точки A1 и B1 совпадают, то проекция вектора AB на ось l равна 0. Проекция вектора AB на ось l обозначается так: прl AB .
Угол ϕ между вектором a и осью l изображен на рисунке 23. Очевидно,
0 ≤ϕ ≤π .
135
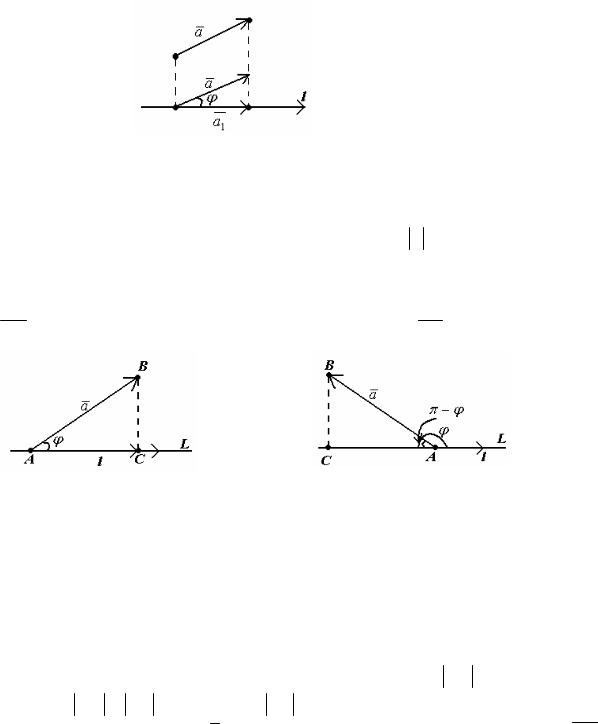
Рисунок 23
Свойства проекций
1. Проекция вектора a на осью l равна произведению модуля вектора a на косинус угла ϕ между вектором и осью, т.е. прl a = a cosϕ .
Действительно, пусть l лежит на прямой L, а его началом является точка А. Совместим начало вектора а с точкой А, и пусть его концом будет точка В (рисунок 24). Построим ортогональную проекцию С точки В на прямую L. Тогда
вектор АС является ортогональной проекцией вектора а = АВ на прямую L.
а) |
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
||
Рисунок 24 |
|
|
|
|
|
|||||||||||||
Если угол ϕ между векторами а |
|
|
|
|
|
|
острый (см. рисунок 24, |
|
а), то из |
|||||||||
и l |
|
|
|
|||||||||||||||
прямоугольного треугольника ACB имеем |
|
АС |
|
= |
|
АВ |
|
cosϕ . |
и точка С лежат |
|||||||||
|
|
|
|
|||||||||||||||
|
|
|||||||||||||||||
Если угол ϕ тупой (см. рисунок 24,б), то конец вектора l |
||||||||||||||||||
по разные стороны от точки А. Это |
значит, что векторы |
|
и |
|
|
имеют |
||||||||||||
АС |
||||||||||||||||||
l |
||||||||||||||||||
противоположные направления, а проекция вектора аравна − АС . Поэтому АС = АВсos(π −ϕ) = − АВ cosϕ .
Если угол ϕ = 900 или а = 0 , то точка С совпадает с точкой А и вектор AC
является нулевым вектором. Однако сos900 = 0 , следовательно, и в этом случае данное свойство справедливо.
2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.
прl (a1 + а2 ) = прl a1 + прl a2 .
Действительно, пусть точки A и A1 - соответственно начало и конец вектора a1 , точки A1 и A2 - начало и конец вектора a2 (рисунок 25).
136

|
|
Рисунок 25 |
|
|
|
|
Обозначим через A′, A1′, A2′ |
соответственно проекции точек A, A1 , A2 на ось |
|||||
l . По определению, прl a1 = A′A1′, |
прl a2 = A1′A2′ , прl (a1 + a2 ) = прl |
|
= A′A2′ . |
|||
AA2 |
||||||
Тогда |
справедливо |
следующее |
А′А2′ = А′А1′ + А1′А2′ . |
Отсюда |
||
прl (a1 + а2 ) = прl a1 + прl a2 .
3. При умножении вектора a на число λ его проекция на ось также умножается на это число, т.е. прl (λ a ) = λ прl a .
Доказательство этого свойства предлагаем читателю выполнить самостоятельно.
6.3 Линейная зависимость и линейная независимость векторов. Свойства линейно зависимой системы векторов
Пусть даны векторы a1, a2 ,..., an и действительные числа α1,α2 ,...,αn . Рассмотрим вектор a = α1a1 +α2a2 +... +αnan , который назовем линейной комбинацией векторов a1, a2 ,..., an ; действительные числа α1,α2 ,...,αn назовем
коэффициентами линейной комбинации.
Очевидно, что, выбирая другую совокупность чисел β1, β2 ,..., βn , получим другую линейную комбинацию тех же самых векторов: b = β1a1 + β2a2 +... + βnan .
То есть можно построить бесчисленное множество линейных комбинаций одной и той же системы векторов.
Система векторов a1, a2 ,..., an называется линейно зависимой, если существуют действительные числа α1,α2 ,...,αn , из которых хотя бы одно отлично от нуля, такие, что линейная комбинация векторов a1, a2 ,..., an с этими числами равна нулевому вектору, то есть:
α1a1 +α2a2 +... +αnan = |
|
|
|
|
(6.1) |
|
0 |
|
|
||||
Если |
соотношение |
(6.1) |
выполняется |
только |
при условии |
|
α1 = α2 = ... = αn = 0 , то система векторов называется линейно независимой.
Свойства линейно зависимой системы векторов
1. Если один из векторов системы нуль-вектор, то вся система векторов линейно зависима.
Действительно, пусть в системе a1 , a2 ,..., an−1 ,0 таким вектором является
137
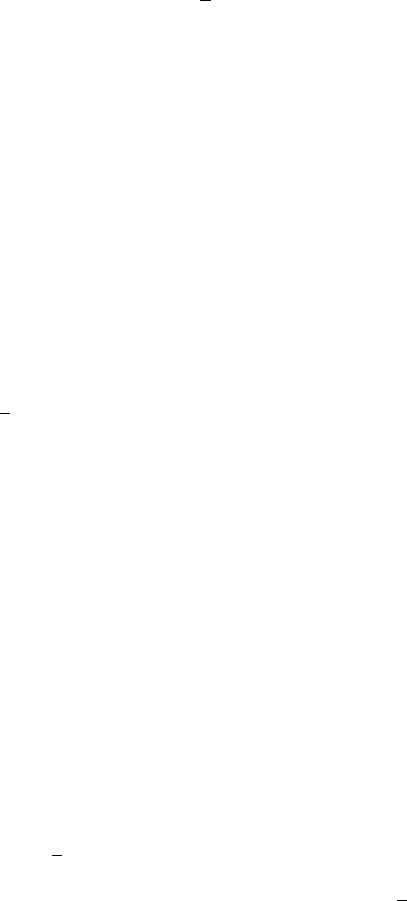
последний вектор (этого всегда можно добиться путем перенумерации векторов). Рассмотрим систему чисел 0,0,0,…,1.
Очевидно, что 0 a1 + 0 a2 + ... + 0 an−1 +1 0 = 0 , поэтому система векторов линейно зависима.
2. Если один из векторов системы является линейной комбинацией остальных векторов, то вся система векторов линейно зависима (справедливо и обратное утверждение).
Доказательство. Необходимость. Предположим, что векторы a1, a2 ,..., an линейно зависимы. Согласно определению линейной зависимости векторов, в равенстве α1a1 +α2a2 +... +αnan = 0 слева есть хотя бы один ненулевой коэффициент, например α1. Оставив первое слагаемое в левой части равенства,
перенесем остальные слагаемые в правую часть, при этом меняем у них знаки. Разделив полученное равенство на α1, получим
а |
= − |
α2 |
a |
|
−... − |
αn |
a |
n |
, |
α1 |
|
|
|||||||
1 |
|
|
2 |
|
α1 |
|
|||
т.е. представили вектор а1 в виде линейной комбинации векторов a2 ,..., an . |
|||||||||
Достаточность. Пусть, например, первый вектор а1 можно представить в
виде линейной комбинации остальных векторов: a1 = β2 a2 + ... + βn an .
Перенесем все слагаемые из правой части в левую, тогда получим
a1 − β2 a2 − ... − βn an = 0 ,
т.е. линейную комбинацию векторов a1, a2 ,..., an с коэффициентами a1 =1,α2 = −β2 ,...αn = −βn , равную нулевому вектору. В этой комбинации не все
коэффициенты равны нулю. Согласно определению линейной зависимости векторов, векторы a1, a2 ,..., an линейно зависимы. Что и требовалось доказать.
3. Если часть системы векторов линейно зависима, то вся система
векторов линейно зависима. |
например, α1a1 + α2a2 + ...+ αsas = |
|
и α1 ≠ 0 , то |
||
Действительно, если, |
0 |
||||
будет выполнено равенство |
|
|
|
|
|
α1a1 +α2a2 +... +αs as |
+ 0as +1 + 0as +2 +... + 0an = |
|
, |
||
0 |
|||||
причем α1 ≠ 0 . |
|
|
|
|
|
4.Система векторов, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
Предлагаем свойства 4 читателю доказать самостоятельно.
5.Система векторов, состоящая из двух векторов, линейно зависима тогда и только тогда, когда эти векторы коллинеарны.
Действительно, если векторы а и b линейно зависимы, то один из них, например, а, выражается через другой, т.е. а = λb , где λ -действительное число.
Согласно определению произведения вектора на число, векторы а и b являются коллинеарными.
Пусть теперь векторы а и b коллинеарны. Если они оба нулевые, то очевидно, что они линейно зависимы, так как любая их линейная комбинация
равна нулевому вектору. Предположим, что один из этих векторов не равен 0 ,
138
