Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4603 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Московский государственный университет приборостроения и информатики
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Unlock-Линейная алгебра Сикорская 1

.pdf
Скачиваний:
48
Добавлен:
09.04.2015
Размер:
5.18 Mб
Скачать
☆

Q2 : A2 x + B2 y +C2 z + D2 = 0 .

Под углом между плоскостями Q1 и Q2 понимается один из двугранных

углов, образованных этими плоскостями.

На основании рисунка 80 заключаем, что угол ϕ между нормальными векторами n1 ={A1 ,B1 ,C1} и n2 = {A2 ,B2 ,C2} плоскостей Q1 и Q2 равен одному из этих углов.

Рисунок 80

Поэтому cosϕ = n1 n2 или n1 n2

cosϕ =

A1 A2

+ B1B2

+ C1C2

.

(8.16)

A2 + B2 + C 2 A2 + B2 + C 2

 

 

 

Для нахождения острого угла следует взять модуль правой части.

Рисунок 81

Если плоскости Q1 и Q2 перпендикулярны (рисунок 81, а), то их нормальные векторы тоже перпендикулярны, т. е. n1 n2 (и наоборот). Но тогда

n1 n2 = 0 , т. е. A1A2 + B1B2 +C1C2 =0 . Полученное равенство есть условие перпендикулярности двух плоскостей Q1 и Q2 .

Если плоскости Q1 и Q2 параллельны (рисунок 81. б), то будут

коллинеарны и их нормальные векторы n1, n2

(и наоборот). Из условия

коллинеарности векторов получаем, что

 

 

А1

=

В1

=

С1

.

(8.17)

 

А

В

С

2

2

2

 

 

 

 

Это и есть условие параллельности плоскостей Q1 и Q2 .

199

2 Расстояние от точки до плоскости

Рассмотрим в пространстве некоторую плоскость Q и произвольную точкуМ0 (x0 , y0 , z0 ) . Выберем для плоскости единичный нормальный вектор n с

началом в некоторой точке М1(x1, y1, z1) Q , и пусть

ρ(М0 ,Q) - расстояние от

точки М0 до плоскости Q . Тогда (рисунок 82)

 

ρ(М0 ,Q) =

прn

 

 

=

n

 

 

,

(8.18)

M1M 0

M1M 0

так как

 

n

 

=1.

 

 

 

 

Рисунок 82

Если плоскость Q задана в прямоугольной системе координат своим

уравнением Ax + B y + C z + D = 0 , то ее нормальным вектором является вектор с координатами {A, B,C} и в качестве единичного нормального вектора можно выбрать

n =

 

{A, B,C} .

 

 

 

 

 

 

 

 

 

 

 

 

 

A2 + B2 + C 2

 

 

 

 

 

 

 

 

 

 

 

Так как точка M1 Q , то можно найти координаты вектора

 

:

 

M1M 0

 

 

 

= {x0 − x1 , y0 − y1 , z0 − z1}.

 

 

 

 

 

 

 

 

 

M1M 0

 

 

 

 

 

 

 

 

Записывая

скалярное

 

произведение

n

 

 

в координатной форме

и

 

M1M 0

преобразуя (8.18), получаем

 

 

 

 

 

 

 

 

 

 

 

 

ρ(М0

,Q) = A(x0 − x1) + B( y0 − y1) + C(z0 − z1) =

 

 

 

 

 

 

 

 

 

 

 

A2 + B2 + C 2

 

 

 

 

 

 

 

 

= Ax0 + By0 + Cz0 − ( Ax1 + By1 + Cz1)

=

 

 

 

 

 

 

 

 

 

 

 

 

A2 + B2 + C 2

 

 

 

 

 

 

 

 

 

=

Ax0

+ By0 + Cz0 + D

,

 

 

 

 

 

 

 

 

 

 

A2 + B2 + C 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

поскольку Ax1 + By1 + Cz1 = −D .

 

 

 

Q

задана

уравнением

Отметим,

что

если

плоскость

x cosα + y cos β + z cos γ − p = 0 , то

расстояние

от

точки М0 (x0 , y0 , z0 )

до

плоскости Q может быть найдено по формуле d = x cosα + y cos β + z cos γ − p .

200

8.5 Уравнения прямой в пространстве

1 Векторное уравнение прямой

Положение прямой в пространстве вполне определено, если задать какую-

либо точку М0 на прямой и вектор s , параллельный этой прямой. Вектор s

называется направляющим вектором прямой. Пусть прямая L задана точкой

М0 (x0 , y0 , z0 )

и направляющим вектором s ={m,n, p}. Возьмем на прямой L

произвольную

точку М(x, y, z) . Обозначим радиус-векторы

точек М и М0

соответственно через

r

и

r0 . Очевидно, что три вектора

r

 

r0

и

 

связаны

,

M 0 M

соотношением

 

 

 

 

 

 

 

 

 

 

 

=

r0 +

 

 

 

 

 

 

 

 

 

(8.19)

r

M 0 M

 

 

 

 

 

 

 

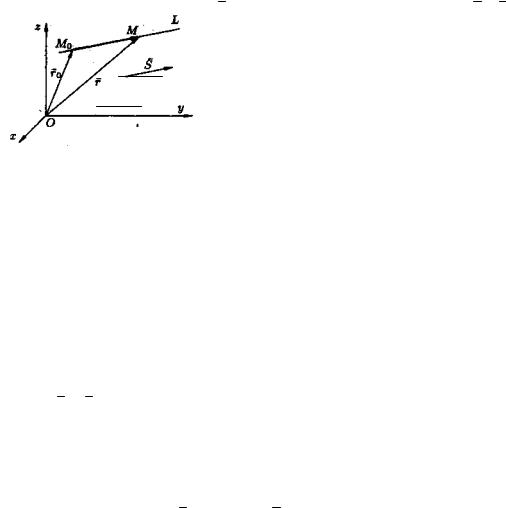
Вектор M 0 M , лежащий на прямой L, параллелен направляющему вектору

s , поэтому M 0 M = ts , где t — скалярный множитель, называемый параметром,

может принимать различные значения в зависимости от положения точки М на прямой (рисунок 83)

 

 

 

 

 

 

 

 

Рисунок 83

 

Уравнение (8.19) можно записать в виде

 

r

=

r0 +ts

(8.20)

Полученное уравнение называется векторным уравнением прямой.

2 Параметрические уравнения прямой

 

Замечая, что

r

={x, y, z},

r0 ={x0 , y0 , z0 },ts ={tm,tn,tp}

уравнение (8.20)

можно записать в виде

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xi

+ yj + zk = (x0 + tm)i + ( y0 + tn) j + (z0 + tp)k

 

Отсюда следуют равенства:

 

x = x0 +mt,

 

y = y0 +nt,

(8.21)

z = z0 + pt.

 

есть (8.21) napaметрические уравнения прямой в пространстве.

201

 

 

3 Канонические уравнения прямой

 

 

 

 

Пусть

 

 

={m,n, p} — направляющий вектор прямой L и

М0 (x0 , y0 , z0 )

 

s

точка, лежащая на этой прямой. Вектор

 

, соединяющий точку М0 с

M 0 M

произвольной точкой М(x, y, z)

прямой L, параллелен вектору s . А значит, эти

векторы

 

 

 

коллинеарны.

Поэтому

координаты

вектора

 

 

={x − x0 , y − y0 , z − z0 } и вектора s ={m,n, p} пропорциональны:

 

М0 M

 

 

 

x − x0

=

y − y0

=

z − z0

.

 

 

 

(8.22)

 

 

 

m

n

 

 

 

 

 

 

 

 

 

 

 

p

 

 

 

 

Уравнения (8.22) называются каноническими уравнениями прямой в пространстве.

Замечания: 1) Уравнения (8.22) можно было бы получить сразу из параметрических уравнении прямой (8.21), исключив параметр t. Из уравнений

(8.21) находим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x − x0

=

y − y0

=

z − z0

= t.

 

 

 

 

 

 

 

 

 

 

 

 

 

m

n

p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2) Обращение в нуль одного из знаменателей уравнений (8.22) означает

обращение в нуль соответствующего числителя.

 

 

 

 

 

 

Например, уравнения

 

x

−1

=

y

+1

=

z −

3

задают прямую, проходящую

 

 

2

 

0

 

4

 

 

через точку М0 (1,−1,3) перпендикулярно оси Оу (проекция вектора s

на ось Oу

равна нулю). Но это означает, что прямая лежит в плоскости

у = −1,

и поэтому

для всех точек прямой будет у +1 = 0 .

 

 

 

 

 

 

 

 

 

 

 

 

4 Уравнение прямой в пространстве, проходящей через две точки

 

 

Пусть прямая L проходит через точки

s

M1 (x1 , y1 , z1 ),

M 2 (x2 ,

y2 , z2 ). В

качестве

направляющего

 

 

вектора

 

можно

взять

вектор

 

 

={x2 − x1 , y2 − y1 , z2 − z1}, т.е. s =

 

 

(рисунок 84).

 

 

 

М1M 2

М1М2

 

 

 

 

Рисунок 84

Следовательно,

m = x2 − x1

, n = y2 − y1, p = z2 − z1 . Поскольку прямая

проходит через точку

M1 (x1, y1, z1 ), то, согласно уравнениям (8.22), уравнения

прямой L имеют вид

202

x − x1

=

y − y1

=

z − z1

.

(8.23)

 

 

 

x

2

− x

 

y

2

− y

 

z

2

− z

 

 

1

 

 

1

 

 

1

 

 

Уравнения (8.23) называются уравнениями прямой, проходящей через две данные точки.

5 Общие уравнения прямой

Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей. Рассмотрим систему уравнений

 

A x + B y + C z + D = 0,

 

 

(8.24)

 

1

1

1

1

 

 

A2 x + B2 y + C2 z + D2 = 0.

 

 

 

Каждое из уравнений этой системы определяет плоскость. Если плоскости

не параллельны

(координаты векторов n1 ={A1 ,B1 ,C1

}

и

n2 ={A2 ,B2 ,C2 } не

пропорциональны), то система (8.24) определяет прямую L как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы (рисунок 85).

Рисунок 85

Уравнения (8.24), т.е.

A1 x + B1 y + C1 z + D1 = 0,A2 x + B2 y + C2 z + D2 = 0.

называют общими ypaвнениями прямой.От общих уравнений (8.24) можно перейти к каноническим уравнениям (8.22). Координаты точки М0 (x0 , y0 , z0 ) на

прямой L получаем из системы уравнений (8.24), придав одной из координат произвольное значение (например, z = 0 ).

Так как прямая L перпендикулярна векторам n1, n2 , то за направляющий

вектор s прямой L можно принять векторное произведение [n1, n2

]:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

s = [n1 , n2 ]=

i

 

 

j

 

 

A1

B1

C1

.

 

 

A2

B2

C2

 

 

Замечание: Канонические уравнения прямой легко получить, взяв две какие-либо точки на ней и применив уравнения (8.23).

203

8.6 Прямая линия в пространстве. Основные задачи

1 Угол между прямыми. Условия параллельности и перпендикулярности прямых.

Пусть прямые L1 и L2 заданы уравнениями

 

L

:

x − x1

 

=

y − y1

 

=

z − z1

,

 

 

 

 

 

 

 

 

 

 

 

1

 

 

m1

 

 

n1

 

 

 

p1

 

 

 

 

 

 

 

 

 

 

 

 

L

:

x − x2

=

y − y2

 

=

z − z2

.

 

 

 

 

 

 

 

 

2

 

 

m2

 

 

n2

 

 

 

p2

 

 

 

 

 

 

 

 

 

 

 

 

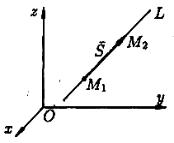
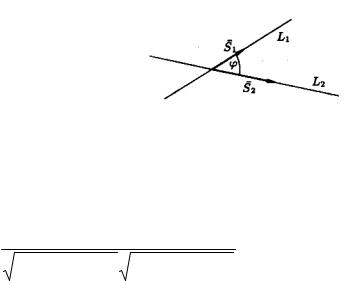
Под углом между этими прямыми понимают угол между

направляющими векторами s1 ={m1 ,n1 , p1

} и s2 ={m2 ,n2 , p2

}(рисунок 86).

Рисунок 86

Поэтому, по известной формуле для косинуса угла между векторами, получаем

cosϕ =

s1 s2

 

или

 

 

 

s

 

s

2

 

 

 

 

 

 

 

1

 

 

 

 

cosϕ =

m1m2 +n1n2 + p1 p2

.

(8.25)

+n2

+ p2

m2 +n2

m2

+ p2

 

1

1

1

2

2

2

 

Для нахождения острого угла между прямыми L1 и L2 числитель правой

части формулы (8.25) следует взять по модулю.

 

Если прямые L1 и L2

перпендикулярны, то в этом и только в этом случае

имеем cosϕ = 0 .

Следовательно,

числитель дроби (8.25) равен

нулю, т. е.

m1m2 + n1n2 + p1 p2 = 0 - условие перпендикулярности прямой.

Если прямые L1 и L2 параллельны, то параллельны их направляющие векторы s1 и s2 . Следовательно, координаты этих векторов пропорциональны, т.е.

 

m1

=

n1

=

p1

 

- условие параллельности прямых.

 

 

 

m

2

n

p

 

 

 

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

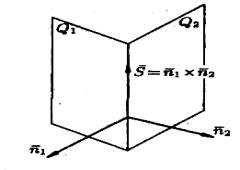
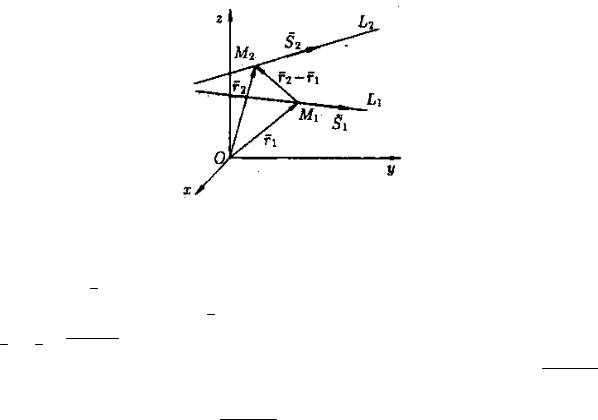
2 Условие, при котором две прямые лежат в одной плоскости.

 

 

 

 

Пусть прямые L1 и L2 заданы каноническими уравнениями

 

 

 

 

 

x − x1

 

=

y − y1

=

z − z1

и

x − x2

=

y − y2

=

z − z2

 

 

 

 

 

 

 

n

p

 

 

 

 

 

 

 

 

 

m

 

 

 

 

m

2

 

n

2

 

p

2

 

 

 

 

 

 

 

1

 

1

1

 

 

 

 

 

 

 

204

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Их направляющие векторы соответственно

s1 ={m1 ,n1 , p1} и

s2 ={m2 ,n2 , p2 }(рисунок 87).

 

Рисунок 87

Прямая L1 проходит через точку M1 (x1, y1, z1 ) , радиус-вектор которой обозначим через r1 ; прямая L2 проходит через точку M 2 (x2 , y2 , z2 ) , радиусвектор которой обозначим через r2 . Тогда

r2 − r1 = M1M 2 ={x2 − x1 , y2 − y1 , z2 − z1}.

Прямые L1 и L2 лежат в одной плоскости, если векторы s1 , s2 , M1M 2 компланарны. Условием компланарности векторов является равенство нулю их смешанного произведения: s1 s2 M1M 2 = 0, т.е.

 

x2 − x1

y2 − y1 z2 − z1

 

 

 

 

 

 

m1

n1

p1

 

= 0.

 

m2

n2

p2

 

условия прямые L1 и L2 лежат в одной

При выполнении

этого

плоскости, то есть либо пересекаются, если s2 ≠ λs1 , либо параллельны, если s2 = λs1.

8.7 Прямая и плоскость в пространстве. Основные задачи

1 Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости

Пусть

плоскость Q задана уравнением Ax + B y + C z + D = 0 , прямая L

уравнениями

x − x0

=

y − y0

=

z − z0

.

m

n

 

 

 

 

p

Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Обозначим через ϕ - угол между плоскостью Q и прямой L, а через θ -угол, между векторами n ={A,B,C},s ={m,n, p} (рисунок 88).

205

 

 

 

 

 

 

 

 

Рисунок 88

 

 

Тогда cosθ =

 

 

n

s

 

. Найдем синус угла ϕ , считая ϕ ≤

π

:

 

 

n

 

s

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

π

 

 

 

 

 

 

= cosθ . Так как sin ϕ ≥ 0 , получаем

 

 

sin ϕ = sin

−θ

 

 

2

 

 

 

 

 

 

 

 

 

 

sinϕ =

Am + Bn + Cp

 

A2 + B2 + C 2 m2 + n2 + p2 .

(8.26)

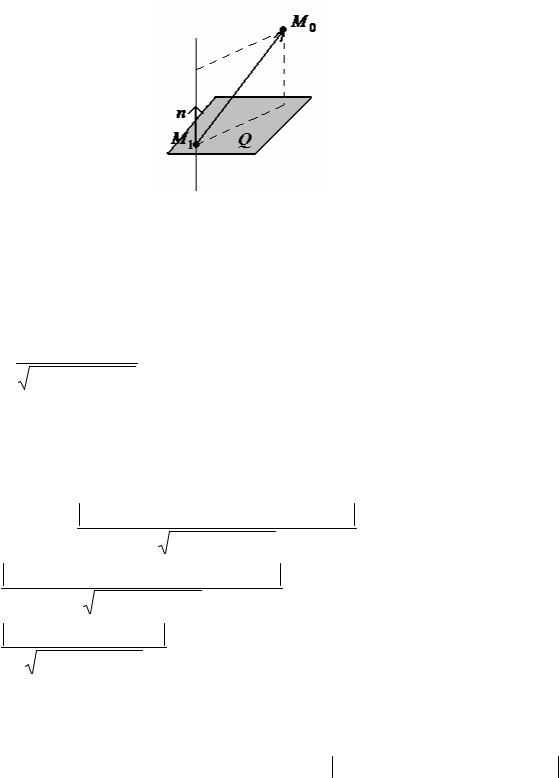
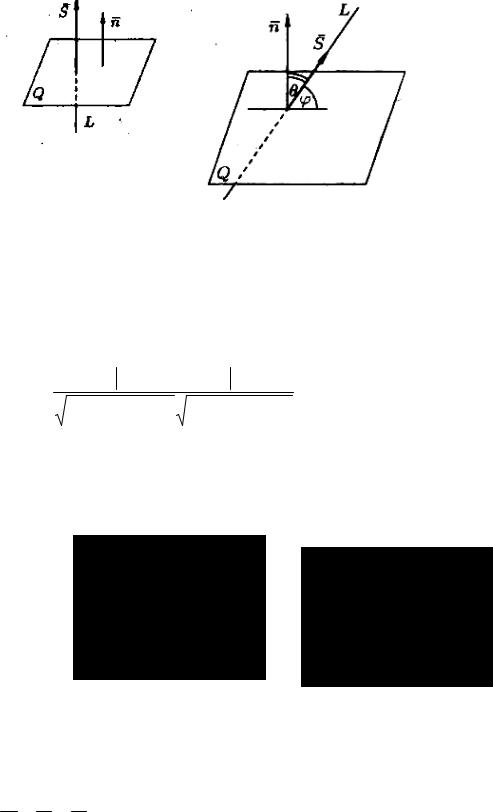
Если прямая L параллельна плоскости Q, то векторы n, s перпендикулярны (рисунок 89), а потому n s = 0 , т. е.

Am + Bn +Cp = 0

является условием параллельности прямой и плоскости.

Рисунок 89 Рисунок 90

Если прямая L перпендикулярна плоскости Q, то векторы n, s

параллельны (рисунок 90). Поэтому равенства mA = Bn = Cp

являются условиями перпендикулярности прямой и плоскости.

206

2 Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости

Для того, чтобы найти точку пересечения прямой

 

 

x − x0

 

=

y − y0

=

z − z0

 

(8.27)

 

m

n

p

 

 

 

 

с плоскостью

 

 

 

 

 

 

 

Ax + B y + C z + D = 0 ,

(8.28)

надо решить систему уравнений (8.27) и (8.28). Проще всего это сделать, записав уравнения прямой (8.27) в параметрическом виде:

x = x0 +mt,

 

 

= y0

+nt,

 

y

 

 

= z0

+ pt.

 

z

 

Подставляя выражения для x, y, z в уравнение плоскости (8.28), получаем

уравнение A(x0 +mt) + B( y0 +nt) +C(z0 + pt) + D = 0 или

 

t(Am + Bn + Cp) + (Ax0 + By0 + Cz0 + D) = 0 .

(8.29)

Если прямая L не параллельна плоскости, т. е. если Am + Bn + Cp ≠ 0 , то из

равенства (8.29) находим значение t:

t = − Ax0 + By0 + Cz0 + D . Am + Bn + Cp

Подставляя найденное значение t в параметрические уравнения прямой, находим координаты точки пересечения прямой с плоскостью.

Рассмотрим теперь случай, когда прямая L параллельна плоскости Q, т.е.

если Am + Bn +Cp = 0 :

а) если F = Ax0 + By0 + Cz0 + D ≠ 0 , то прямая L параллельна плоскости

и пересекать ее не будет (уравнение (8.29) решения не имеет, так как имеет вид

0 t + F = 0, F ≠ 0 );

б) если Ax0 + By0 + Cz0 + D = 0 , то уравнение (8.29) имеет вид

0 t + 0 = 0 ; ему удовлетворяет любое значение t, любая точка прямой является точкой пересечения прямой и плоскости. Заключаем: прямая лежит в плоскости. Таким образом, одновременное выполнение равенств

Am + Bn + Cp = 0,

Ax0 + By0 + Cz0 + D = 0.

является условием принадлежности прямой плоскости.

3 Расстояние от точки до прямой

Расстояние от точки М1 (x1, y1, z1 ) до прямой L, заданной каноническими

уравнениями

x − x0

=

y − y0

=

z − z0

, может быть вычислено при помощи

m

n

p

 

 

 

 

207

векторного произведения. Из канонического уравнения прямой можем найти точку М0 (x0 , y0 , z0 ) принадлежащую этой прямой и ее направляющий вектор

s ={m,n, p}. Построим параллелограмм на векторах s и M 0 M1 . Тогда расстояние от точки M1 до прямой L будет равно высоте h параллелограмма (рисунок 91).

 

 

 

 

 

 

 

 

 

Рисунок 91

 

Значит, расстояние вычисляется по формуле

 

 

 

 

 

[

 

 

 

, s]

 

 

 

 

 

 

 

 

 

ρ(М1

, L) =

M 0M1

(8.30)

 

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

 

 

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где числитель представляет собой площадь этого параллелограмма. Используя формулы вычисления длины вектора и векторного произведения векторов через их координаты, получаем

 

y − y

0

z −z

2

x − x

z −z

0

2

x − x

0

y − y

2

 

1

1

0 +

1

0 1

+

1

1

0

ρ(М1, L) =

n

 

p

 

m

p

 

 

m

 

n

(8.31)

 

 

 

 

m2 +n2 + p2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

- формула расстояния от точки до прямой.

4 Расстояние между прямыми

Если прямые пересекаются, то очевидно, что расстояние между ними равно нулю. Поэтому о расстоянии имеет смысл говорить если прямые параллельны или скрещиваются. Чтобы найти расстояние между параллельными прямыми, достаточно вычислить расстояние от произвольной точки, например, второй прямой до первой прямой, т.е. можно воспользоваться формулой (8.31)

Пусть две прямые заданы каноническими уравнениями

L :

x − x1

=

y − y1

=

z − z1

, L

2

:

x − x2

=

y − y2

=

z − z2

.

 

 

 

 

 

 

1

m1

 

n1

 

p1

 

m2

 

n2

 

p2

 

 

 

 

 

 

 

Таким образом расстояние между ними вычисляется по формуле

208

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности