Unlock-Линейная алгебра Сикорская 1

Член 2aij xi x j можно записать, таким образом, в виде

2aij xi x j = aij xi x j + a ji x j xi ,

а всю квадратичную форму f - в виде суммы всевозможных членов aij xi x j , где i и j уже независимо друг от друга принимают значения от 1 до n . Таким образом,

иназовем ее матрицей квадратичной формы (12.5).

Всилу условия (12.4) матрица A - симметрическая (ее элементы, симметричные относительно главной диагонали, равны между собой).

Очевидно, квадратичной форме (12.5) n переменных x1, x2 , ..., xn

соответствует единственная симметрическая матрица (12.6).

Обратно, всякой симметрической матрице (12.6) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Например, составим матрицу квадратичной формы

Решение. Чтобы составить матрицу A, нужно данную квадратичную форму записать в виде (12.1). Для этого смешанные члены – 3x1x2 , 4x1x3 , − 8x2 x3

представим в виде суммы двух равных слагаемых:

−1,5x1x2 −1,5x2 x1 , 2x1x3 + 2x3 x1 , − 4x2 x3 − 4x3 x2 .

Таким образом, заданной квадратичной форме соответствует

Рангом квадратичной формы называется ранг ее матрицы. Квадратичная форма n переменных называется невырожденной, если ее матрица – невырожденная, т.е. r = n , и вырожденной, если r < n .

Квадратичную форму (12.5) n переменных x1, x2 , ..., xn можно записать в матричном виде. Действительно, если X - матрица-столбец из переменных

289

представляет собой матричный вид квадратичной формы (12.5).

12.2 Преобразование квадратичной формы линейным однородным оператором

290

этом случае говорят, что квадратичная форма f (x1, x2 , ..., xn ) переводится в квадратичную форму ϕ(y1, y2 , ..., yn ) линейным однородным оператором (12.8).

Линейный однородный оператор (12.9) называется невырожденным, если det B ≠ 0 .

Две квадратичные формы называются конгруэнтными, если существует

переводится в себя тождественным оператором (невырожденным). Второе свойство следует из того, что произведение двух невырожденных линейных однородных операторов являются невырожденным оператором.

где C = BT AB .

Поскольку

CT = (BT AB)T = (BT (AB))T = (AB)T (BT )T = (BT AT )B = BT AB = C ,

т. е. CT = C , то C - симметрическая матрица. Следовательно, C = BT AB является матрицей квадратичной формы ϕ(y1, y2 , ..., yn ).

Следствие 1 Определители матриц конгруэнтных невырожденных действительных квадратичных форм имеют одинаковые знаки.

Действительно, поскольку матрицы A и C двух конгруэнтных

квадратичных форм связаны соотношением C = BT AB , где B - невырожденная матрица, то

det C = det(BT AB)= det BT det A det B = (det B)2 det A ,

или

det C = (det B)2 det A.

Следовательно, det C det A > 0 , т.к. (det B)2 > 0 .

Следствие 2 Конгруэнтные квадратичные формы имеют одинаковые

ранги.

291

Действительно, поскольку ранг матрицы не меняется при умножении ее слева или справа на невырожденную матрицу и C = BT AB , то rangC = rangA .

Рассмотрим теперь, по аналогии с указанной в начале параграфа геометрической задачей приведения уравнения центральной кривой второго порядка к каноническому виду (12.3), вопрос о приведении произвольной квадратичной формы некоторым невырожденным линейным оператором к виду суммы квадратов неизвестных, т.е. к такому виду, когда все коэффициенты при произведениях различных неизвестных равны нулю. Мы уже знаем этот специальный вид квадратичной формы называется каноническим.

Предположим сначала, что квадратичная форма f от n неизвестных x1, x2 , ..., xn уже приведена невырожденным линейным оператором к каноническому виду

могут, конечно, быть нулями. Докажем, что число отличных от нуля коэффициентов в (12.11) равно рангу r формы f .

В самом деле, так как мы пришли к (12.11) при помощи невырожденного оператора, то квадратичная форма, стоящая в правой части равенства (12.11), также должна быть ранга r . Однако матрица этой квадратичной формы имеет диагональный вид

И требование, чтобы эта матрица имела ранг r , равносильно предположению, что на ее главной диагонали стоит ровно r отличных от нуля элементов.

Основная теорема о квадратичных формах

Теорема 12.2 Любая квадратичная форма некоторым невырожденным линейным оператором может быть приведена к каноническому виду.

Доказательство проведем индукцией по числу переменных. При n =1 теорема верна, так как в этом случае квадратичная форма f (x1 )= a11x12 имеет

канонический вид. Докажем теорему для квадратичных форм от n переменных, считая ее уже доказанной для форм с меньшим числом переменных. Предположим, что среди коэффициентов aii (i =1, 2, ..., n) данной квадратичной

формы

n n

f (x1, x2 , ..., xn )= ∑∑aij xi x j

i =1 j =1

292

по предположению ее можно привести к каноническому виду. Следовательно, квадратичная форма f также приведена к каноническому виду (12.13). Отметим,

что линейный оператор (12.12) является невырожденным, так как его определитель равен a11 ≠ 0 . Оператор, обратный оператору (12.12), также будет

невырожденным, он приводит исходную форму f к виду (12.13).

Случай, когда все коэффициенты aii = 0 (i =1, 2, ..., n) , но, например, a12 ≠ 0 , с помощью оператора

x1 = z1 − z2 , x2 = z1 + z2 , xi = zi (i = 3, 4, ..., n)

сводится к предыдущему. Действительно, этот оператор является невырожденным, ибо его определитель отличен от нуля:

невырожденных операторов, которые можно заменить одним невырожденным оператором – их произведением, приводится к каноническому виду.

Доказательство основной теоремы закончено. Метод, использованный в этом доказательстве, может быть применен в конкретных примерах для

293

приведения квадратичной формы к каноническому виду. Нужно лишь вместо индукции, которую мы использовали в доказательстве, последовательно выделять

Ввиду отсутствия в этой форме квадратов неизвестных мы применим сначала невырожденный линейный оператор

x1 = y1 − y2 , x2 = y1 + y2 , x3 = y3

после чего получим:

f = 2 y12 −2 y22 −4 y1 y3 −8y2 y3 .

Теперь коэффициент при y12 отличен от нуля, и поэтому из нашей формы

можно выделить квадрат одного неизвестного. Полагая z1 = 2 y1 − 2 y3 , z2 = y2 , z3 = y3 ,

т.е. действуя линейным оператором, для которого обратный будет иметь матрицу

мы приведем f к виду

Пока выделился лишь квадрат неизвестного z1 , так как форма еще содержит произведение двух других неизвестных. Используя неравенство нулю коэффициентов при z22 , еще раз применим изложенный выше метод.

Совершая линейный оператор t1 = z1 , t2 = −2z2 − 4z3 , t3 = z3 ,

для которого обратный имеет матрицу

мы приведем, наконец, форму f к каноническому виду

294

Линейный оператор, приводящий (12.14) сразу к виду (12.16), будет иметь своей матрицей произведение

Можно подстановкой проверить, что невырожденный (так как определитель равен −1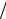2 ) линейный оператор

x1 = 12 t1 + 12 t2 + 3t3 , x2 = 12 t1 − 12 t2 − t3 ,

превращает (12.14) в (12.16).

12.3 Нормальный вид квадратичной формы

Каноническая квадратичная форма называется нормальной (или имеет нормальный вид), если αii =1 (i =1, 2, ..., r), т.е. отличные от нуля коэффициенты

ψ(z1, z2 , ..., zn )= z12 + z22 +... + zk2 − zk2+1 −... − zr2

внормальном виде. Очевидно, что число входящих сюда квадратов равно рангу

формы.

295

12.4 Закон инерции квадратичных форм

Канонический вид, к которому приводится данная квадратичная форма, не является для нее однозначно определенным, так как любая квадратичная форма может быть приведена к этому виду различными способами.

Однако, несмотря на то, что к нормальному виду квадратичная форма также может быть приведена различными преобразованиями, оказывается, нормальный вид может быть только один. Об этом свидетельствует теорема,

выражающая закон инерции квадратичных форм:

Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная действительная квадратичная форма невырожденным действительным линейным оператором, не зависит от выбора оператора.

Доказательство. Предположим, что квадратичная форма f (x1, x2 , ..., xn ) ранга r двумя способами приведена к нормальному виду

Поскольку переход от переменных x1, x2 , ..., xn к переменным y1, y2 , ..., yn

осуществлен действительным линейным невырожденным оператором, то и обратный оператор

также является действительным невырожденным. Точно так же будет действительным невырожденным и линейный оператор

уравнений однородной системы меньше числа неизвестных, система имеет

действительные числа, то все квадраты в равенстве (12.21) – неотрицательны, что влечет за собой равенство их нулю, в частности,

296

Следовательно, система n линейных уравнений zi (x)= 0(i =1, 2, ..., n) с n

неизвестными x1, x2 , ..., xn имеет ненулевое решение α1, α2 , ..., αn . Определитель

такой системы должен быть равен нулю. Это противоречит тому, что преобразование (12.19) является невырожденным. Предположение, что l < k , приводит к такому же противоречию. Отсюда следует равенство k = l , которое и доказывает теорему.

Число положительных квадратов в нормальной форме, к которой приводится данная действительная квадратичная форма, называют положительным индексом инерции этой формы, число отрицательных квадратов – отрицательным индексом инерции, разность между положительным и отрицательным индексами инерции – сигнатурой формы f .

Очевидно, если известен ранг формы, то задание любого из трех указанных выше чисел определяет два других.

Теорема 12.4 Две действительные квадратичные формы от n переменных тогда и только тогда конгруэнтны, когда они имеют одинаковые ранги и одинаковые сигнатуры.

Доказательство. Пусть форма f переводится в форму ϕ невырожденным

линейным действительным оператором. При этом, как известно, ранг не меняется. Этот оператор не меняет и сигнатуры, поскольку в противном случае формы f и

ϕприводились бы к различным нормальным видам, а тогда форма f

приводилась бы к обоим этим нормальным видам, что противоречит закону инерции квадратичных форм.

Обратно, если квадратичные формы имеют одинаковые ранги и одинаковые сигнатуры, они приводятся к одному и тому же нормальному виду и поэтому могут быть переведены одна в другую.

Если дана квадратичная форма g в каноническом виде,

с не равными нулю действительными коэффициентами, то ранг этой формы равен, очевидно, r . Легко видеть, далее, употребляя уже применявшийся выше способ приведения такой формы к нормальному виду, что положительный индекс инерции формы g равен числу положительных коэффициентов в правой части

равенства (12.24). Отсюда и из предшествующей теоремы вытекает такой результат:

Квадратичная форма f тогда и только тогда будет иметь форму (12.24) своим каноническим видом, если ранг формы f равен r , а

положительный индекс инерции этой формы совпадает с числом положительных коэффициентов в (12.24).

12.5 Знакоопределенные квадратичные формы

297

Действительная квадратичная форма f (x1, x2 , ..., xn ) называется

является положительно определенной тогда и только тогда, когда она принимает положительные значения при любой ненулевой системе значений x1, x2 , ..., xn .

Доказательство. Пусть f (x1, x2 , ..., xn ) - положительно определенная форма, т.е. преобразуется к виду (12.25) невырожденным линейным оператором

ненулевой. Действительно, в противном случае имели бы линейную однородную систему с отличным от нуля определителем, обладающую ненулевым решением, что противоречит следствию из теоремы Крамера. При подстановке ненулевой системы значений y1, y2 , ..., yn в (12.25) получим ϕ(y1, y2 , ..., yn )> 0 .

Обратно, пусть квадратичная форма f не является положительно

определенной, т.е. ее ранг или положительный индекс инерции меньше n ; линейным невырожденным оператором (12.26) эта форма приводится, в частности, к одному из видов:

ϕ(y1, y2 , ..., yn )= y12 + y22 + ... + yn2−1,

ϕ(y1, y2 , ..., yn )= y12 + y22 +... + yn2−1 − yn2 .

В этом случае существует ненулевая система значений x1, x2 , ..., xn , при

которой ϕ(x1, x2 , ..., xn )= 0 или ϕ(x1, x2 , ..., xn )< 0 ; такими значениями будут значения, полученные из системы (12.26) при y1 = 0 , y2 = 0 , …, yn −1 = 0 , yn =1.

Познакомимся с теоремой, которая позволит по коэффициентам квадратичной формы установить, будет ли эта форма положительно определенной. Предварительно введем вспомогательное понятие.

Пусть дана квадратичная форма f (x1, x2 , ..., xn ) с матрицей A = (aij ). Главными минорами квадратичной формы f называются миноры порядка 1, 2

…, n матрицы A, расположенные в левом верхнем углу; последний из них совпадает с определителем матрицы.

Итак, теорема 12.6:

298