Методика выбора алгоритмов поисковой оптимизации.

Создание эффективных пакетов программ оптимизации представляет собой большую научно - исследовательскую задачу. Сложность решения оптимизационных задач связана со следующими обстоятельствами:

1. Высокой размерностью и чрезвычайной сложностью математических моделей проектируемых объектов.

2. Трудоемкостью формализации целей и критериев проектирования.

3. Выбор эффективных методов решения оптимизационных задач.

4. Эффективность поискового метода определяется следующими показателями:

• область сходимости

• скорость сходимости

• время счета одной итерации

• объемом памяти

• классом задач решаемых методом и т.д.

Не существует единого поискового метода.

Не поиск универсальных методов, а разумное сочетание методов позволяет эффективно решать задачи. Необходимо иметь библиотеку разнообразных программ, позволяющих осуществить выбор одного, либо совокупности методов, причем задача может решатся как в диалоговом так и в пакетном режиме. Представляется целесообразным использование автоматического пакета с управляющей программой, осуществляющей автоматически выбор последовательности используемых алгоритмов. Такой пакет необходим в случаях:

1. С системой работает пользователь не являющийся специалистом в этой области.

2. Решение задачи должно протекать без участия человека.

Для решения отмеченной проблемы в пакетах диалоговой оптимизации используются блоки накапливания опытов, в которых собирается статистика по решаемым задачам, что позволяет вырабатывать рекомендации по использованию методов поиска. Для этой же цели используется эвристические оценки, идентифицирующие в процессе поиска ситуации типовыми ситуациями.

Подходы которые закладываются в пакеты программ оптимизации:

Метод ситуационного управления:

1. Поисковая идентификация. Включает два этапа:

• идентификация поисковой ситуации

• выбор метода соответствующего данной поисковой ситуации

ситуация_1(S1)-область экстремумаS1,S2…- область в которой функция качества описывается функцией своих независимых переменных:

S2- ситуация типа «седло» или «овраг»;

S3- крутой подъем, спуск;

S4- обычный подъем, спуск;

S5- площадка;

S6- многоэкстремальность;

S7- наличие либо отсутствие ограничений на область поиска;

S8- количество независимых переменных.

В ситуации S1 выгодно принимать методы: градиентный, метод Ньютона, квази Ньютоновские методы.S2: используются овражные методы (например метод тяжелого шарика).S3,S4: используются градиентный метод и метод наискорейшего спуска.S5: случайные методы,S6: случайные методы, либо глобальный поиск с равномерной плотностью распределения пробных шагов,S7: случайные методы либо могут быть использованы другие методы (градиентный, наискорейшего спуска), только предварительно учесть ограничения вQ(X) с использованием «штрафных» функций.

Ограничения:

S8: при большом числе независимых переменных используются случайные методы, при большом количестве независимых переменных можно использовать метод Зейделя и покоординатный спуск (n<10 переменных), более 10 – ти – покоординатный спуск.

Пакет программ должен содержать:

1. Библиотека выше перечисленных методов оптимизации.

2. Блок определяющий поисковую ситуацию.

3. Программа реализации вычисления Q(X).

4. Модули учитывающие ограничения на область поиска.

5. Реализованные виды критериев остановок (по ресурсу шагов, по точности).

Должны определить в какой поисковой ситуации находимся и выбрать соответствующий метод. Работа блока поисковой ситуации.

Ситуация «овраг» определяется на основе нескольких поисковых шагов, в результате выполнения которых выясняется, что приращение по одной или нескольким координатам больше, чем по остальным; число определяется либо на основе литературных данных, либо на основе накопленных пакетов программ. Аналогично оцениваются ситуации подъем спуск, крутой подъем спуск.

Динамика решения задачи с использованием данного подхода заключается в том, что блок анализа поисковой ситуации в начальной точке Х⁽⁰⁾определяет поисковую ситуацию, есть или нет ограничения; находится ли данная точка в области допустимых значений и анализируется поисковая ситуация для данной точки. Для данной поисковой ситуации выбирается из библиотеки соответствующий метод или решается задача до момента смены поисковой ситуации, анализ которой постоянно ведет блок анализа поисковой ситуации. После определенного количества шагов производится анализ: не окончен ли поиск, если нет – процедура поиска оптимального решения продолжается с выдачей необходимых пользователю данных в виде таблиц и рисунков.

При структурной адаптации ориентированной на анализ поисковой ситуации необходимо дополнительное время на проведение анализа и распознавания этой поисковой ситуации, выделения элементов рельефа оптимизируемой функции, для этого используются субъективные оценки распознавания к какому классу относится та или иная поисковая ситуация ( крутой подъем или спуск).

Другие подходы реализации структурной адаптации алгоритмов поиска заключаются в «состоятельности» указанных алгоритмов. Такой подход описывается в работах [13, 14] для однопроцессорной системы, а для многопроцессорной в работе [15].

Гибридный алгоритм – на определенном цикле работает определенный алгоритм. Решение проблемы структурной адаптации таким алгоритмом изложено в работах [16-18]. Эффективность гибридных алгоритмов, представляющих комбинацию алгоритмов существенно зависят от упорядоченного набора чисел {n₁............n_m} номер алгоритма из множества А. Еслиni– случайные числа, то имеем гибридный алгоритм со случайным набором локальных алгоритмов аi. При отсутствии глобальной информации о решаемой задаче, эффективно применение локально – оптимальных алгоритмов. Локально – оптимальным алгоритмам называется алгоритм, который заkшагов осуществил существенной продвижение в сторонуminфункции,

Если не задана априорная информация об эффективности используемых алгоритмов, эту информацию можно получить двумя способами:

1. способ накопления информации о решении тестовых задач и составление лицевого счета.

2. проверка работоспособности каждого из алгоритмов при выполнении одинакового количества итераций при решении реальной задачи, где k– число итераций, выбирается около 5.

в вышеперечисленных системах, снабженных средствами структурной адаптации последовательно решается две задачи:

- идентификация поисковой ситуации (или оценка эффективности работы алгоритма)

- выбор адекватного эффективного алгоритма

3. предложенный в работе [21] подход к оптимизации, реализуемый коллективом независимых стохастических автоматов, также может использован в решении задач выбора алгоритма оптимизации.

Система оптимизации состоит из объекта оптимизации, заданного в виде функции многих переменных, Q(x₁,…x_n), присутствует автоматный оптимизатор АО, в котором реализуетсяNавтоматов (алгоритмов). блок формирования алгоритмов: в нем заданы алгоритмы и соответствующие параметры. Каждому алгоритму ставится в соответствии вектор, компоненты которого представляют лицевые счета алгоритма. В моменты переключения с алгоритма на алгоритм эти лицевые счета позволяют установить приоритет в их использовании в зависимости от успешности предыдущей работы. блок формирования состоит из блока оценки и блока управления. Блоки оценки по значениям функции качества вырабатывается коэффициент удовлетворительности работы автоматного оптимизатора λ.

В блоке оценки значение λ вырабатывается в зависимости от величины и формируется по формуле:

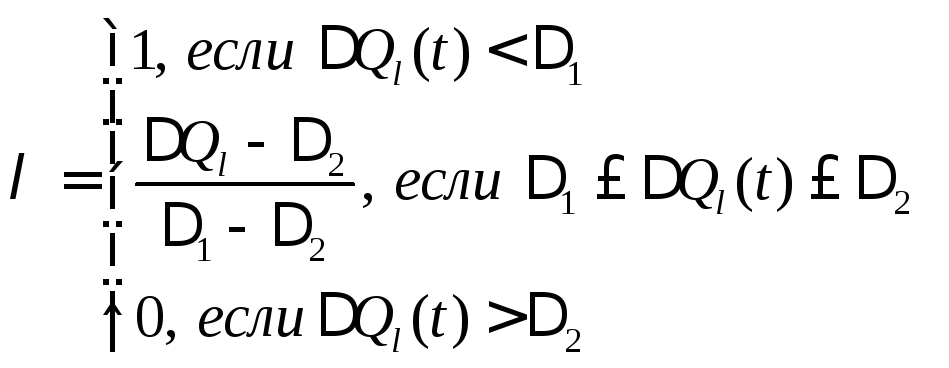
- оценка среднего значения разности между числом удачных и неудачных испытаний, отнесенных к числу lпоследних шагов, совершенных к моменту времениt.

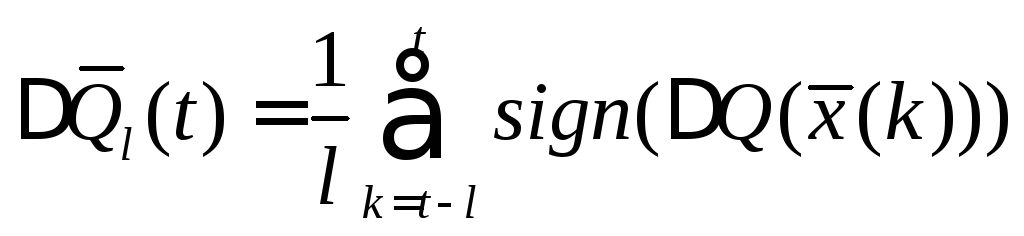
Выбор порогов иопределяется числом допустимых сбоев системы заlшагов.

При λ=1 система полностью удовлетворена работой, вычисления продолжаются с выбранным алгоритмом.

При λ=0 система неудовлетворенна работой, что приводит к смене алгоритма.

вычисление нового значения λ проходит через λ шагов, одновременно с формированием структуры автоматного оптимизатора число шагов lтоже меняется.

где - постоянные величины, соответствующие времени между переформированиями, при полном возбуждении (λ=0) и полном торможении (λ=1).

Вероятности (jменяется от 1 доN) использования алгоритмов увеличиваются, а времяlмежду переходами с алгоритма на алгоритм уменьшается.

В момент формирования счетов, которые учитывают блок формирования, каждый из алгоритмов a_jотносятся либо к числу «работающих», либо к «безработным».

Если a_j был «безработным» в момент времениt, то новое значение лицевого счета для него рассчитывается по следующим образом:

Для j-ого работающего алгоритмазначение вероятности остаться работать:

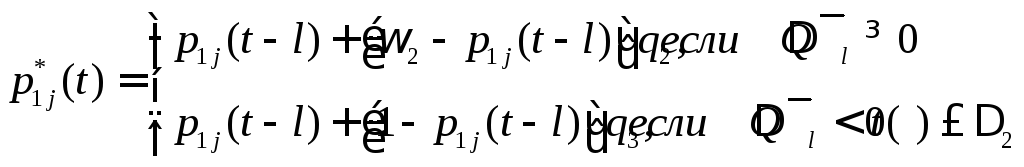
Если j- ый алгоритм «безработный», то компоненты вектора лицевого счетаp_1jубывают со скоростьюq₁стремясь к предельному значению ω₁, что приводит к увеличению компонентыp_0j(t). Для «работающего» алгоритма имеем, что если заlпредыдущих шагов система сделала больше удачных шагов, чем неудачных, то компонентывозрастают стремясь к единице со скоростьюq₃, в противном случае они убывают, стремясь к предельному значению ω₂, со скоростьюq₂.

Переключение алгоритмов происходит следующим образом: если a_jявляется «безработным», то с вероятностьюp_1jон будет относится к «работающим» , а с вероятностьюp_0jостанется «безработным».

В этой работе проведены эксперименты и выведены следующие числа:

Пределы изменения других параметров системы:

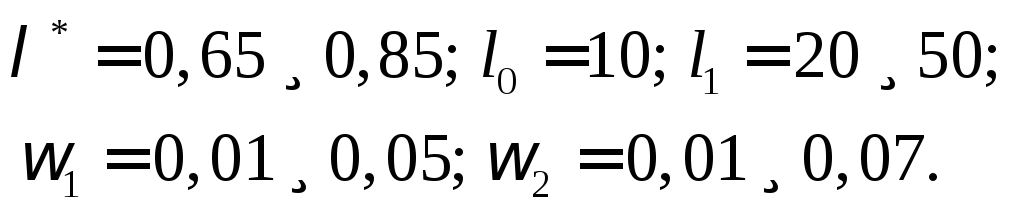
Для уменьшения времени формирования автоматной оптимизации был введен порог λ^*. Если, то следующиеlшагов структура АО считается неизменной, в противном случае осуществляется формирование структуры АО в соответствии с лицевыми счетами алгоритмов.

Постановка задачи

1. На основе теоретически – экспериментального анализа множества существующих методов структурной адаптации определить конечное их множество, пригодное для решения практических задач оптимизации.

2. Сформировать и определить критерии эффективности функции алгоритма оптимизаций в процессе поиска.

3. Разработать архитектуру системы оптимизации с использованием параметрической и структурной адаптации.

4. Реализовать программный комплекс, ориентированный на современную вычислительную технику.

Общая характеристика комплекса программ оптимизации.

Комплекс имеет модульную структуру. Составляющие комплекс блоки (содержащие один или несколько модулей) обеспечивают выполнение следующих функций:

- ввод данных и печать в виде таблиц

- расчет критериев оптимизации

- идентификации поисковой ситуации

- выбор из библиотеки в соответствии с данной поисковой ситуацией и стратегии отбора алгоритма оптимизации.

- оценка эффективности выбранного алгоритма

- проверка условий окончания поиска

- печать результатов оптимизации в виде таблицы.

Комплекс программ ориентирован на решение задач безусловной оптимизации. Решение задач условной оптимизации при помощи этого комплекса использования метода «штрафных» и барьерных» функций. Процесс решения задачи включает в себя этапы:

1. выбор алгоритма оптимизации

2. решение задачи: алгоритма с запоминанием промежуточных результатов

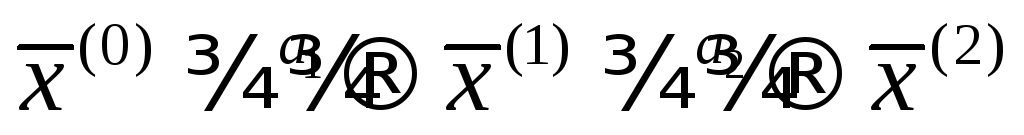
3. возврат к этапу 1, если алгоритм a_jоптимизации не найден, при этом в качестве исходной точки берется точка с наименьшим значениемQ(x) получения алгоритмаa_j. Априорно трудно указать правило выбора, которое производило бы переключение алгоритмов для более эффективного отыскания решения. Поэтому в пакет введены различные стратегии выбора методов.

а) простейший подход – случайный : выбор алгоритма случайным образом, через фиксированное число шагов не зависимо от результатов поиска. Выбор осуществляется с вероятностью:

- общее число алгоритмов к

б) адаптивный (выбор алгоритма на основе решающего правила, для каждой поисковой ситуации, анализ которого осуществляется в случае неудачного поиска предыдущим алгоритмом).

в) детерминированный (реализует работу жестко – фиксированной последовательности поисковых процедур):

- промежуточные области – используются детерминированные методы первого порядка

- в области экстремума используются методы второго порядка, либо квазиньютоновские методы

г) реализуют идею поиска оптимума коллективом независимых автоматов

д реализуют идею стратегии «здравого смысла»: непрерывная работа алгоритма, выбранного первоначально случайным образом до момента выполнения условия окончания поиска

Функционирование системы оптимизации предполагает наличие информации об эффективности алгоритмов поиска, накапливаемой на основе статистики решения оптимизационных задач, либо с помощью расчетов на тестовых функциях.

Эффективность алгоритма отражает возможность достижения с его помощью конечной цели при поиске оптимального решения.

приняты два типа характеристик эффективности алгоритма поиска:

1. локальные – вычисляемые на каждом шаге оптимизации.

2. глобальные – дающие каждому алгоритму оценку после решения задачи

Локальные характеристики – критерии, служащие для определения момента окончания поиска, либо перехода к более эффективным алгоритмам.

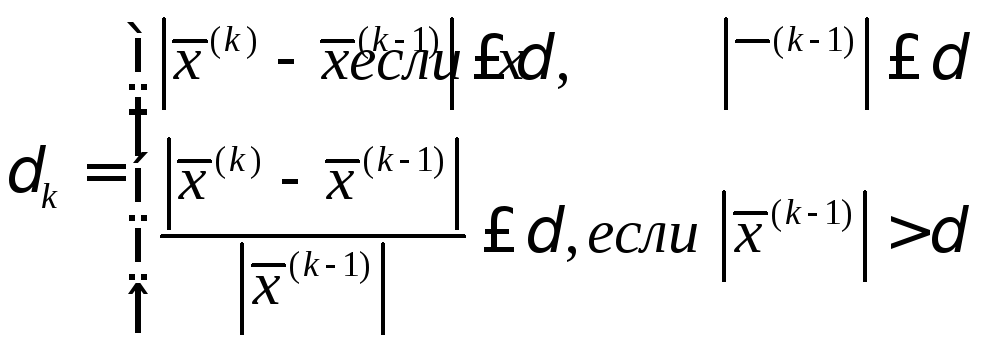
На каждом шаге вычисляются показатели эффективности, которые <1, в противном случае необходима замена на более эффективный.

Оценка эффективности может быть определена, как N₁,N₂…N_k- количество шагов, проделываемых тем или другим алгоритмом.

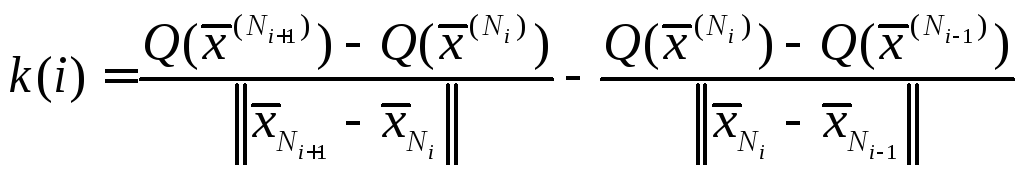
Если signk(i)<0, то удача, еслиsignk(i)≥0, то неудача.

На основе сопоставительного анализа работоспособности методов оптимизации, изложенного в литературе, произведен выбор эффективных, достаточно просто реализуемых алгоритмов, предназначенных для работы в различных ситуациях.

Методы классифицируются следующим образом:

1. методы случайного поиска, используют только значение оптимизируемой функции

2. градиентные методы, используют значение функции качества и ее первую производную

3. квазиньютоновские методы

4. овражные методы поиска

5. методы поиска глобального экстремума.

71