Методы линеаризации уравнений

Существует ряд методов линеаризации уравнений:

1. Нелинейная функция является аналитической в рабочей области и ее можно разложить в ряд Тейлора:

(9)

Сделаем линеаризацию первого уравнения из системы (9) при условии малости приращений относительно положения равновесия или номинального режима, характеризованного этим переменными :

- отклонения

y₀ ,u₀ - номинальный режим

f(y₀,u₀)=0номинальный режим

(10)

(11)

y=y₀; u=u₀

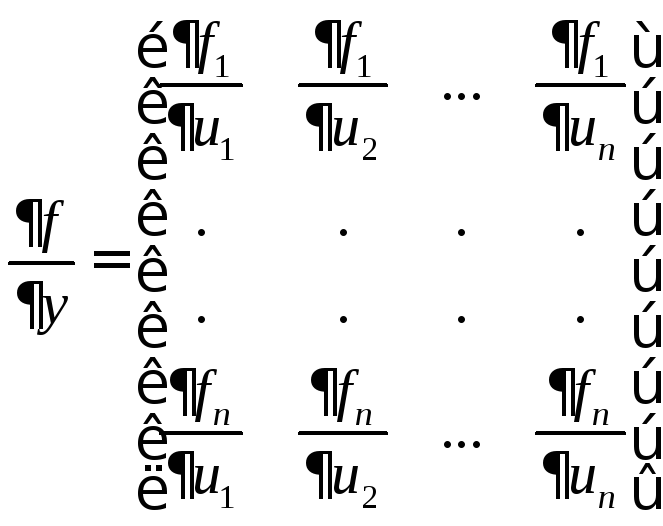
(11^’)

y=y₀; u=u₀

Аналогично и для второго уравнения системы:

(12)

Матрицы (11) и (11’) являются матрицами Якоби.

2. Предполагается, что линейные характеристики не могут быть описаны аналитически, а задаются в графической форме.

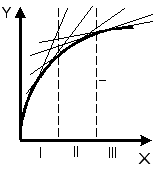
I:k₁x+b₁ - линейный участок

II:k₂x+b₂- «колено»

III:k₃x+b₃– режим насыщения

3. Вместо определения частных производных (формулы 11 и 11’) вводят переменные в исходные нелинейные уравнения в следующем виде:

Следует помнить, что ,,являются функциями времени (т.е. не зависят от времени).

- базисные точки или номинальный режим.

(13)

опорное движение (14)

4. Основан на определении коэффициентов линейного уравнения (апроксимирующего выражения) по методу наименьших квадратов для функции, задаваемой таблично. Таблицы заполняются в режиме нормальной эксплуатации объекта:

y=f(x₁,x₂) – зависимость в общем виде, а мы хотели получить:

(15)

В результате получаются формулы:

(16)

(17)

Глава 5 моделирование систем автоматического управления

§ 5.1. Методы моделирования и их применение в сапр

Под моделированием какого-либо объекта (явления, системы, устройства, знакового образования) обычно понимается воспро­изведение и исследование другого объекта, подобного оригиналу в форме, удобной для исследования, и перенос полученных сведе­ний на моделируемый объект. При этом объекты считаются по­добными, если характеристики процессов, происходящих в каком-либо из них, отличаются от соответствующих характеристик дру­гого объекта вполне определенными и постоянными в течение данного процесса коэффициентами. Модель изучаемого явления (объекта) при этом может быть иной физической природы, отличной от природы оригинала. Это обстоятельство открывает широ­кие возможности для применения моделирования в проектирова­нии, обусловленные привлечением таких эффективных его средств, как ЭВМ, динамические стенды, различного рода имитаторы и тренажеры.

Существуют различные методы моделирования: геометриче­ское и физическое моделирование, моделирование путем прямых аналогий, математическое моделирование на аналоговых и циф­ровых вычислительных машинах (АВМ и ЦВМ), полунатурное моделирование.

Каждый из этих методов имеет свои достоинства и недостат­ки. Применение того или иного метода определяется в каждом конкретном случае в зависимости от исследуемой системы и усло­вий ее работы. При этом необходимо иметь набор правил и усло­вий, выполнение которых обеспечивает требуемую точность изу­чения заданного объекта по его модели. Эти правила и условия формулируются в теории подобия.

На основе анализа перечисленных методов моделирования в соответствии с требованиями, предъявляемыми к «инструментам САПР» (см. § 1.1), в состав САПР САУ вводятся моделирование на ЭВМ (АВМ и ЦВМ) и полунатурное моделирование. В послед­нем случае с помощью средств САПР осуществляется не только воспроизведение и исследование объекта, но и управление про­цессами полунатурного моделирования (применение полунатур­ного моделирования в составе САПР для проектирования САУ рассматривается в гл. 10).

При математическом моделировании, моделировании на ЭВМ, в качестве объекта моделирования, оригинала, выступают исход­ные уравнения, представляющие ММ объекта, в качестве моде­ли — процессы, протекающие в соответствии с этими уравнениями и воспроизводимые на ЭВМ в виде «машинных решений» либо аппаратурно (АВМ), либо путем реализации программ (ЦВМ),

Математическое моделирование САУ осуществляется на АВМ и ЦВМ, поэтому часто такие способы называют аналоговым и цифровым моделированием. АВМ применяются в САПР САУ как консольные, терминальные, устройства на рабочих местах разра­ботчиков и испытателей. Управление АВМ осуществляется через терминальные станции центральным процессором в соответствии с общей идеологией построения САПР САУ (см. § 2.1). В даль­нейшем будем применять термин ЭВМ, понимая под ним только ЦВМ — основу технических средств САПР.

В математическом моделировании выделяют имитационное моделирование, под которым понимается воспроизведение процес­сов, объектов, явлений с имитацией случайными величинами и случайными процессами звеньев оригинала, которые не удается представить определенными ММ. Имитационное моделирование рассматривают так же, как управляемый эксперимент, произво­димый на ЭВМ. В таком эксперименте определенные математиче­скими моделями части объекта моделирования взаимодействуют с имитирующими возмущающие воздействия и некоторые звенья САУ генераторами случайных величин. Это взаимодействие про­водится по определенным в эксперименте правилам, а результаты моделирования подвергаются статистической обработке. Так, при моделировании ЛА по полной ММ, представленной на рис. 4.5, воздействие на него со стороны других внешних факторов миро­вого пространства — атмосферы, звезд, полярного сияния, косми­ческой пыли — имитируется генераторами случайных величин и процессов, а обработка результатов моделирования проводится на ЭВМ по специальной программе (см. гл. 6).

Под полунатурным моделированием (моделированием с реаль­ной аппаратурой) понимают исследование элементов реальной аппаратуры совместно с моделью остальной части системы, реа­лизованной на ЭВМ.

Применение такого метода моделирования становится необхо­димым в тех случаях, когда не удается описать работу некоторых элементов системы математически.

При полунатурном моделировании систем управления подвиж­ных объектов возникает необходимость моделирования в нату­ральном масштабе времени движения устройств САУ с целью влияния их кинематики и динамики на работу САУ в целом, при­чем ряд элементов этой САУ не поддается математическому опи­санию и реализуется аппаратурно.

В этой главе излагается математическое моделирование как один из инструментов САПР. Этот инструмент включает в себя соответствующие компоненты основных обеспечении САПР и слу­жит для воспроизведения и исследования САУ и их устройств на ЭВМ с целью эффективной замены макетирования на всех этапах проектирования САУ. Так, математическое моделирование динамики САУ позволяет значительно уменьшить объемы макет­ных испытаний и осуществить:

решение, таких проектных задач, как анализ функционирова­ния САУ, их устройств и элементов;

исследование влияния изменения параметров и возмущающих воздействий на стабильность характеристик САУ, выбор струк­турной схемы САУ по задаваемым проектировщиком критериям;

оценки устойчивости, динамических и статических ошибок для различных значений параметров выбранной структурной схемы и возмущающих воздействий.

Основное требование к подсистеме моделирования САПР САУ — создание более эффективного по отношению к макетиро­ванию инструмента для решения перечисленных проектных задач.