§ 3.3. Математическое обеспечение

Математическое обеспечение САПР включает в себя математические модели объектов проектирования, методы и алгоритмы.

Раскроем понятия, введенные в этом определении. Математическая модель — это система математиче­ских соотношений: аналитических в виде уравнений, графических в ви­де структурных схем или графов, табличных в виде таблиц, описы­вающих изучаемый процесс или явление.

Метод (греч. methodos) — путь исследования решения задачи, включающий в себя совокупность теории и приемов, содержащих ло­гику и обоснование решения зада­чи. Из метода решения вытекают алгоритмы.

Слово «алгоритм» (лат. algorithm} от арабской интерпретации имени узбекского математика IX в. Аль-Хорезми) означает совокупность правил, определяющих процедуру решения задачи по заданным исходным данным, которая заканчивается результатом, решением.

В САПР САУ математические модели являются необходимой составляющей для осуществления проектных процедур, состоящих во взаимодействии множеств М, О, К (см. ранее). ММ в большей степени определяют наиболее важные характеристики САПР САУ — время проектирования с помощью САПР, объем технических средств и обеспечении САПР, качество проектирования.

Математические модели САУ можно классифицировать по степени детализации САУ как сложной системы в соответствии с трехуровневой иерархической схемой, представленной на рис. 16 а. Тогда выделяются следующие три уровня ММ:

ММ всей САУ как сложной системы Р;

ММ устройств САУ как отдельных систем а _i

ММ элементов этих устройств как подсистем В_ij.

На рис. 16, б для иллюстрации такой иерархии ММ показаны уровни и соответствующие формы ММ: для САУ ЛА, например, гиростабилизатора (см. рис. 7 пример 2.2) и чувствительного элемен­та гиростабилизатора — гироблока с гироскопом на «газовом под­весе».

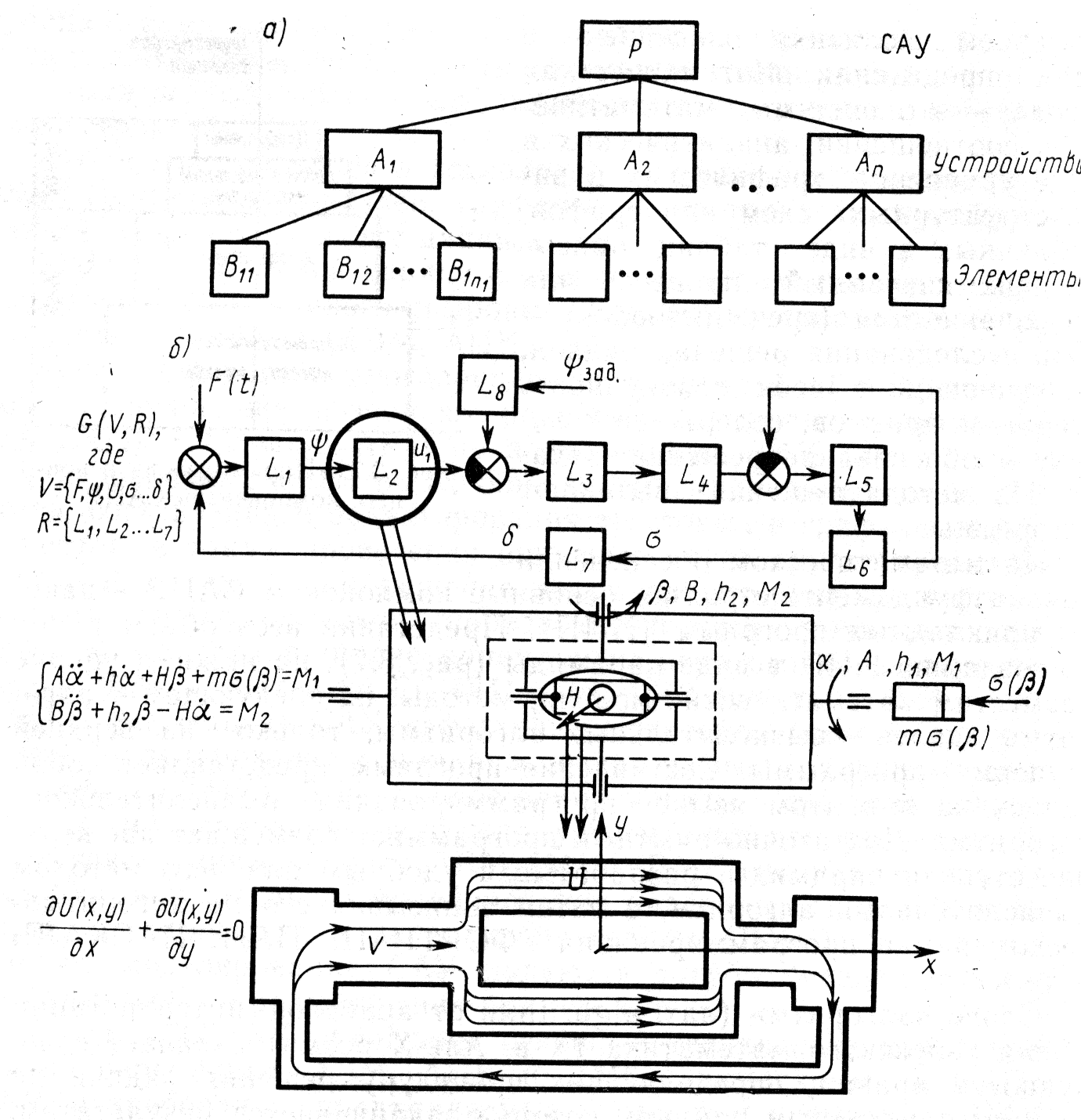
Рис.16. Уровни классификации математических моделей САУ

а – иерархическая модель, б – модель структуры, устройства и элемента

На самом верхнем уровне наибольшее распространение в тео­рии САУ получили ММ в виде структурных схем и графов G(V, R). Структурной схемой САУ называют ее графическое изображение в виде соединений звеньев. Звено обычно изобража­ют в виде прямоугольника с указанием оператора, связывающего входные и выходные сигналы. Такими операторами являются (на рис. 16, а они обозначены L₁—L₇ в соответствии с устройствами САУ ЛА) передаточные функции, дифференциальные и другие уравнения звеньев. Сравнивающие и суммирующие элементы струк­турной схемы отображают в виде круга. Полагая, что читатель достаточно осведомлен о правилах преобразования структурных схем САУ, представим рис. 17, а, б, на котором после выполнения соответствующих элементарных преобразований построены струк­турные схемы, соответствующие САУ ЛА по углу тангажа θ (на рис. 17, а Т₁ = Т₂ = 1) и САР ТГ с указанием простейших матема­тических моделей отдельных устройств — передаточных функций. На рис. 17, б отдельные звенья соответствуют САР ТГ, описание которой приведено в примере (см. номера звеньев на рис. 1 и 17, б). Причем рассмотрены два канала этой САР: регулиро­вание частоты вращения турбины (РЧВ) и регулирование давле­ния пара (РДП). Из математических моделей, представленных на рис. 17 в виде структурных схем, видно, что они могут не со­ответствовать «естественному» разделению звеньев. Некоторые естественные звенья «математически» объединяются в одно, а другие, наоборот, разделяются. Так, устройства ТГ 4, 4' раскрыты более подробно. Это делается для удобства дальнейших исследо­ваний САУ уже по ее ММ, т. е. по некоторому абстрактному об­разу этой САУ. На основании структурных схем возможно по­строение алгоритмов, анализа и синтеза САУ с дальнейшей их программной реализацией на ЭВМ. При построении соответст­вующих инструментов САПР потребуется специальный проблем­но-ориентированный язык разработчика САУ, на котором он будет производить необходимые операции со структурными схемами — определение передаточных функций разомкнутой и замкнутой це­пей, преобразование многоконтурной цепи к одноконтурной, пред­варительные расчеты САУ. На основе структурных схем прово­дится исследование САУ в целом: формируются ее облик и функ­циональная схема, осуществляется выбор устройств.

Удобным для исследования отображением структурных схем САУ являются ориентированные графы, которые применительно к САУ обладают следующими свойствами:

— дуги графа изображают звено и характеризуются операто­ром этого звена — передаточная функция, уравнения звена;

— каждой вершине ставится в соответствие одна из перемен­ных, и в соответствии с правилами работы с графами вершина, к которой подходит одна или несколько дуг, соответствует пере­менной, равной выходу одной дуги или сумме выходов дуг. Если из вершины исходит несколько дуг, то входная величина для всех этих дуг одна и та же.

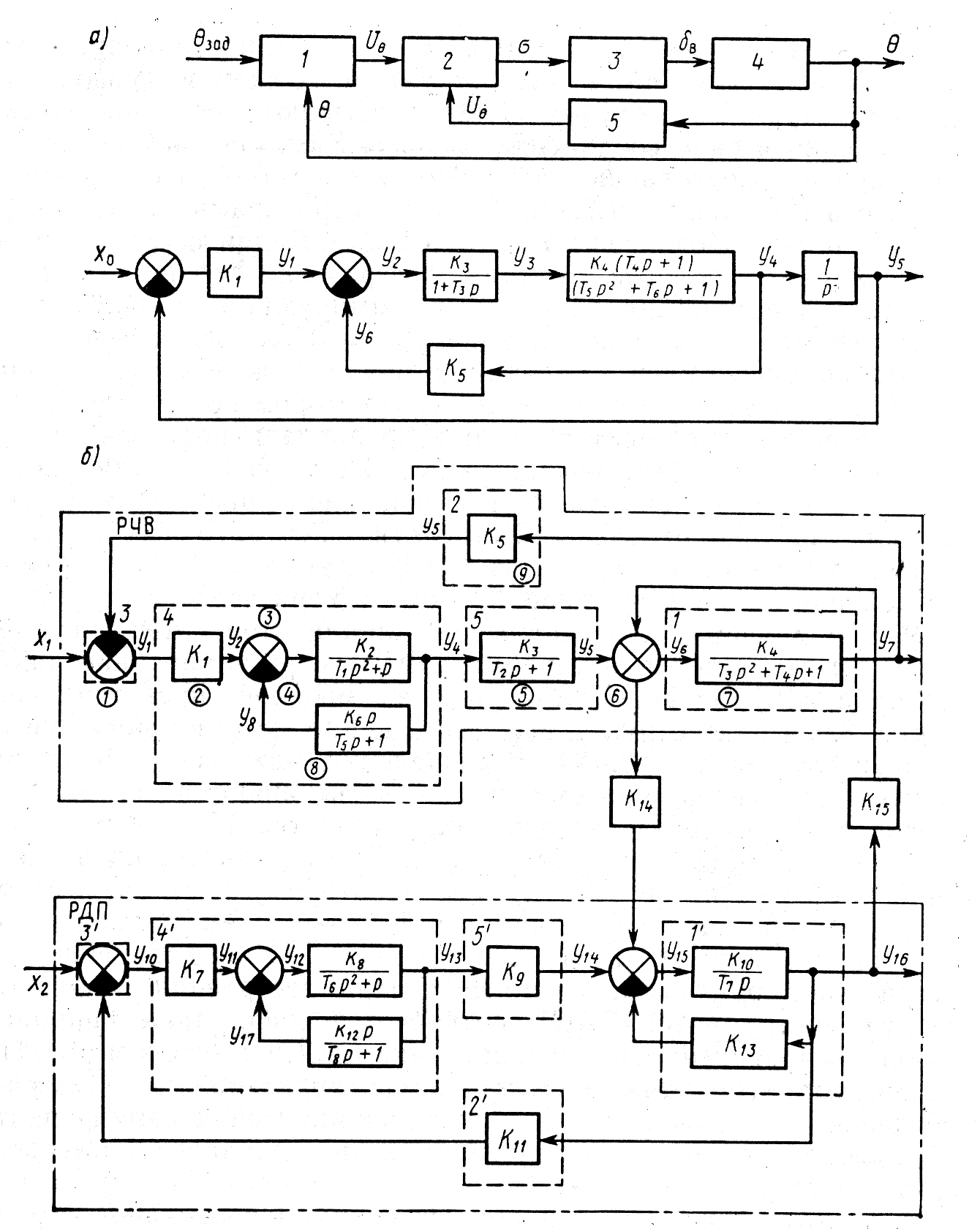
Рис. 17. Структурные модели САУ:

а — структурные модели САУ летательного аппарата; 1 — датчик угла тангажа; 2 — усилитель;

3 - рулевая машина руля высоты; 4 — планер, корпус самолета; 5 — датчик угловой скорости;

б — структурные модели САУ турбогенератора

На рис. 18 показаны графы, построенные по структурным схемам САУ, приведенным на рис. 17. Правила работы с графа­ми во многом сходны с правилами преобразований структурных схем. Так, простой путь на графе, если нет не принадлежащих ему дуг, можно заменить одной дугой с передаточной функцией, равной произведению передаточных функций дуг этого пути. Па­раллельные дуги можно заменить одной дугой, равной сумме пе­редаточных функций этих дуг.

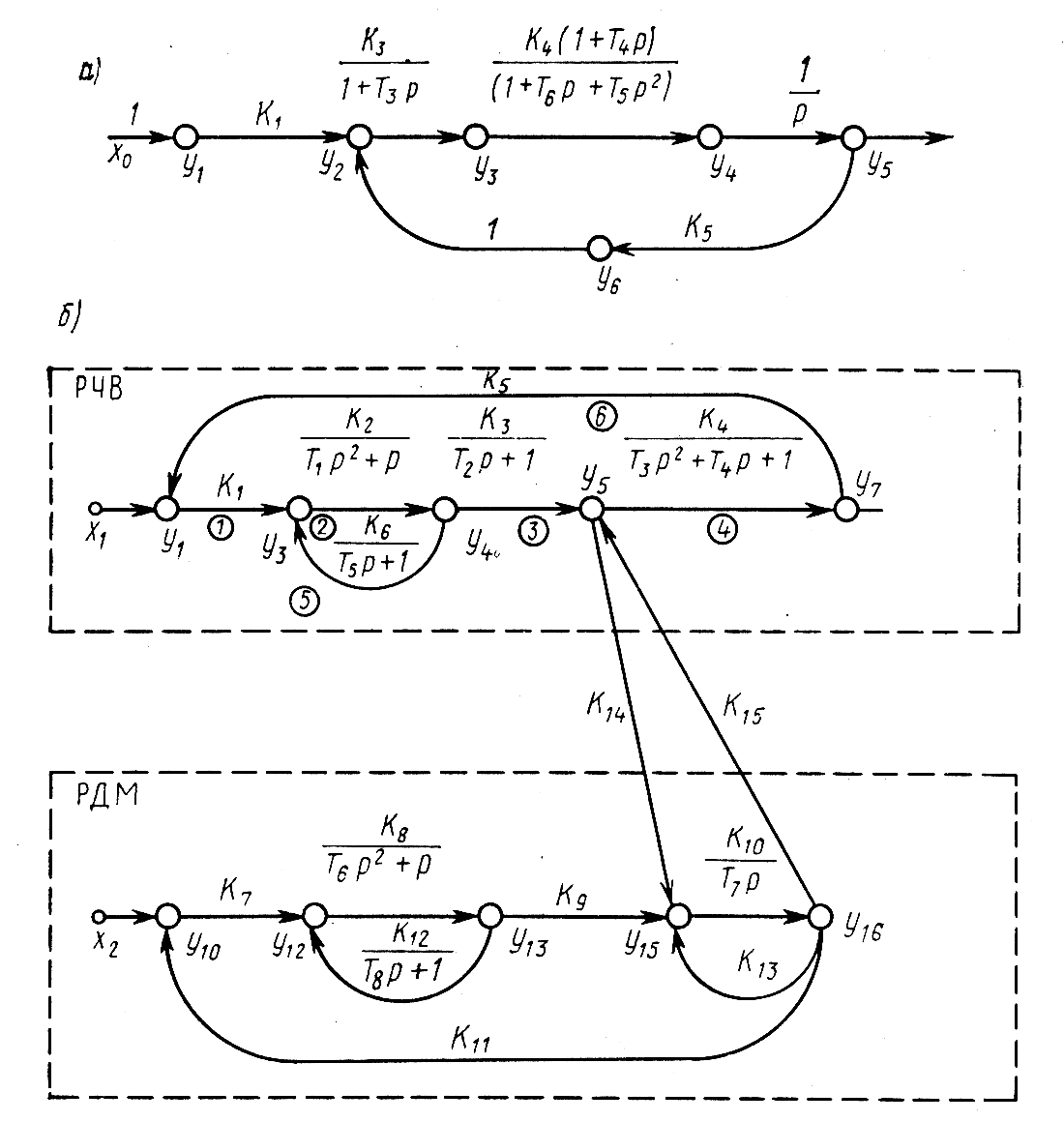
Рис. 18. Графы САУ самолета и турбогенератора

Определение передаточной функции САУ по ее графу можно выполнить пользуясь формулой Мейсона [16]:

(3.6)

где W_i — передаточная функция i-го простого пути от вершины y_i к вершине у_k, равная произведению передаточных функций, входящих в этот путь; т — общее число таких путей; Δ — опреде­литель графа;

где Wj⁽¹⁾ — передаточная функция j-го контура; N — количество контуров; Wj⁽²⁾ — произведение передаточных функций, не касаю­щихся, т. е. не имеющих общих дуг и вершин пар контуров; Wj⁽³⁾ — произведение передаточных функций, не касающихся тро­ек контуров, и т. д.; Δ_i— определитель подграфа, получающийся из исходного графа при удалении дуг и вершин i-го простого пу­ти, а также всех дуг, инцидентных этим вершинам.

Перейдем теперь к «раскрытию содержания» операторов ма­тематических моделей описания САУ верхнего структурного уров­ня, т. е. к ММ устройств САУ (второй уровень иерархии ММ САУ, рис. 16, а).

Общепринятой формой ММ многих устройств САУ, а также объектов управления являются обыкновенные дифференциальные уравнения, в общем случае нелинейные, стохастические, с запаз­дывающим аргументом. Из этих уравнений как частные случаи получают линейные алгебраические, дифференциальные и другие уравнения.

Так, на рис.16, б приведены линейные дифференциальные уравнения гиростабилизатора с традиционными обозначениями: А, В — моменты инерции; h₁, h₂— коэффициенты вязкого трения; H— кинетический момент гироскопа; α, β — углы стабилизации и прецессии.

В общем случае ММ устройств САУ можно представить в ви­де системы из обобщенных стохастических обыкновенных диффе­ренциальных уравнений второго порядка:

(3.7)

где при t=0, Y(0), Y’(0) —векторы из начальных условий случай­ных величин, f принадлежит отрезку [0, T]; F* — вещественная нелинейная вектор-функция своих аргументов; F*= (F₁*, F₂*, ...,F_n1*)' ; Y=(y₁,... ...,y_n)' ; Y, Y’, Y’’— векторы из фазовых координат и их производ­ных 1-го и 2-го порядков — случайных функций времени; Х= = (x₁,... ,х_n)' — вектор из возмущающих воздействий на систе­му— случайных функций времени; U= (u₁, ...,и_п)' — вектор из уп­равляющих воздействий на объект управления — случайных функ­ций времени. Такие уравнения обычно выводятся с помощью клас­сических способов аналитической динамики (см. гл. 4).

Управляющие воздействия часто формируются в виде отдель­ных дифференциальных уравнений, связывающих векторы X, Y и U и их производные:

(3.8)

где U(0), U’(0)—начальные условия; Ф* — вещественная нелинейная вектор-функция своих аргументов порядка n3; R= (r₁, r₂,...,r_n)—вектор из коэффициентов, устанавливаемых при фор­мировании управлений; Δλ= (λ₁,... , λ_n4)—вектор параметров — случайных величин. Параметрами ММ САУ будем считать состав­ляющие коэффициентов дифференциальных уравнений, несущие определенный физический смысл (например, моменты инерции, коэффициенты усиления, постоянные времени).

В дополнение к перечисленным составляющим системы (3.7) будем считать заданными вероятностные характеристики случай­ных функций X(t) и случайных величин Y₀, Y’₀, U₀, U’o, Δ, R, ξ_x[X(t)], ξ _YO(Yo), ξ _Y’O(Y’o), ξ (U₀), ξ (U’₀),, ξ_λ (λ),. которые в частных случаях выражают математические ожидания, дисперсии, плот­ности распределения вероятностей случайных величин

Система (3.7), (3.8) является достаточно общей, и из нее мож­но получить обычно распространенные формы ММ устройств САУ как частные случаи.

Рассматривая промежутки времени t_k—t_k-1 принадлежит промежутку [0, Т], на кото­рых случайные функции времени и случайные величины в (3.7), (3.8) можно заменить их математическим ожиданием (в дальней­шем для простоты будем рассматривать только уравнение (3.7)), систему (3.7) можно разбить на S подсистем с детерминирован­ными аргументами функции F*:

(3.9)

Положим для простоты дальнейшего изложения F_k* = F и при­ведем эту систему к нормальной форме. Для этого необходимо осуществить замену переменных и разрешить систему (3.9) относительно старшей произ­воднойY’’. Тогда получимнормальную форму нелинейных обыкно­венных дифференциальных уравнений

(3.10)

с начальными условиями Y(0), где Y= (y₁ ..., у_п1,), Х= (х₁, ...,х_n2), U=(u₁,...,u_n3), Λ= (λ₁,... , λ_n4) F=(F₁,...,F_n1) —соответствую­щие (3.10) векторы, n₁ = 2nl. Система дифференциальных уравне­ний в форме (3.10) называется системой в форме Коши (А. Л. Коши — французский математик, 1789—1857). При дальнейшем уп­рощении уравнений (3.10) правые части в (3.10) заменяются на приближенные выражения

получаемые после линеаризации нелинейностей f_j относительно установившихся значений переменных Y_0, X₀. При этом осущест­вляется известная замена Y=Y₀+ΔY, Х=Х₀+ΔХ, где Y_0, X₀— установившиеся программные значения переменных, известные функ­ции времени или постоянные величины, а. ΔY, ΔХ — малые откло­нения в процессе движения. После такого упрощения получим распространенную форму — линейные обыкновенные дифференци­альные уравнения с постоянными или переменными во времени коэффициентами

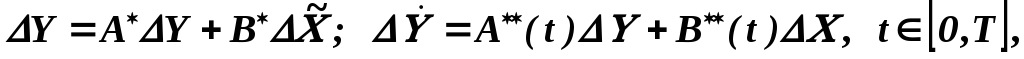(3.11)

где А*, В*, А**, В** — матрицы из коэффициентов а_ij, Ь_ij.

В некоторых случаях при описании САУ и их устройств при­меняется форма ММ вида

(3.12)

и происходящие от нее линейные относительно y₁,...,y₁⁽ⁿ⁾ MM

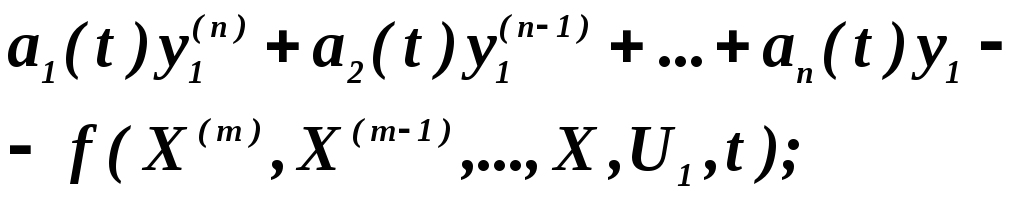(3.13)

(3.14)

где Х^(m), Х^(m-1)>... — производные порядка т, т—1, ... от вектора X; a₁(t),..., a_n(t), a₁,...,a_n— переменные во времени и постоянные ко­эффициенты; u₁—управляющее воздействие по координате у₁.

Такие ММ используются в том случае, когда при исследовании требуется определить процессы только по одной координате, в данном случае y₁(t), а все остальные составляющие вектора Y— — (y₂(t), … ,y_п(t)) интереса не представляют.

Для удобства исследования устройств и САУ в целом на ЭВМ систему (3.7), (3.8) после линеаризации, аналогичной (3.11), представляют в форме

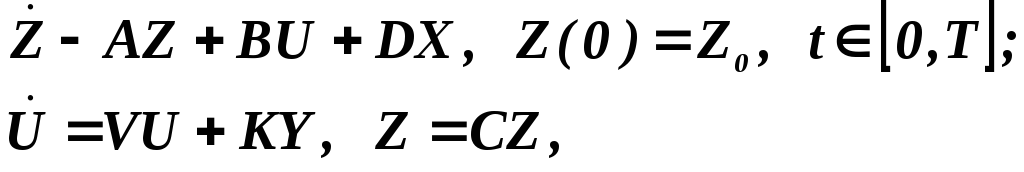(3.15)

где Z — вектор из координат «внутренних» состояний системы; U — вектор управляющих воздействий; Y — вектор «выходных ко­ординат»;

К=(k_ji)^n2m, С= (с_ji)^{т, т} — прямоугольные матрицы коэффициен­тов при векторах Z, U, возмущающих воздействиях X, коэффици­ентов, формирующих законы управления САУ и связи векторов Y, Z. Как правило, рассматриваются случаи, когда матрицы А, В, С, D, V, К содержат только постоянные элементы. Уравнения (3.15) получили распространение под названием формы про­странства состояний.

Если функции Y(t), U (t) и их производные, входящие в формы (3.7) — (3.15), в принципе имеют запаздывание Y(t—τ), U(t—τ), то эти уравнения будут уравнениями с запаздывающим аргумен­том, отображающими, в частности, динамику гидравлических, пневматических и микропроцессорных элементов САУ.

Модели (3.7) — (3.15) служат основой для построения операто­ров L в ММ высокого ранга (см. рис. 16). В частности, из диф­ференциальных уравнений (3.15) получим

(3.16)

В этом операторном уравнении вектора Y, U, X те же, что и в (3.15), a L(p), G(p), R(p) —операторы из полиноминальных мат­риц вида

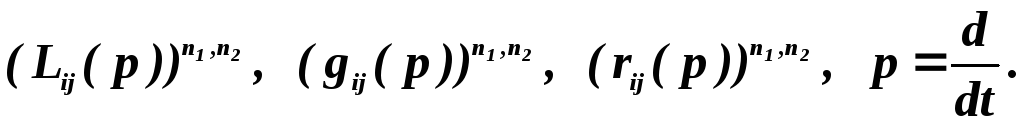
Из (3.16) в простейшем случае можно получить скалярное уравнение

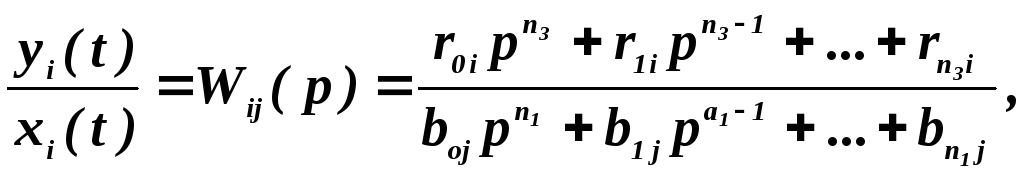(3.17)

т. е. передаточную функцию — известный в теории САУ оператор.

Нелинейные дифференциальные уравнения также могут быть представлены в операторной форме. Так, уравнение- (3.10) пред­ставляется в операторной форме на основе разложения выходной ко­ординаты Y в ряды Вольтерра. Для одномерного случая перемен­ной y_i и воздействий U_j ,x_j такое разложение после объединения U_j(t) и x_j(t) в одно возмущающее воздействие x_j*(t) имеет вид

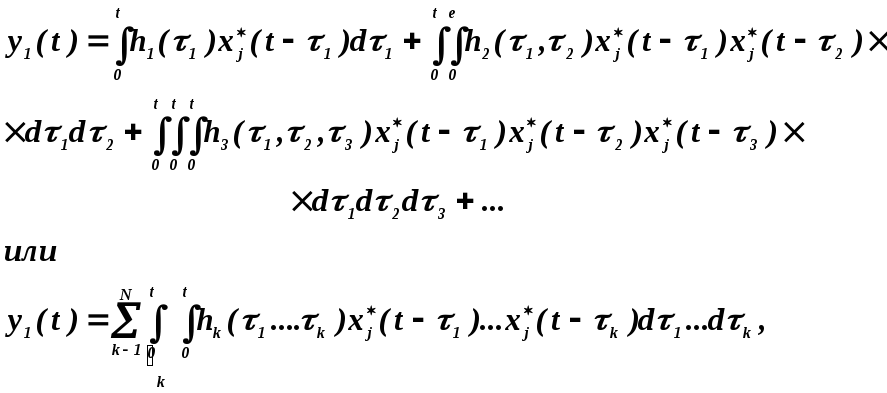(3.18)

где h_k(τ ₁, …, τ _k) —обобщенные весовые функции исследуемой не линейной системы, получаемые после приведения исходного урав­нения (3.10) к интегральной форме

применения к этой форме разложения Вольтера;

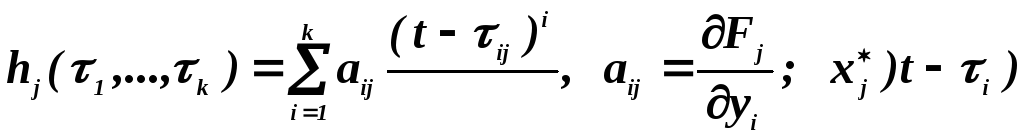
— значения входного сигнала, отстоящего (запаздывающего) от момента времени t на величину τ _i

Формы ММ (3.7) — (3.18) являются достаточно общими для отображения различных устройств САУ. ММ непрерывных процес­сов в САУ и их устройствах описываются уравнениями (3.7) — (3.18) без каких-либо изменений. ММ дискретных устройств САУ получаются из уравнений (3.7) — (3.18) как частный случай, когда функции в них определены только при t_n=nT, где Т — такт дис­кретности по времени, а п=0, 1, 2,....

В отличие от непрерывных ММ дискретные модели устанав­ливают соотношения между решетчатыми функциями

(3.19)

значения которых могут быть определены не в любой момент вре­мени. Для решетчатых функций вводятся понятия квантования по времени (Т) и квантования по уровню (Δ). ММ дискретных си­стем представляются в форме разностных уравнений. Переход от исходных дифференциальных уравнений к эквивалентным разност­ным можно сделать не единственным способом. В частности, по­лагая, в уравнениях (3.10)

получим обобщенные разностные уравнения в векторной форме:

(3.20)

Напомним, что в общем случае разностное уравнение n-го по­рядка записывается при Т=1 в виде

(3.21)

где под конечной разностью Δy(n) понимается выражение

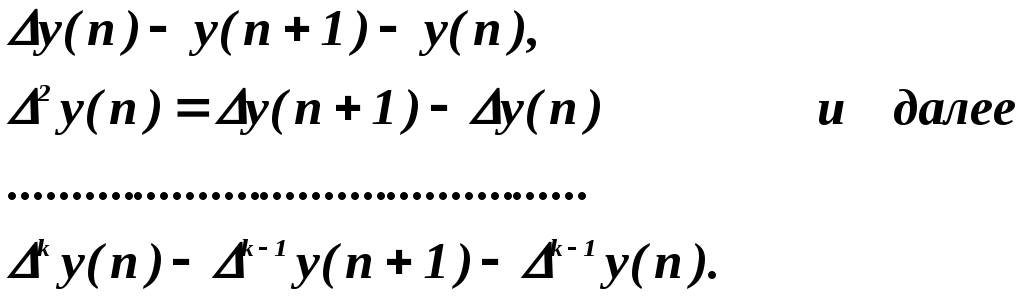
Раскрывая эти выражения получим

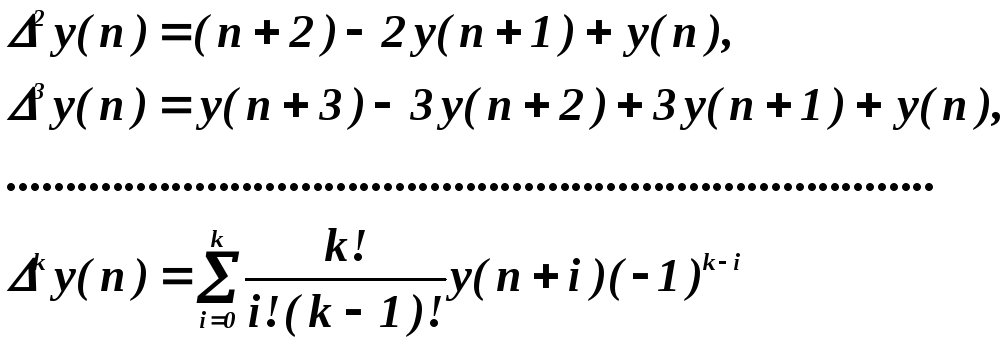(3.22)

После подстановки (3.22) в (3.21) приходим к разностному урав­нению k-то порядка в форме

(3.23)

Если это уравнение удается представить в виде

то, очевидно, задав начальные значения при n=0, y(0), y(1),..., y(k—1), мы получим у _k и вообще у_п при любом целом п.

Уравнение (3.23) представляет собой разностный аналог фор­мы Коши (3.10) и позволяет рекуррентно (последующее значение у(п) через предыдущее) вычислить все интересующие значения y(п).

Возвращаясь к форме представления САУ в «пространстве со­стояний» (3.15), представим ее в конечно-разностном виде (3.23) другим способом. Решение первого уравнения из системы (3.15), можно записать в известной форме

Положим в этом уравнении t_o = nT, t—(n+1)T и рассмотрим промежуток времени nT<τ<(п+1)Т. Будем также считать, что Z₀=Z(nT), U(τ) = U(nT), Х(τ)=Х(nT). Тогда вместо (3.24), по­лучим

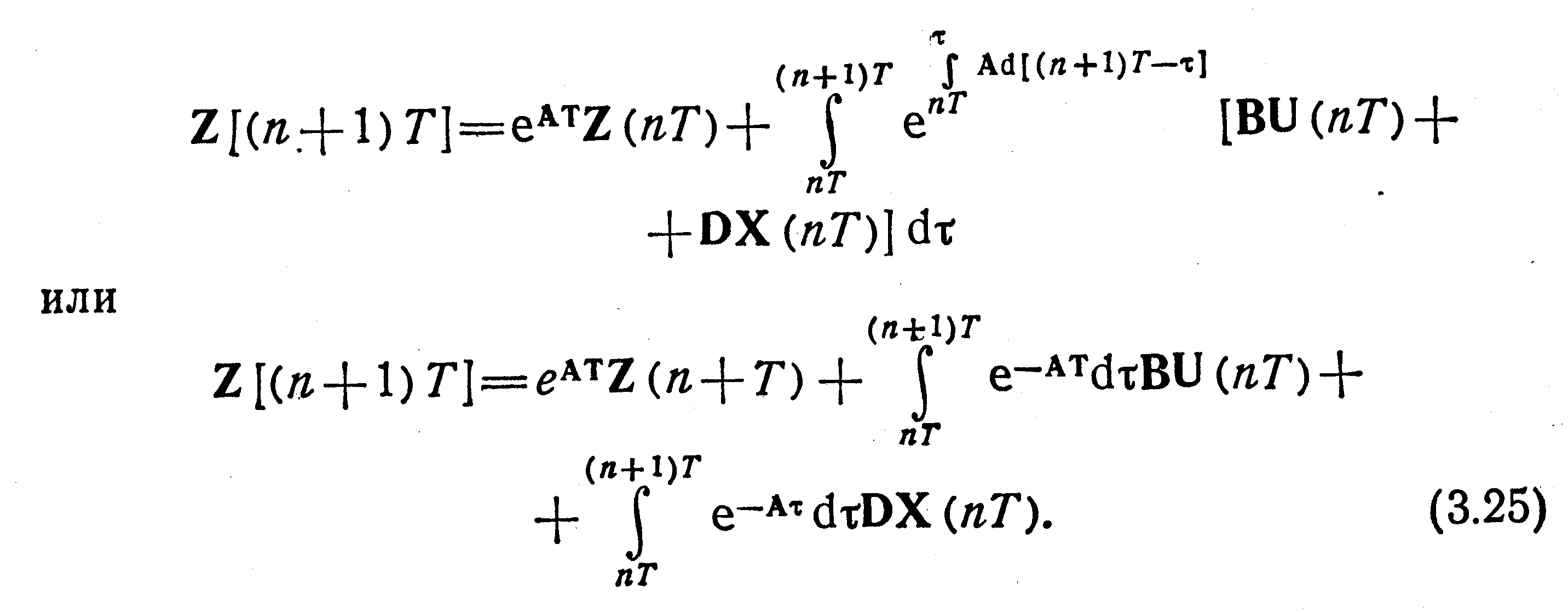
Аналогично приводится к разностной форме второе уравнение системы (3.15), а третье уравнение примет вид Y(nT)=GZ(nT). ММ в форме (3.25) применяется при исследовании как непрерыв­ных, так и дискретных САУ и ее устройств.

Разностные уравнения, аналогично формам (3.17), (3.18), мож­но представить в операторной форме. Так, если в уравнении (3.25) обозначить

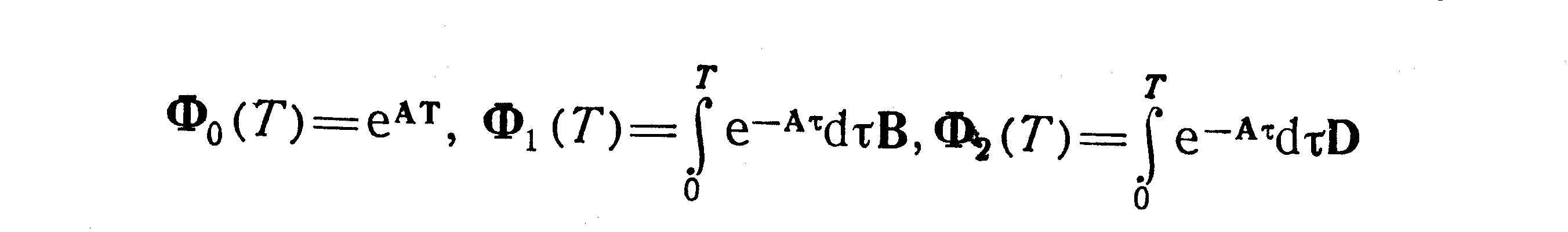
и ввести оператор сдвига 2=е^Tр, где р — оператор Лапласа, на основании известной в теории операционного исчисления теоремы упреждения, то получим операторное уравнение в виде

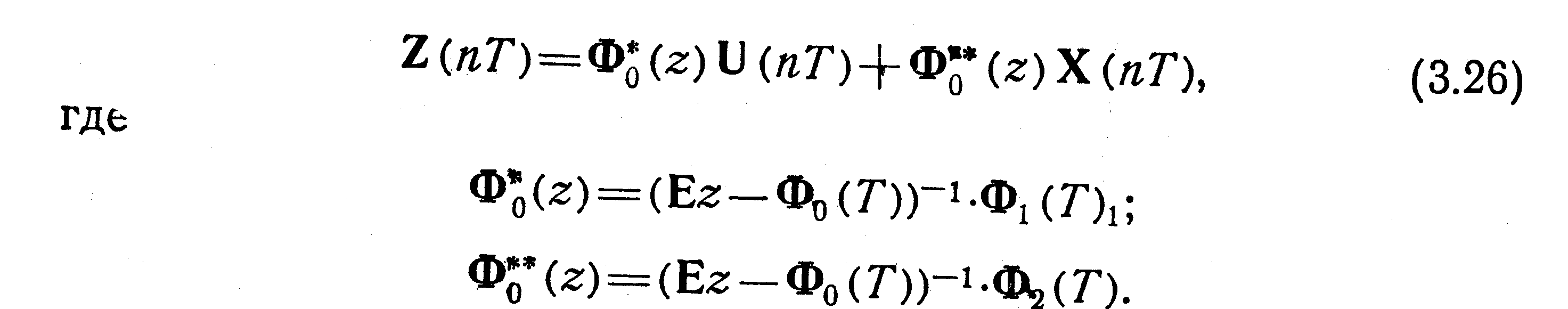
Из (3.26) в простейшем случае можно получить скалярное уравнение

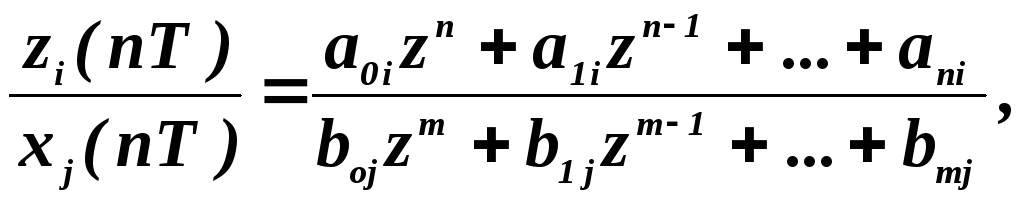(3.27)

z — передаточную функцию — известный в теории САУ оператор, широко применяемый для анализа дискретных систем.

Таким образом, ММ (3.7) — (3.27) могут служить для решения задач в процессе проектирования устройств, соответствующих раз­личным классам САУ: стохастическим и детерминированным, не­линейным и линейным, нестационарным и стационарным, непре­рывным и дискретным.

ЭлементыСАУ при первоначальном их получении описыва­ются ММ на уровне представления физических явлений. Многооб­разие физических явлений, лежащих в основе многих элементов САУ, затрудняет построение каких-либо общих их ММ, поэтому рассмотрим некоторые типовые ММ, соответствующие частным случаям обобщенного дифференциального уравнения в частных производных второго порядка:

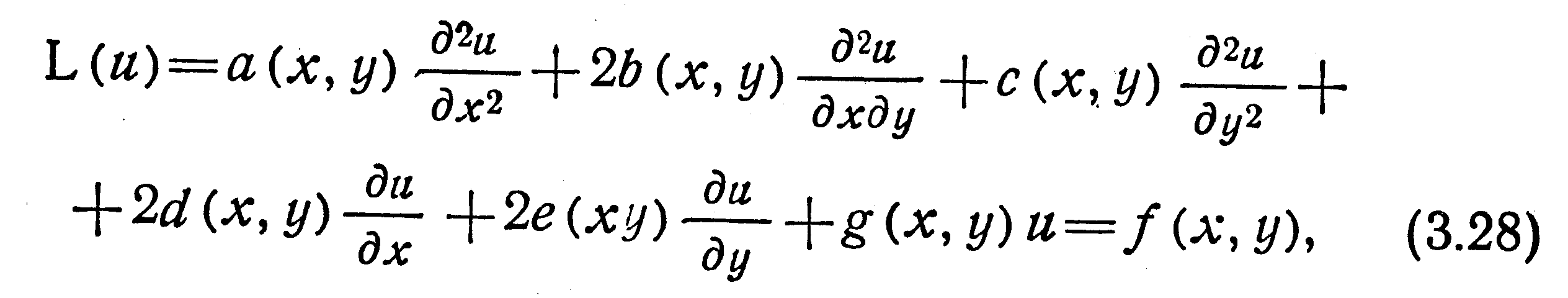
где а(х, у), b(х, у), с(х, у), d(x, у), е(х, у), g(x, у) — коэффициенты; f(x, у)—свободный член уравнения. Эти функции от неза­висимых переменных x, у заданы в области D ограниченной кон­туром Г; и=и(х, у) —искомая функция, которая может быть на­пряжением механического элемента, потоком газа или жидкости в пневматическом и гидравлическом элементах САУ. Уравнение (3.28) называют эллиптическим, параболическим и гиперболиче­ским в зависимости от условий R(x, y)<0, R(x, y)=0, R(x, y)>0 для всех х, y принадлежащих области D. При этом R(x, у)=b²(х, у)—а(х, у). В за­висимости от типа уравнений задаются начальные и граничные условия, связанные с этими уравнениями.

Так, эллиптическое уравнение (уравнение Пуассона)

при известных граничных условиях может являться ММ механи­ческого вала турбогенератора, оси карданова подвеса ГСП, звена ноги ШР, вала привода рулевых исполнительных элементов ЛА. По этой модели определяется функция и(х, у), задающая момен­ты упругих сил, которые в дальнейшем учитываются в уравнени­ях (3.7) — (3.18) динамики всего устройства САУ в целом. Пара­болическое уравнение в простейшем случае для однокоординатной системы

применяется при расчетах распространения теплоты в одномер­ных элементах механических устройств САУ. При этом требуется найти U(x, t)—распространение температуры в зависимости от расположения источника тепла f(x, t) по отношению к измеряе­мой точке оси х в заданные моменты времени t. Гиперболическое уравнение (волновое уравнение)

применяется при расчетах пневматических и гидравлических эле­ментов САУ. В частности, распространение потока, обтекающего элементы корпуса ЛА, расчет давления газа в чувствительном элементе ГСП (см. рис. 16, б), расчет давления пара в ТГ про­водятся по ММ (3.31), а результаты расчета в виде функции и(х, у) используются в уравнениях (3.7) — (3.18) динамики соответст­вующих устройств САУ как возмущающие воздействия на систе­му— составляющие вектора X(t).

Вообще говоря, уравнения (3.28) являются более общими, чем (3.7) —(3.23). Из них можно получить обыкновенные дифферен­циальные и разностные уравнения как частные случаи. Однако последние используются на более высоком уровне иерархии ММ именно в силу своего большего «абстрагирования» от физики про­цессов в элементах.

При исследовании «собственно» дискретных элементов САУ (релейные, импульсные, элементы микропроцессоров) понятие «со­стояние» физически связано с «внутренним миром» этих элемен­тов. Различают однотактные и многотактные дискретные элемен­ты. В однотактных — элементах без памяти — совокупность выход­ных сигналов Y(nT) (n=0, N) представляет собой однозначную функцию входных сигналов Х(пТ) для того же момента времени, т. е. Y(пТ) =Ф[X(пТ)]. В многотактных — элементах с памятью — выходные сигналы зависят в данный момент времени t=nT не только от входных сигналов в тот же момент х(пТ), но и от со­стояния внутренних составляющих дискретного элемента z(n) в предыдущие моменты времени:

Однотактные дискретные устройства и элементы САУ описы­ваются булевыми функциями f (x₁,... ,х_п), где х₁,...,х_п при­нимают значения из множества {0, 1}. Имеется точно 2²ⁿ булевых функций от п переменных.

С помощью булевых функций однозначно определяется выход­ной сигнал дискретного устройства при заданных входных.

Многотактные дискретные устройства описываются матема­тическими моделями на основе конечных автома­тов. Конечный автомат характеризуется тремя множествами: входным алфавитом X; множеством входных дискретных сигна­лов; выходным алфавитом Y — множеством внутренних состояний Z. Функционирование конечного автомата описывается двумя функциями: функцией перехода в новое состояние δ и функцией выходов λ, т. е.

(3.32)

Если то вместо (3.32) получим

(3.32^*)

Выражения (3.32) определяют работу автомата Мили, а (3.32*) определяют автомат Мура.

С помощью автоматов Мили и Мура и таблиц переходов меж­ду элементами дискретной системы составляются ММ элементов таких устройств САУ, как БЦВМ в ЛА, микропроцессорные си­стемы регулирования в ГСП, регуляторы на микропроцессорах для роботов, турбин и др. С помощью ММ (3.28) — (3.32) опреде­ляются коэффициенты и параметры уравнений устройств (3.7) — (3.27), т. е. ММ более высокого уровня.

Перейдем к математическим методам и алгорит­мам как компонентам математического обеспече­ния САПР САУ. Поскольку подробное рассмотрение методов и алгоритмов как компонентов соответствующих инструментов САПР будет дано в последующих главах при изложении конкрет­ных подсистем САПР САУ, здесь мы рассмотрим классификацию, качественный состав методов и алгоритмов, а также остановимся на особенностях построения вычислительных алгоритмов в мате­матическом обеспечении САПР САУ. Одним из возможных под­ходов к классификации таких методов является их разбиение на машинно-ориентированные эвристические и классические методы теории САУ, «чисто» машинные и машинно-аналитические.

Попробуем раскрыть содержание каждого из этих методов При общих исследованиях САУ задача часто оказывается на­столько неопределенной, что приходится пользоваться эвристиче­скими методами (ЭМ). ЭМ — это такие методы, которые основа­ны на интуиции и опыте разработчика САУ.

В настоящее время ЭМ получили развитие благодаря внедре­нию диалоговых режимов работы «человек — ЭВМ», развитию методов по распознаванию образов, методов факторного экспе­римента и т. д. Структурно ЭМ функционируют по схеме, пред­ставленной на рис. 20, а.

При проектировании сложных САУ приходится иметь дело с тремя категориями условий и исходных данных при решении задач: определенно-детерминированными, определенно-вероятност­ными, неопределенными. В третьем случае имеются лишь некото­рые сведения о возможных законах распределения или об интер­вале возможных значений характеристик и параметров САУ. В этом случае единственно возможным оказывается эвристиче­ский подход, который, несмотря на неопределенность исходных данных и условий, позволяет на основе опыта, интуиции и экс­пертных оценок принимать решения при проектировании САУ. Машинная ориентация такого эвристического подхода сводится к построению алгоритма, который бы сочетал интуицию, опыт и эвристики человека с возможностью быстрой проверки на ЭВМ.

Классические методы созданы для анализа устойчивости ка­чества и точности САУ и ее устройств, решения задач синтеза регуляторов САУ и корректирующих устройств. Классические методы исследования и расчета САУ изложены в многочисленных работах по теории САУ и, как правило, представляют собой ска­лярные методы, предназначенные для простых систем невысокого порядка. Такой подход вполне оправдан тем, что при отсутствии ЭВМ проектирование САУ осуществлялось путем приближенных теоретических расчетов в сочетании с макетированием и испыта­ниями, которые составляли, да и сейчас еще составляют наиболь­шую часть инструментария проектировщика.

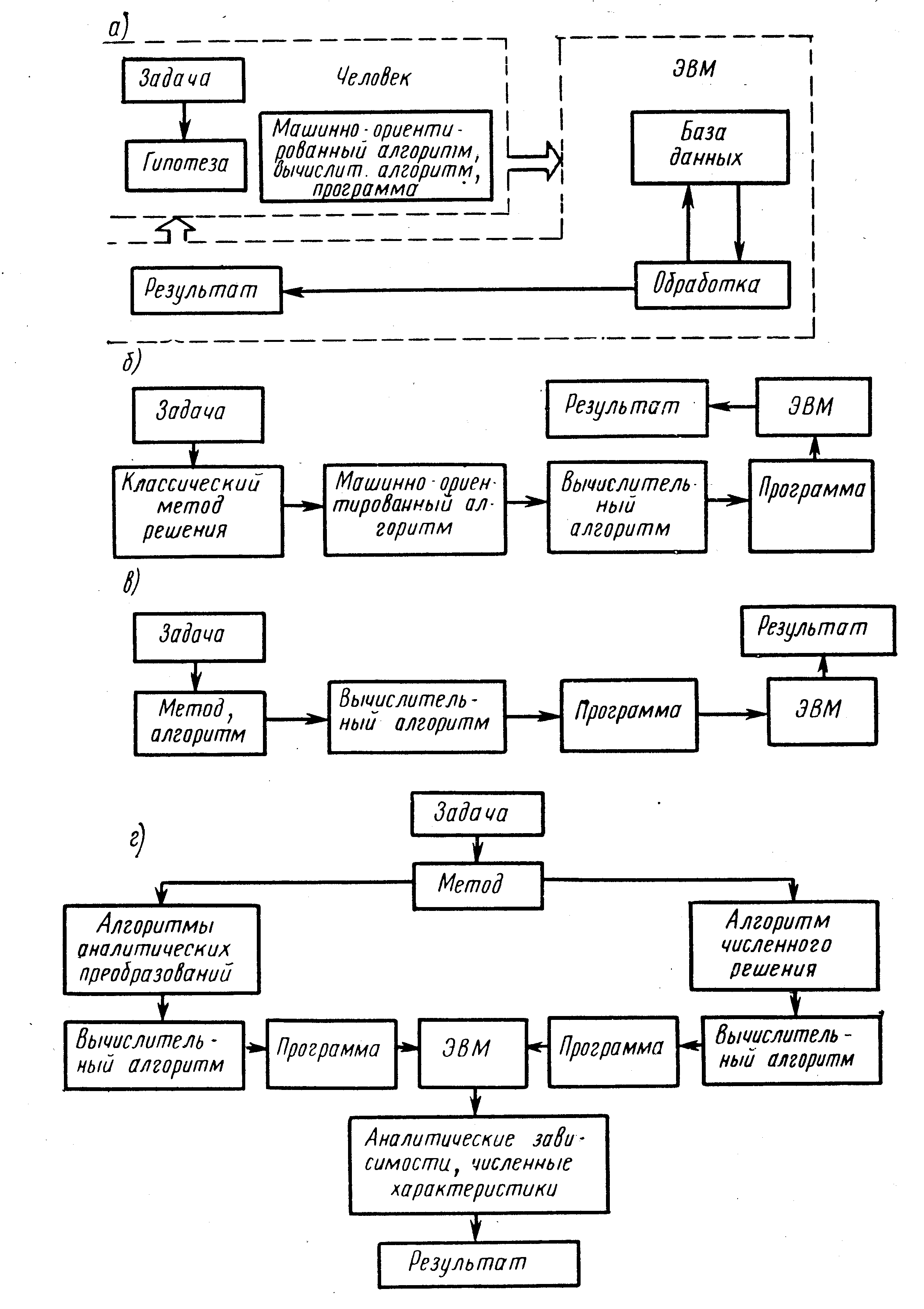
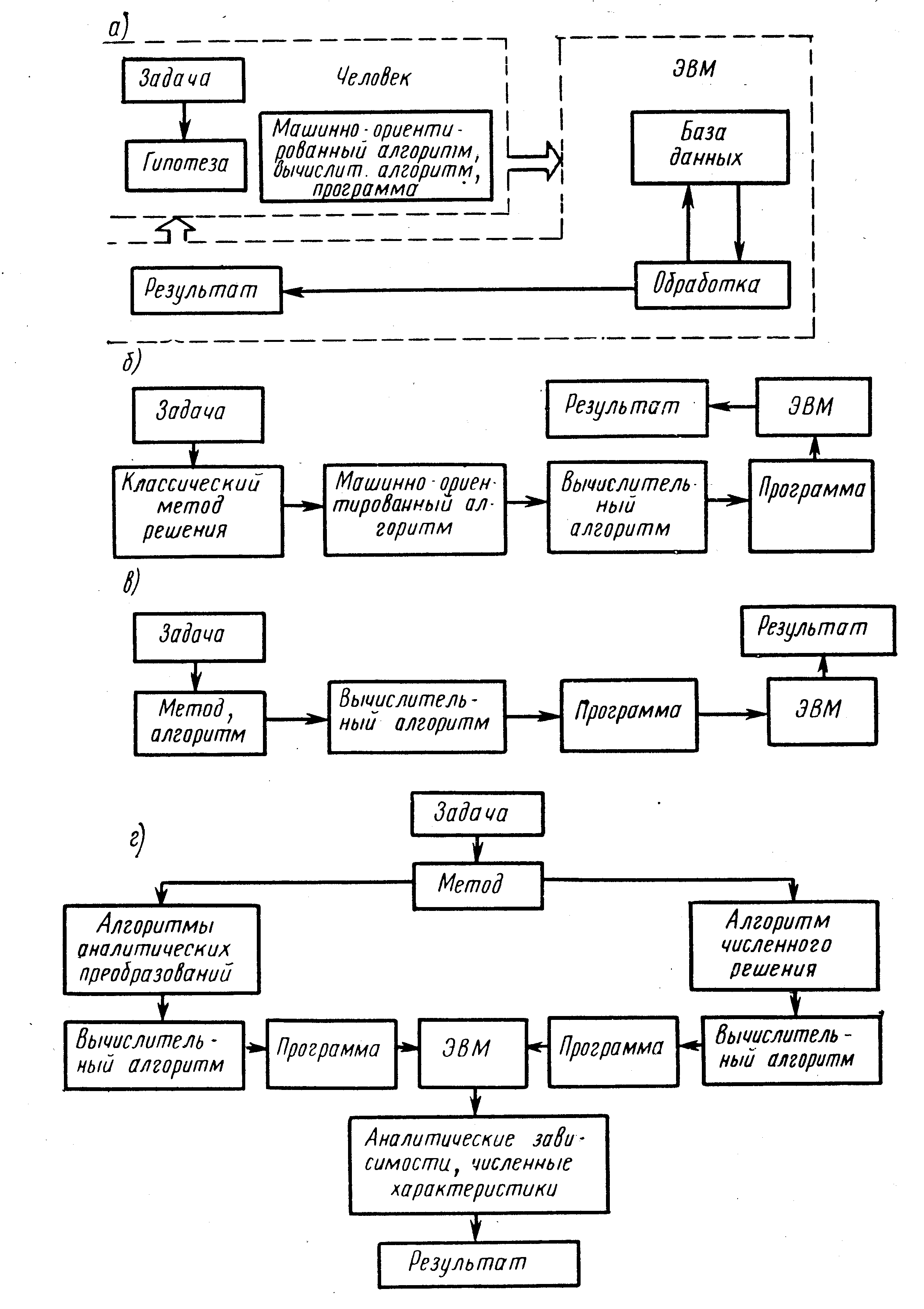
Рис.19. Функциональные схемы методов.

Машинная ориентация классических методов состоит в том, чтобы путем создания соответствующих алгоритмов распростра­нить их на системы высокого порядка, многомерные и многокри­териальные; оценки проводить не по одному, а по нескольким параметрам; упростить и ускорить процедуру получения конечных результатов; осуществить сервисное представление результатов, графиков, таблиц, расчетных данных с помощью внешних устройств ЭВМ.

Машинная ориентация классических методов теории САУ поз­воляет значительно ускорить процесс решения задачи, однако при этом не получается качественно новых методов и требуется определенная работа по созданию алгоритмов и вычислительных алгоритмов. Например, широко известный метод ЛЧХ при его реализации на ЦВМ не встречает особых трудностей для мини­мально-фазовых систем со слабыми резонансными свойствами. В случае неминимально-фазовых систем с резко выраженными резонансными свойствами вычислительные алгоритмы построения ЛЧХ значительно усложняются. Структурно машинно-ориентиро­ванные методы можно представить рис. 20, б.

С другой стороны, при машинной ориентации традиционных методов следует исходить из вычислительных возможностей ЭВМ. Если при «ручных методах» выбор того или иного подхода в ре­шении задачи — дело вкуса исследователя, то для реализации на ЭВМ вычислительные алгоритмы во многом определяют затраты машинного времени, сходимость вычислительного процесса и т. д.

К классическим методам за последние 30 лет добавились мно­гочисленные методы исследования и проектирования сложных современных САУ. Так, в связи с широким внедрением в САУ микроЭВМ, для синтеза регуляторов применяются методы синте­за цифровых САУ, основанные на псевдочастотных АФЧХ, мето­дах фильтрации, робастных методах. Усложнение САУ привело к появлению статистических методов. Строгие математические методы синтеза на основе принципа максимума Понтрягина, ди­намического программирования Беллмана и их вариации при про­ектировании САУ получили прикладное развитие за счет прибли­женных алгоритмов оптимизации.

Итак, машинно-ориентированные методы — это известные в тео­рии САУ методы, реализуемые на ЭВМ в результате составления соответствующего вычислительного алгоритма и программы.

Машинные методы — это методы, которые без ЭВМ не имеют смысла и созданы только для решения задач на ЭВМ (рис. 20, в). Это методы математического и полунатурного моделиро­вания, решения задач численного анализа, синтеза, идентифика­ции, методы расчета и машинной обработки больших массивов информации. Только благодаря машинным методам появилась реальная возможность исследовать и проектировать сложные САУ и их устройства (например, БЦВМ, регуляторы на микро­процессорах) в существующие сжатые сроки и с требуемым каче­ством. Машинные методы — новые методы в теории САУ, их исто­рия не превышает 25—30 лет.

Машинно-аналитические методы — это методы, которые вклю­чают в себя как аналитические процедуры, так и машинные чис­ленные решения и сводятся к процедурам, представленным на структурной схеме рис. 20,г. При таком подходе оказывается возможным получать в аналитическом виде математические зави­симости между характеристиками процессов в САУ и ее парамет­рами, что открывает широкие пути для дальнейших исследований И в то же время сокращает затраты машинного времени на реа­лизацию всех вариантов численного анализа при «чисто» машин­ных методах.

Алгоритмы, вытекающие из методов, частично будут изложены как компоненты соответствующих подсистем САПР в гл. 4—10, поэтому ограничимся основными правилами их построения. Алго­ритмы строятся из отдельных операторов. В соответствии с мето­дом после задания исходных данных (числовых значений, слов, знаков и т. д.) строится последовательность базовых операторов из заданного их набора. Способы реализации этих операторов считаются известными. Оператор должен быть далее неделимым элементом алгоритма. Составляется структура алгоритма, связы­вающая базовые операторы. Такую структуру обычно отобража­ют графом, вершинами которого являются операторы, а ребра­ми— связи между операторами. Различные структуры алгорит­мов, представленные соответствующими графами (рис. 20), включают последовательные (рис. 20, а), параллельные (рис. 20, б), циклические (рис. 20, в), переключающие (рис. 20, г), иерархические (рис. 20, д) и комбинированные из рассмотрен­ных структур.

В качестве операторов u_i в приведенных структурах применя­ются операторы (3.16) — (3.18), (3.27) и др., вытекающие из ММ САУ (3.7) —(3.32).

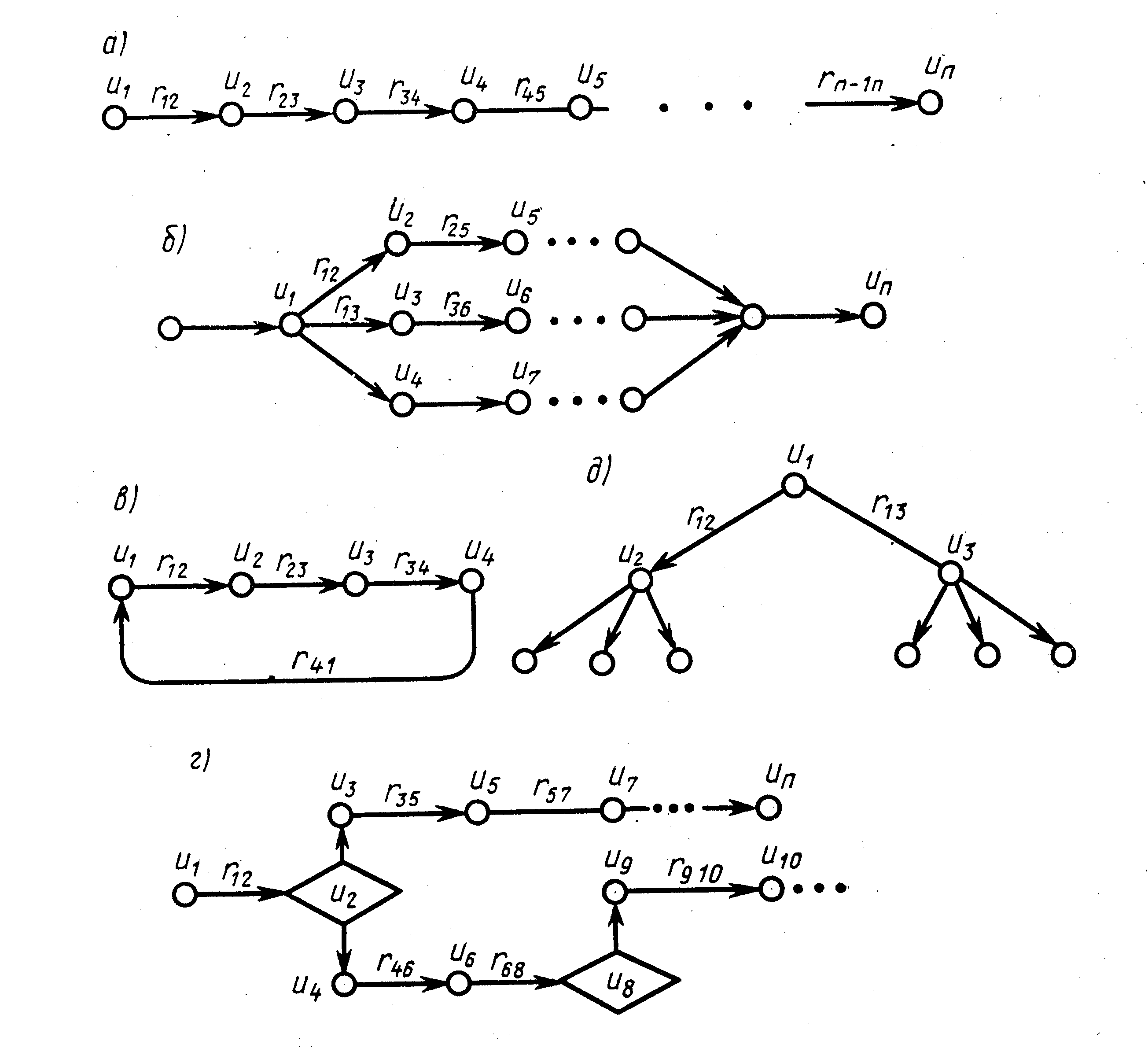
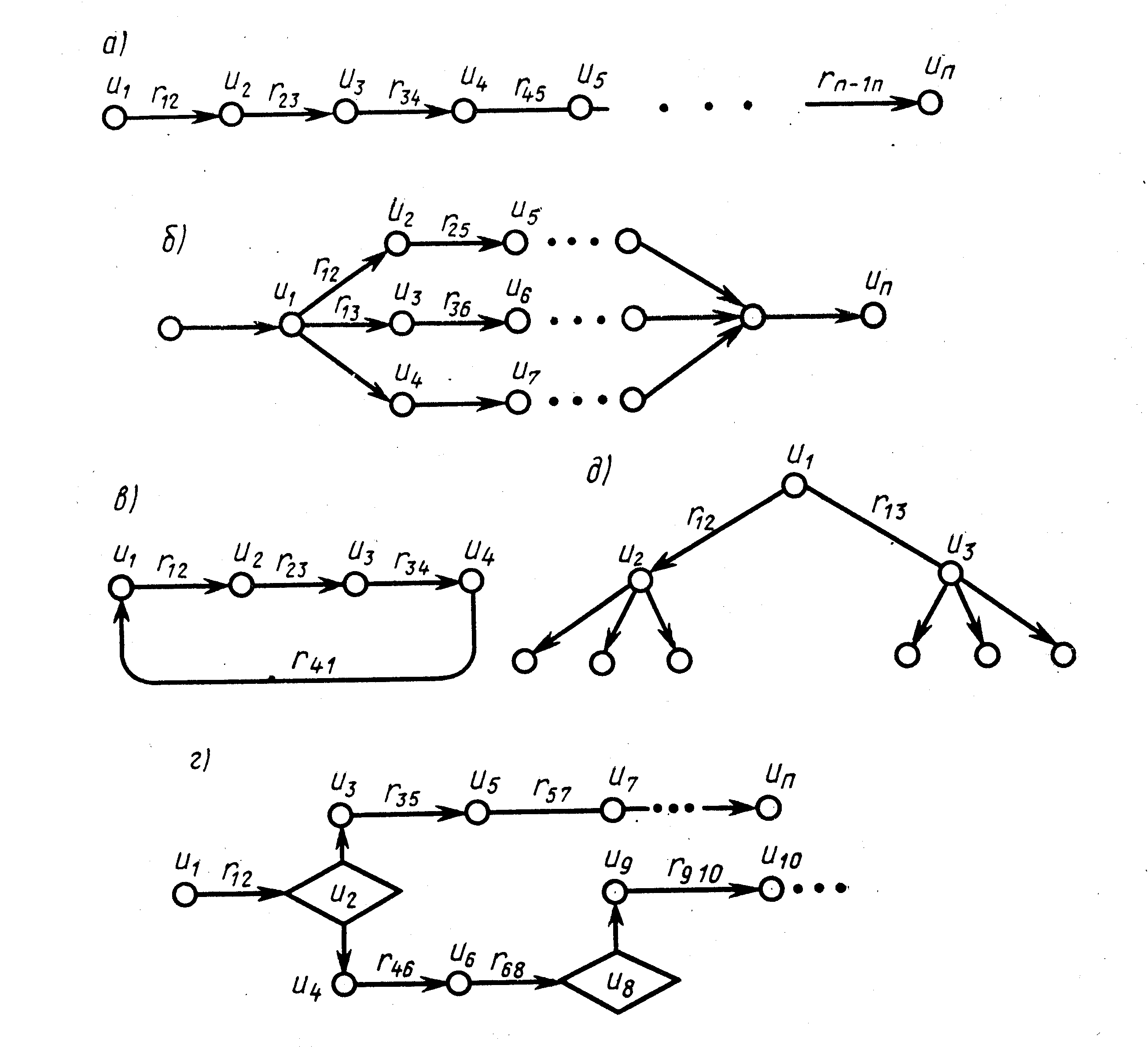
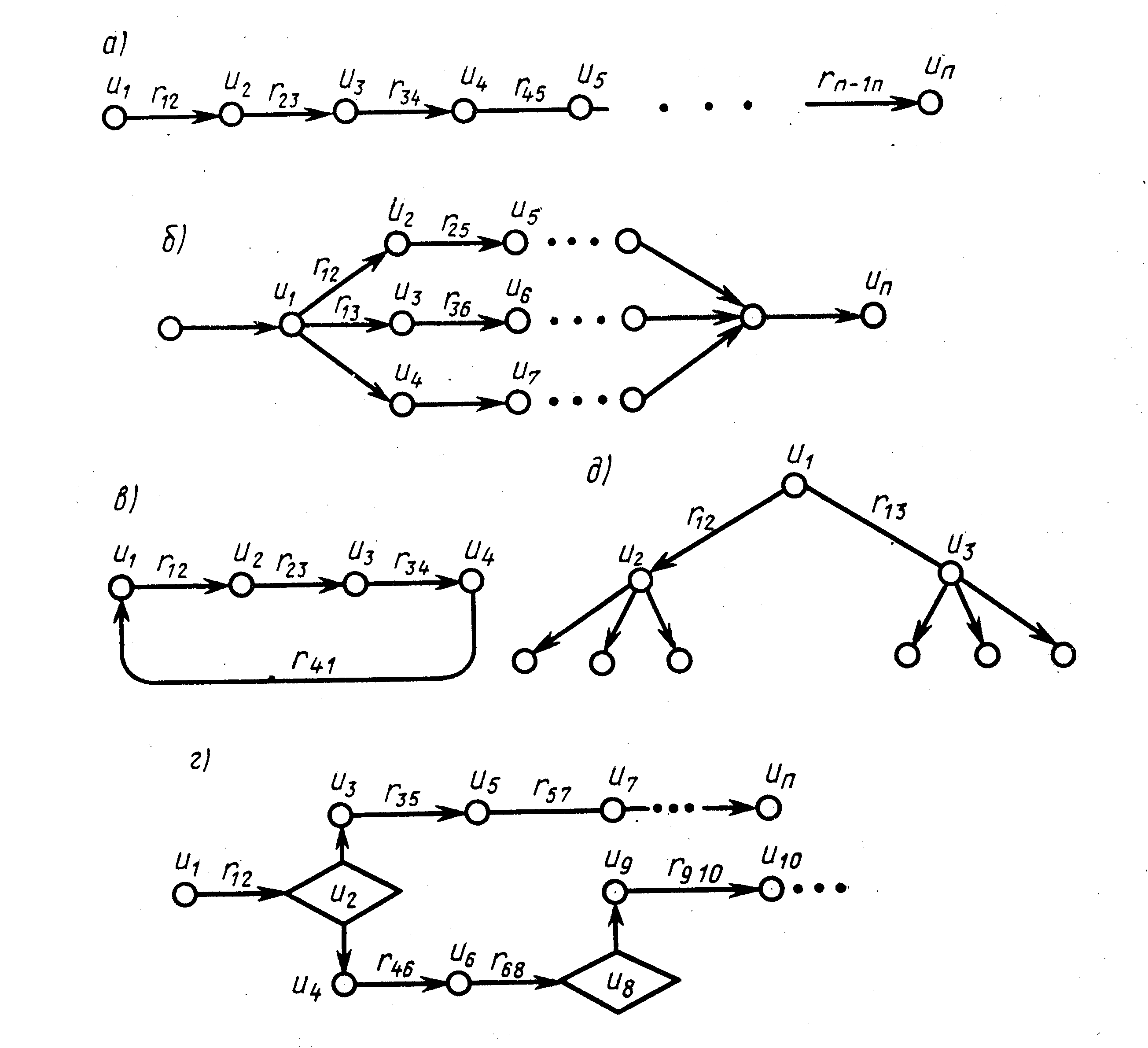
рис. 20. Структуры алгоритмов:

а – последовательная, б - параллельная, в - циклическая,

г – переключающая, д – иерархическая.