
- •Часть I р. И. Сольницев
- •Глава 1 Введение в автоматизацию проектирования систем автоматического управления
- •§ 1.1. Системы автоматического управления (сау) как объекты проектирования
- •§ 1.2. Сапр как новые средства проектирования
- •§ 1.3. Этапы истории развития сапр сау.
- •Автоматизация проектирования систем и средств управления
- •Дерево целей проектирования:
- •История развития сапр.
- •Задача векторной оптимизации.
- •Глава 2 процесс проектирования сау и его автоматизация
- •§ 2.1. Цели, критерии и условия ограничений процесса проектирования
- •§ 2.2. Этапы проектирования и проектные процедуры
- •Математическая модель Системы Проектирования (сп) как «спирали проектирования»
- •Глава 3 структура системы автоматизации проектирования сау
- •§ 3.1. Концепция, принципы и их структурная реализация
- •§ 3.2. Техническое обеспечение.
- •§ 3.3. Математическое обеспечение
- •§ 3.4. Лингвистическое обеспечение
- •§ 3.5. Программное обеспечение
- •§ 3.6. Информационное обеспечение
- •§ 3.7. Методическое и организационное обеспечение
- •Глава 4 автоматизация построения математических моделей сау
- •§ 4.1. Методы построения математических моделей и их применение в сапр
- •§ 4.2. Вывод математических моделей в аналитическом виде на эвм
- •§ 4.3. Упрощение и преобразование математических моделей на эвм
- •Математическое обеспечение сапр.
- •Стационарные линейные детерминированные модели систем с сосредоточенными параметрами.
- •Переход от дифференциальных уравнений n – ого порядка к нормальной форме Коши
- •Математические модели элементов сау.
- •Методы линеаризации уравнений
- •Глава 5 моделирование систем автоматического управления
- •§ 5.1. Методы моделирования и их применение в сапр
- •§ 5.2. Приведение математических моделей сау к виду, удобному для моделирования
- •§ 5.3. Численные методы и алгоритмы моделирования
- •§ 5.4. Контроль и оценка точности моделирования
- •Глава 6 автоматизация анализа сау
- •§ 6.1. Методы анализа сау и их применение в сапр
- •6.2§. Машинные методы анализа
- •§ 6.3. Машинно-аналитический метод анализа
- •§ 6.4. Подсистема сапр сау «Анализ»
- •Глава 7 Автоматизация синтеза сау
- •§ 7.2. Машинные методы синтеза
- •§ 7.3. Подсистема сапр сау «Синтез»
- •Методы нлп
- •Задача нлп
- •Градиентный метод оптимизации
- •Метод градиента
- •Метод случайного поиска
- •Метод Даниленко-Каган
- •Метод Трахтенбергп
- •Экстраполяционный случайный поиск с адаптирующимся шагом
- •Алгоритм с перестройкой вероятностных характеристик поиска
- •Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов
- •Локально – глобальный поиск коллективом автоматов имени Буша – Мостселлера.
- •Методика выбора алгоритмов поисковой оптимизации.
- •Метод ситуационного управления:
Метод случайного поиска
Достоинства:
Пригодность для любой функции Q(x) независимо от того, является она унимодальной или нет.
Вероятности успеха поиска оптимального решения не зависит от размерности пространства независимых переменных х.
Достаточно просто учитывает ограничение на область поиска в виде неравенств:
а)
![]()
б)
![]()
Случайный поиск с адаптацией шага
![]() (1)
(1)
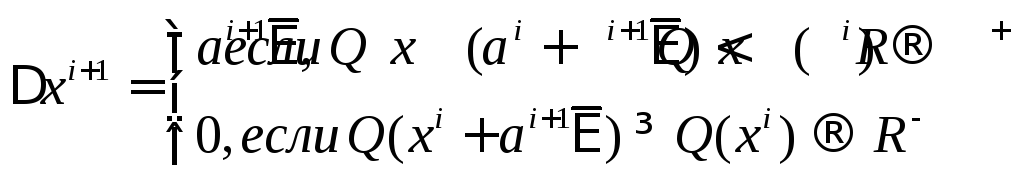
Знаки имеют место при поиске минимума
![]() –случайный вектор
–случайный вектор
![]() ,
составляющей которого являются случайные
числа, равномерно распределенные от -1
до +1
,
составляющей которого являются случайные
числа, равномерно распределенные от -1
до +1
а– рабочий шаг поиска
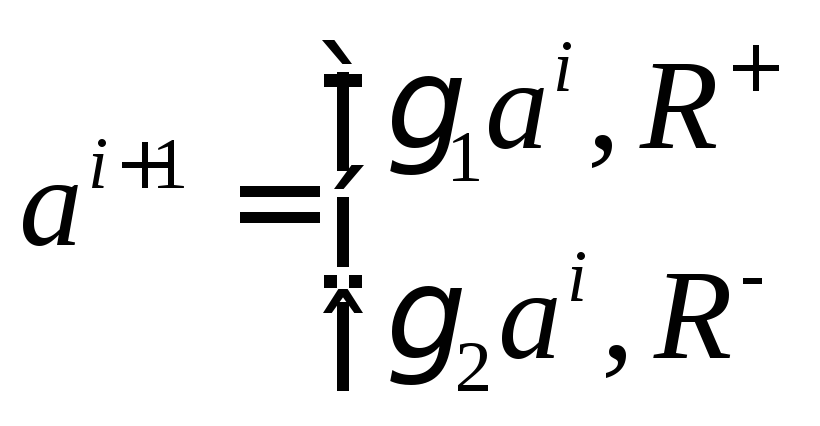
![]() - удачный шаг
- удачный шаг
![]() - неудачный шаг
- неудачный шаг
![]()
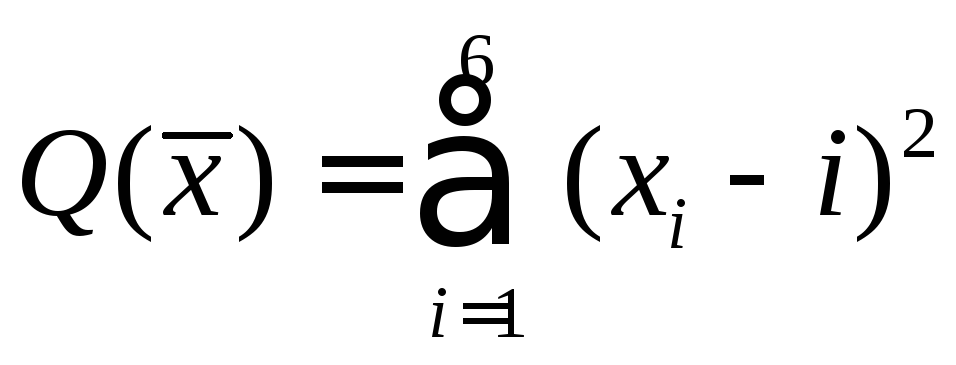 позволило определить
диапазон изменения
позволило определить
диапазон изменения
![]() и
и![]()
получили
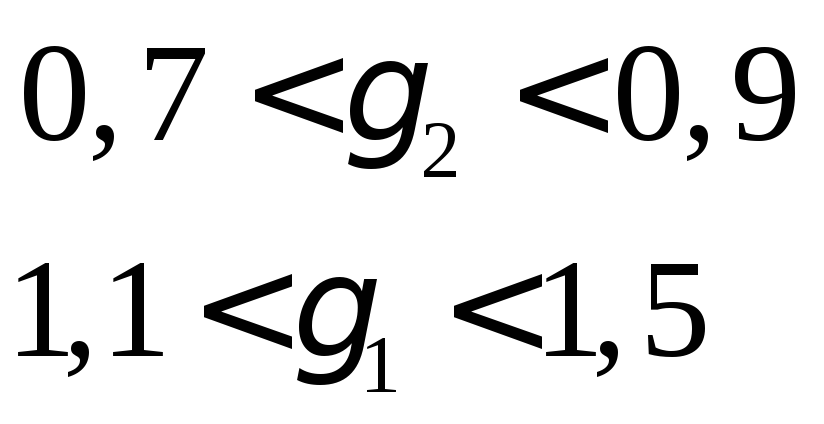
Вблизи экстремума
желательно
![]() уменьшить до 0,5.
уменьшить до 0,5.
Если
![]() ,
то система
,
то система![]()
Приблизительно
величины выбираем такими:
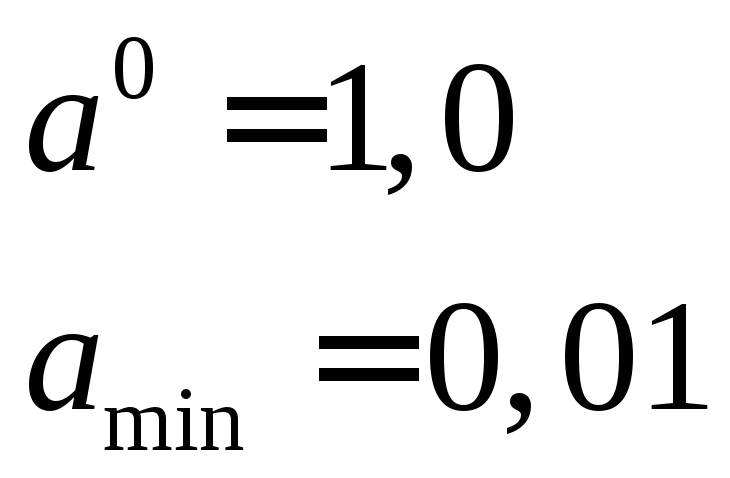
Метод Келли -Уиллинга
После того как задана начальная точка, строится случайная траектория для последовательности шагов по следующему алгоритму:
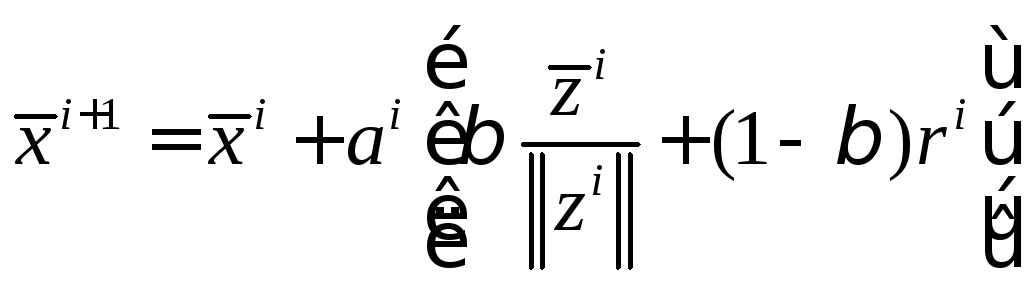
![]()
![]() -
величина шага поиска
-
величина шага поиска
![]() - вектор предыстории,
указывающий среднее направление поиска
на предыдущих шагах
- вектор предыстории,
указывающий среднее направление поиска
на предыдущих шагах
![]() - единичный вектор
отклонений , реализуемый генератором
псевдослучайных чисел по нормальному
закону
- единичный вектор
отклонений , реализуемый генератором
псевдослучайных чисел по нормальному
закону
![]() - коэффициент,
измеряемый в процессе поиска
- коэффициент,
измеряемый в процессе поиска
![]() - постоянный весовой
множитель
- постоянный весовой
множитель
![]() -
вектор масштабных множителей для
масштабирования
-
вектор масштабных множителей для
масштабирования
Случайный поиск с самообучением.
Растригин-Рипа
Алгоритм случайного поиска с непрерывным самообучением, способным настраиваться на соседние более благоприятные направления, что повышает его мобильность, по сравнению с покоординатными алгоритмами обучения.
Алгоритм записывается в виде рекуррентной формулы.
![]()
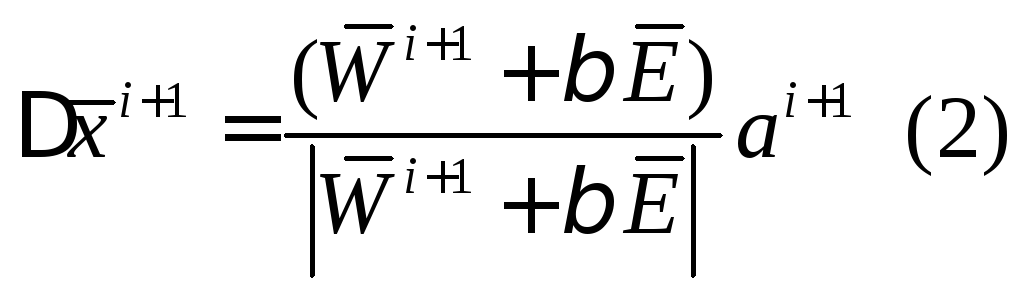
![]()
![]()
![]() - вектор
предпочтительного направления, величина
которого ограничена величиной «С»
- вектор
предпочтительного направления, величина
которого ограничена величиной «С»
![]() - смещение независимых
переменных на (i+1) шаге
- смещение независимых
переменных на (i+1) шаге
![]() -
приращение функции качества на (i+1)
шаге
-
приращение функции качества на (i+1)
шаге
![]() - величина рабочего
шага поиска
- величина рабочего
шага поиска
![]() ,
,
![]() ,
,![]() - постоянные коэффициенты
- постоянные коэффициенты
![]() - вектор случайных
чисел, равномерно распределенный от
-0,5 до +0,5
- вектор случайных
чисел, равномерно распределенный от
-0,5 до +0,5
![]() учитывает изменение
функции качества на предыдущем шаге
учитывает изменение
функции качества на предыдущем шаге
![]() -
на начальном шаге поиска оптимальные
параметры
-
на начальном шаге поиска оптимальные
параметры
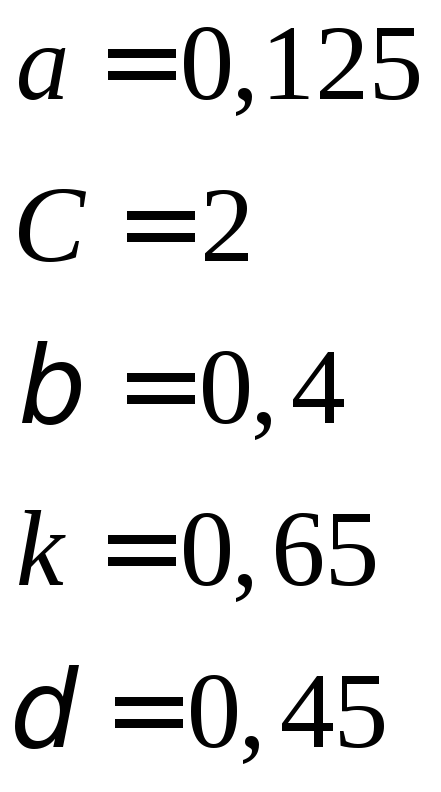
Метод Даниленко-Каган
Алгоритм реализует
пробные перемещения из точки
![]() в точку
в точку![]() по
алгоритму:
по
алгоритму:
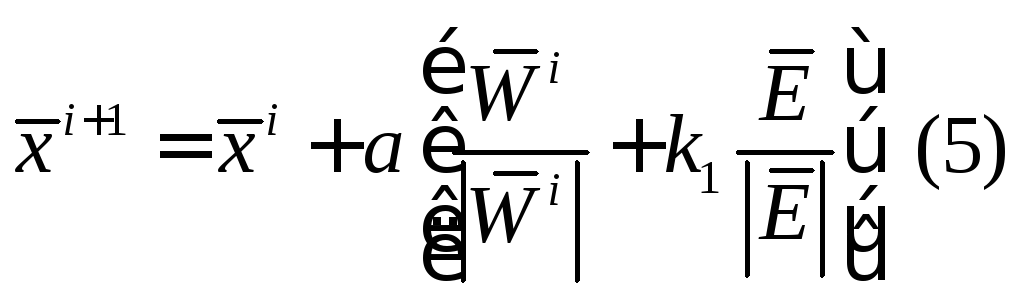
![]() - вектор случайных
чисел, равномерно распределенный от
-0,5 до +0,5
- вектор случайных
чисел, равномерно распределенный от
-0,5 до +0,5
![]() - величина рабочего
шага поиска
- величина рабочего
шага поиска
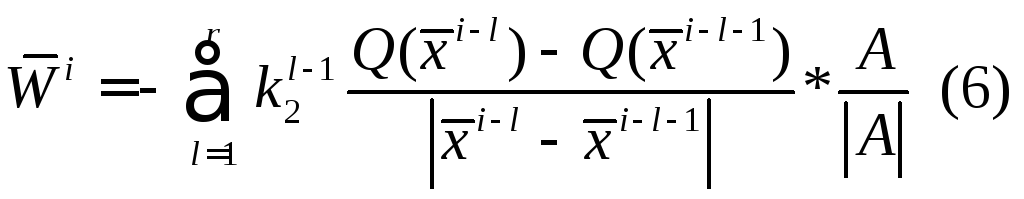
Где
![]() - коэффициент меньше 1
- коэффициент меньше 1
r- число запоминаемых предыдущих направлений
l- текущий номер запоминаемого предыдущего направления
![]() - рабочий шаг.
- рабочий шаг.
Минимальный
шаг поиска
![]()
![]() - вектор предполагаемого
направления, с каждым шагом теряет
ценность
- вектор предполагаемого
направления, с каждым шагом теряет
ценность

Метод Трахтенбергп
Алгоритм с самообучением:
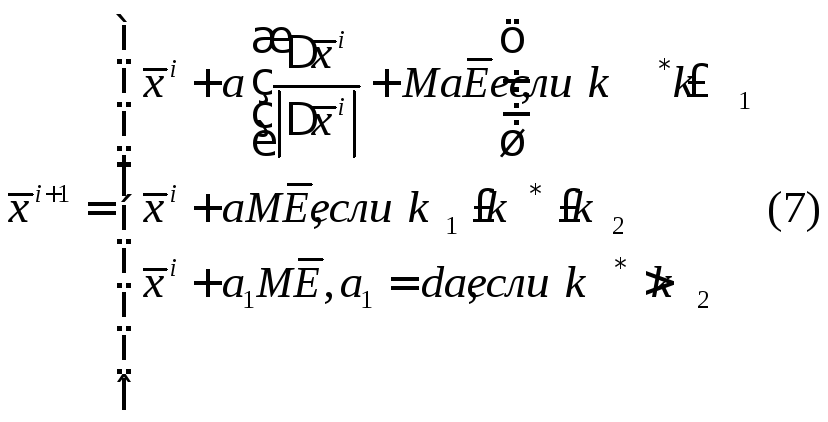
![]()
![]() - шаг поиска
- шаг поиска
M– шкальные коэффициенты (масштабные)
![]() - разница между
приращениями
- разница между
приращениями
![]() -
число, следующих подряд неудачных шагов
-
число, следующих подряд неудачных шагов
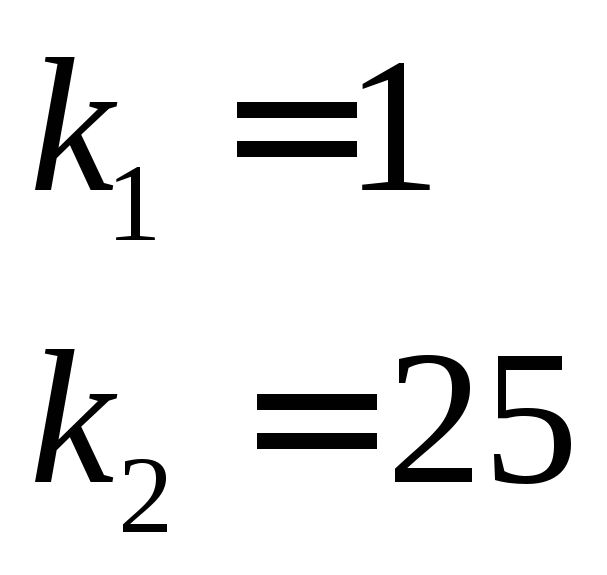
В процессе решения
задачи, значения коэффициентов
![]() ,
,![]() ,
,![]() могут быть изменены
могут быть изменены
Экстраполяционный случайный поиск с адаптирующимся шагом
Эффектом средств повышения быстродействия поиска оказывается линейная экстраполяция. Экстраполяция распространяется на случайную последовательность локальных передвижений в пространстве независимых переменных.
На i–м этапе предлагаемого метода формула экстраполяции определяется в соответствии со следующим выражением:
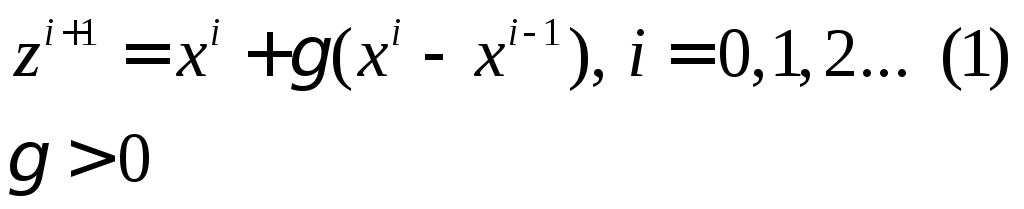
![]()
W-
некоторый метод поиска![]() без
правила остановки, состоящий изm– идентичных итераций ω; Первая из
которых действует на точку с координатами
без
правила остановки, состоящий изm– идентичных итераций ω; Первая из
которых действует на точку с координатами![]() .
На начальном этапе (i=0)
.
На начальном этапе (i=0)![]() задается
произвольно
задается
произвольно![]() .
Если точка
.
Если точка![]() удовлетворяет заданному критериюk,
то она рассматривается в качестве
исходной для итерации ω и :
удовлетворяет заданному критериюk,
то она рассматривается в качестве
исходной для итерации ω и :
![]()
В противном случае,
экстраполяция считается неудачной и
может переводится в состояние
![]() .
.
В качестве критерия допустимости экстраполяции kзадается неравенство:
![]()
В качестве итераций ω использован алгоритм случайного поиска с адаптирующим шагом, состоящий в следующем:
из
каждой точки
![]() производится
два движения:
производится
два движения: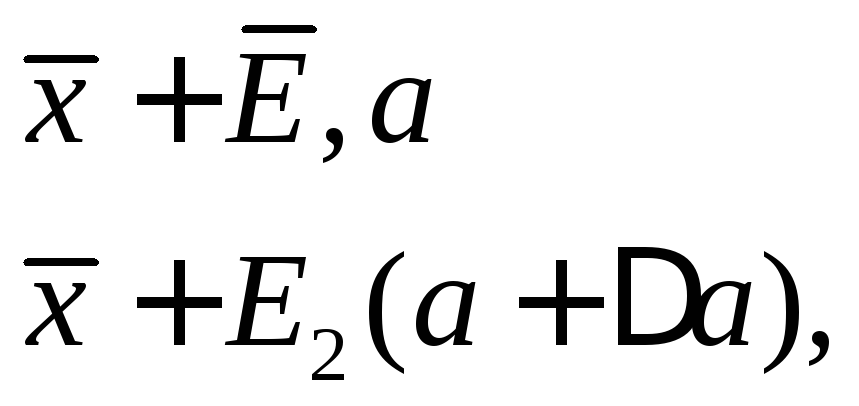
где
![]() равномерно
распределен на единичной сфере, если
на протяженииS– поток
не было ни одного удачного движения, то
величина шага уменьшается. итерация ω
считается оконченной в случае хотя бы
одного удачного движения. Конкретные
значения параметров алгоритма:
равномерно
распределен на единичной сфере, если
на протяженииS– поток
не было ни одного удачного движения, то
величина шага уменьшается. итерация ω
считается оконченной в случае хотя бы
одного удачного движения. Конкретные
значения параметров алгоритма:
![]()
Эмпирические
рекомендации по выбору
![]() алгоритм мало чувствителен к выбору
алгоритм мало чувствителен к выбору![]() вдали
от экстремума
вдали
от экстремума![]() ,
вблизи ассиметрично расположенного
экстремума следует уменьшение
,
вблизи ассиметрично расположенного
экстремума следует уменьшение![]() до 0,1. Эксперименты показывают. что
величинаSне должна
превосходитьb, а по
отношению кm>1, алгоритм
достаточно устойчив.
до 0,1. Эксперименты показывают. что
величинаSне должна
превосходитьb, а по
отношению кm>1, алгоритм
достаточно устойчив.
