Глава 4 автоматизация построения математических моделей сау

§ 4.1. Методы построения математических моделей и их применение в сапр

Под математической моделью (ММ) обычно понимается ото­бражение реального объекта с помощью системы математических соотношений.

Наибольшие трудности возникают при построении ММ объектов управления, так как учет физических процессов и явле­ний в этих объектах требует длительных и весьма трудоемких математических операций. Большое количество однообразных и утомительных операций при построении ММ, в том числе диффе­ренцирование, умножение полинома на полином, раскрытие ско­бок, приведение подобных членов, неизбежно связаны с много­численными ошибками и «ненадежностью» ММ. Автоматизация этих операций является обязательной в САПР САУ.

Будем различать графические, аналитические и численные ме­тоды построения ММ САУ.

Графические методы применяются при построении ММ САУ на верхнем уровне их описания в форме структурных схем и их графовых эквивалентов. В этом случае проектировщик исходит из представления о САУ как о сложной системе, состоящей из уст­ройств и элементов (см. структурные схемы САУ ЛА, ТГ, ГСП, ШР и их графы на рис. 18). «Внутреннее содержание» уст­ройств обычно отражается типовыми линейными звеньями САУ или условными обозначениями.

Важным условием автоматизации графических способов явля­ется разработка алгоритмов ввода структурных и графовых моде­лей в ЭВМ. Такие алгоритмы будут рассмотрены в § 4.4. Графи­ческие методы построения геометрических моделей устройств и элементов САУ широко применяются в конструкторском и техно­логическом проектировании (см. гл. 8, 9).

При аналитическом построении ММ исходными являются об­щие законы физики, результаты обобщения тысячелетнего опыта, накопленного ранее усилиями ученых и инженеров. Это прежде всего законы сохранения энергии, массы и вытекающие из них принципы наименьшего действия, непрерывности материальных потоков, кинетико-химических реакций, теплового баланса и т. п. Естественно, что приложение этих законов и принципов примени­тельно к тому или иному физическому устройству САУ приводит к различным выражениям. Так, уравнения движения объекта управления САУ ЛА как твердого тела с шестью степенями сво­боды выводятся на основе второго закона Ньютона: для поступательного движения ЛА

(4.1)

для вращательного движения ЛА относительно центра масс

(4.2)

где т(t) — масса ЛА; V(t)—вектор линейной скорости центра масс ЛА; F(t)—вектор внешних сил, действующих на ЛА; J(t), ω(t), М(t)—тензор инерции, вектора угловой скорости и момен­та внешних сил соответственно.

Уравнения движения объектов управления, устройств САУ также выводятся на основе соответствующих законов и принци­пов. В частности, уравнения движения механических и электро­механических устройств строятся с помощью формализма Лагранжа:

где Т(q_i, q_i', t)—кинетическая энергия системы, скалярная функ­ция, зависящая от координат, скоростей, моментов инерции и масс системы; q_i(t), q_i'(t)—обобщенные координаты и скорости; t — время; Q_i(t), —обобщенные силы.

Уравнения движения радиоэлектронных устройств и элемен­тов САУ выводятся на основе законов Кирхгофа I и II рода:

где I_sk, U_sк, Е_k — токи, падения напряжения и ЭДС в соответст­вующих контурах электрической схемы.

Уравнения движения гидравлических, пневматических и дру­гих устройств САУ выводятся на основе аналогичных законов.

Удобен для вывода дифференциальных уравнений движения динамической системы формализм Лагранжа (4.3). Замечатель­ное свойство формализма Лагранжа — его независимость от вы­бора обобщенных координат q_i, поэтому появляется возможность выбора удобной для исследований системы координат. Обобщен­ные силы Q_i являются производными от функций энергии различ­ного происхождения: потенциальной U(q_i) «энергии рассеяния» D энергии регуляторов Е(q_i, q_i),

т. е.

Пример 4.1. Построение ММ движения звень­ев «ноги» шагающего робота (ШР) на основе формализма Лагранжа.

Кинематическая схема в этом примере со­стоит из двух звеньев и двух шарниров (рис. 4.1). Будем считать для простоты выкладок дли­ны этих звеньев одинаковыми — l, а массы — сосредоточенными в серединах звеньев и также одинаковыми. Тогда кинетическая энергия пер­вого звена будет

где J₁ и ω₁ — момент инерции и угловая скорость вращения первого звена относительно начала ко­ординат, или

(4.8)

Аналогично, кинетическую энергию второго звена можно представить выражением

(4.9)

а полная кинетическая энергия является суммой энергий звеньев:

(4.10)

Обобщенные силы Q_i для рассматриваемой системы будут

(4.11)

Следуя формализму Лагранжа, запишем теперь выражения для соответствующих частных производных:

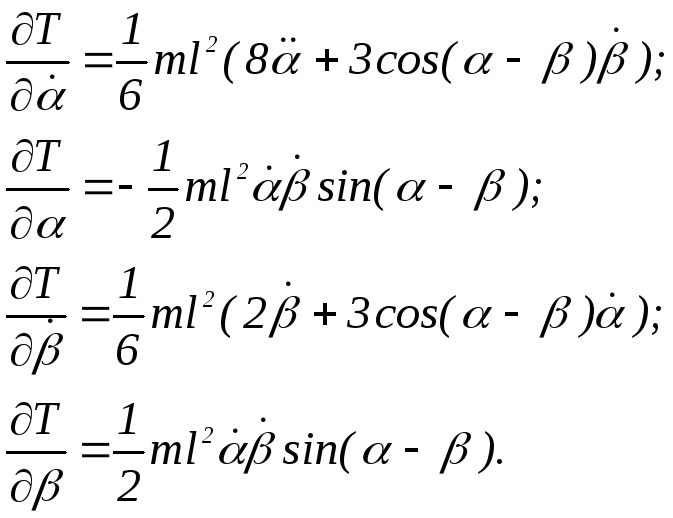(4.12)

и обыкновенных производных:

(4.13)

В результате получим выражение для ММ динамики рассматриваемой системы:

(4.14)

Численные методы формирования ММ, включают в себя по­следовательность операций по обработке и анализу априорной и апостериорной числовой информации об объекте. В результате выполнения анализа получаются структура и параметры ММ объекта.

Последовательность операций при этом обычно такая.

Задаются математические зависимости между входными и вы­ходными переменными в статике. Проводится факторный анализ априорных и апостериорных данных с целью отсеивания несуще­ственных переменных в этих зависимостях. Под факторным ана­лизом, понимается приближенная оценка параметров и коэффици­ентов уравнений в зависимости от выбранной меры точности сов­падения экспериментальных и теоретических данных.

Проводятся эксперименты по определению реакции системы на воздействия по времени. Строятся оценки динамических ха­рактеристик объекта во времени. Строятся математические зави­симости между выходными и входными переменными в динамике.

Перечисленные операции методики построения ММ входят как составляющие в большой раздел теории САУ, известный как идентификация систем и устройств.

Под идентификацией в теории САУ обычно понимают построе­ние ММ объектов по априорной и апостериорной информации и, в частности, по известным их входным и выходным сигналам. Наиболее распространены методы параметрической идентифика­ции, когда структура ММ уже задана, а требуется найти только ее параметры в соответствии с заданными критериями адекват­ности ММ и объекта.

Вопросам идентификации в настоящее время уделяется боль­шое внимание. На базе многочисленных исследований, статей, книг, а также работы конгрессов ИФАК начиная с 1967 г. осу­ществлялось становление идентификации как важного раздела технической кибернетики.

Определение ММ динамики системы сводится к идентификации оператора L в выражении

(4.15)

где Y=(y₁,y₂ … y_n), Х=(x₁, x₂ ..., х_l) —векторы выходных и входных сигналов САУ;Λ— (λ₁, λ₂…,λ_т) —вектор параметров системы; С=(с₁ с₂, ..., с_r)—вектор сигналов помех, возникающих внутри системы; L — искомый оператор, в общем случае нели­нейный.

Применяемые на практике методы идентификации разработа­ны в основном для линейных детерминированных и стационарных стохастических систем. В последнем общем случае большое чис­ло этих методов базируется на известном уравнении Н. Винера (американский математик и кибернетик, 1894—1964), выведенном для определения характеристик фильтров:

(4.16)

где h(τ) — неизвестная весовая вектор-функция системы; К_хх(τ) — известная корреляционная матрица; К_xу(τ)—взаимно корреляци­онная вектор-функция стационарных случайных процессов на вхо­де и выходе этой системы.

Наиболее плодотворными и перспективными являются методы идентификации оператора L, построенные на принципе настраи­ваемой модели. Основная идея этого подхода сводится к схеме, представленной на рис. 4.2. Эта общая схема включает в себя довольно широкий набор вариантов, которые различаются в ос­новном организацией процесса настройки модели в смысле приня­того критерия идентификации. Выбор такого критерия — сложная задача, во многом определяющая алгоритмы и техническую реа­лизацию подобных схем.

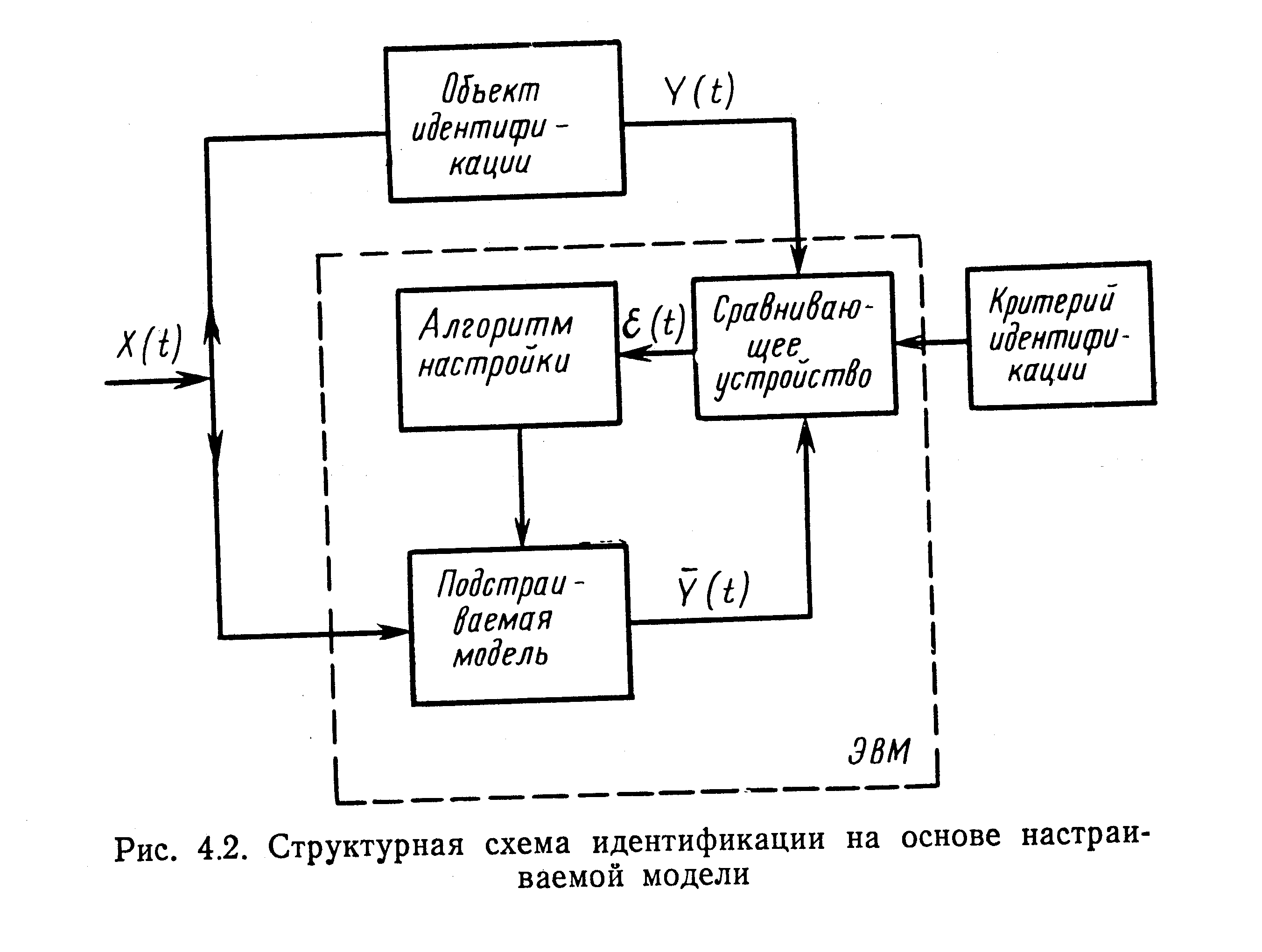
Наиболее распространены выражения критериев в виде функ­ционалов: интеграл квадрата ошибки ε(t)=Y(t)—Y'(t)

(4.17)

интеграл от ошибки с весовой функцией времени

(4.18)

выделяющий ошибку тем больше, чем позже она появилась по отношению к входному сигналу; интегральный критерий вида

(4.19)

который позволяет осуществлять нормированную по входному сигналу х(t) оценку ошибки ε(t).

В последнее время в качестве критериев идентификации ис­пользуются получившие распространение в теории оптимальных систем функции потерь или штрафа, под которыми в идентифика­ции понимается штраф, связанный с недостижением абсолютно точной идентификации. В общем виде этот критерий представля­ют в виде условного математического ожидания штрафа за ошибку:

(4.20)

где G[ε(t)] означает штраф за ошибку ε(t)=Y(t)—Y'(t); Y — истин­ное значение вектора выходных координат; Y'(t)—оценка Y, осно­ванная на некотором его наблюдении; p(ε / Y) —условная плот­ность вероятности величин ε и Y.

В схемах с настраиваемой моделью, как правило, структура модели предполагается известной, а настройке подвергаются па­раметры модели. Наиболее распространенными алгоритмами на­стройки являются градиентные и итерационные. Применение су­ществующих методов идентификации к САУ приводит к необхо­димости решения сложных алгоритмических и вычислительных задач в связи с гетерогенностью, большой неопределенностью, многосвязностью САУ.

Наиболее целесообразным способом построения ММ САУ, ко­торый можно положить в основу построения соответствующей подсистемы САПР САУ, является сочетание аналитических мето­дов с численными. При этом аналитическими методами строятся возможно более полные ММ, а с помощью численных методов идентификации осуществляется количественная оценка парамет­ров модели и обеспечивается адекватность ее реальному объекту. Такой подход, реализуемый средствами САПР, оказывается эф­фективным не только для экономии высококвалифицированного труда, но и для значительного повышения адекватности ММ САУ реальному объекту. При этом процедура построения ММ состоит из трех этапов:

— вывод полной ММ в аналитической форме на основе клас­сических принципов и формализмов динамики;

— упрощение и преобразование ММ в соответствии с назначе­нием и особенностью модели;

— параметрическая идентификация упрощенных ММ по ре­зультатам экспериментальных исследований и испытаний.

В последующих параграфах рассматриваются вопросы авто­матизации первого и второго этапов построения ММ САУ. Авто­матизация третьего этапа будет показана в гл. 10 с помощью средств подсистемы «Испытания» САПР САУ.