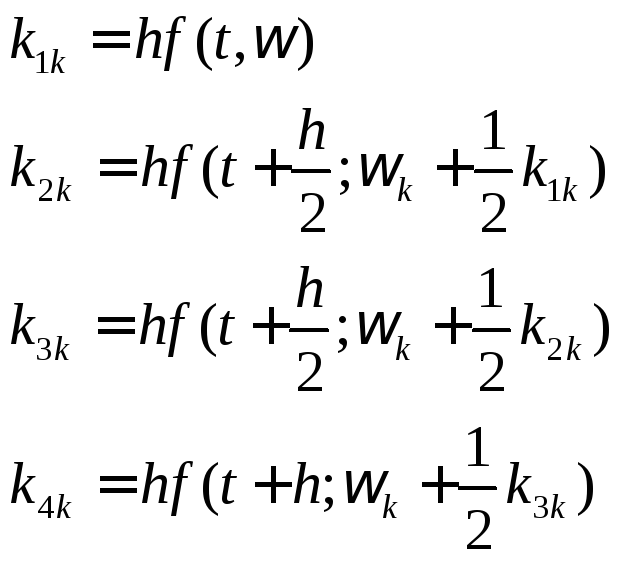Математические модели элементов сау.

Математические модели элементов САУ составляются в виде алгебраических, дифференциальных, дифференциально-интегральных, конечно-разностных уравнений. Описание процессов в элементах с сосредоточенными параметрами используют обыкновенные дифференциальные уравнения, а в системах с распределенными параметрами – уравнения в частных производных.

При проектировании САУ нелинейные уравнения обычно линеаризуют и приводят к векторно-матричной форме, либо к частотным функциям.

В тех случаях, когда рассматриваемые процессы в элементах не удается описать указанным выше способом, используют таблицы с числовыми значениями, характеризующие входные и выходные переменные. Применение к ним метода регрессионного анализа, основанного на методе наименьших квадратов, позволяет получить нелинейные, дифференциальные алгебраические уравнения.

Динамические элементы относятся к непрерывным, если рассматриваемые в них процессы и сигналы непрерывны. В этом случае, если входной сигнал и процесс на выходе имеет конечное число значений во времени, то имеем дело с дискретными элементами.

Непрерывные процессы описываются уравнением:

(1)

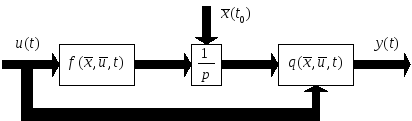
где – управляющее воздействие

- выходное воздействие

Стрелки толстые – многомерная система

Будем считать систему (1) нелинейной, если присутствующие в ней переменные состояния возводятся в степень или входят под знак радикала.

Во многих элементах нелинейности нельзя выразить в аналитической форме, тогда ее представляют графиками, либо в виде таблиц.

Пример 1. Уравнение устройства для замера угловых скоростей выходного вала ДВС или турбины.

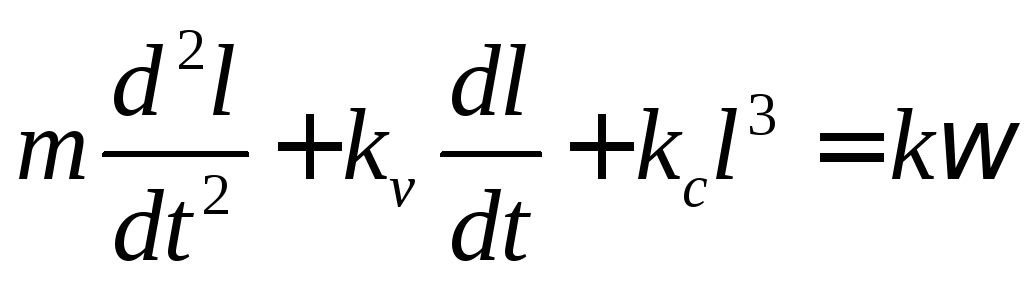
m- масса грузиков и приведенных длин рычагов

l- линейное перемещение

к_с- коэффициент жесткости пружины

к - коэффициент пропорциональности угловой скорости ДВС

к_v– коэффициент скоростного трения

к_с =

если обозначить:

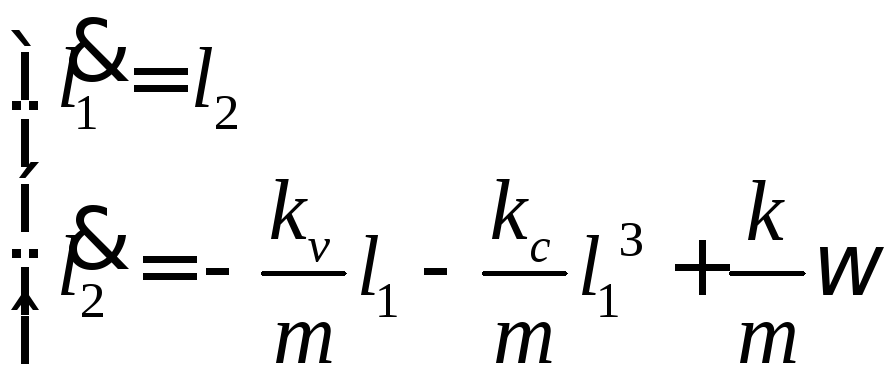
Пример 2

Объект регулирование – электродвигатель переменного тока

Уравнение вращения:

- угловая скорость вращения

I- момент инерции

K_v - коэффициент скоростного трения

K_g - коэффициент нелинейности механической характеристики двигателя

K_T- коэффициент сухого трения

K_u - коэффициент передачи электрического двигателя

-K_T < M_T < K_T

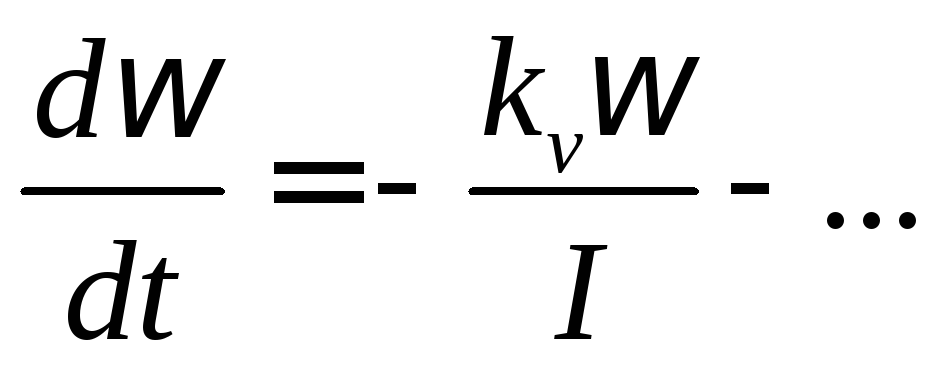
Алгоритм линеаризации исходных нелинейных уравнений в аналитической форме возможен в простейших случаях.

При описании элементов дискретного действия в общем виде пользуются разностными уравнениями.

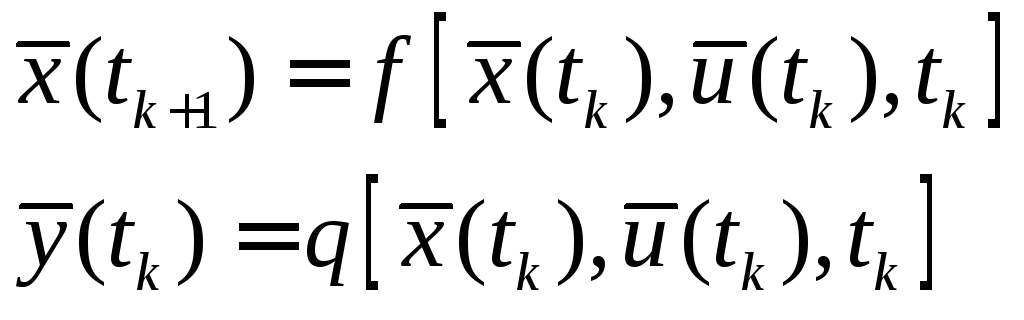(5)

Наибольшее распространение получил случай, когда шаг квантования постоянный и равен Т₀.

В этом случае систему уравнения (5) перепишем:

(6)

В дискретных системах или элементах наряду с нелинейностями. описанными выше, могут содержаться нелинейные модуляторы, ярким примером являются элементы осуществляющие квантование во времени. Обычно модуляторы представлены в виде идеального импульсного элемента, совокупность -функции, формирователь, на выходе которого получаем импульсы, с которыми имеем дело. Эти импульсы эквивалентны замене прямоугольного импульса (для случая экстраполятора первого порядка), второго порядка (где имеем максимальное приближение).

Пример 3.Опишем процессы, происходящие в элементе вал - цифра.

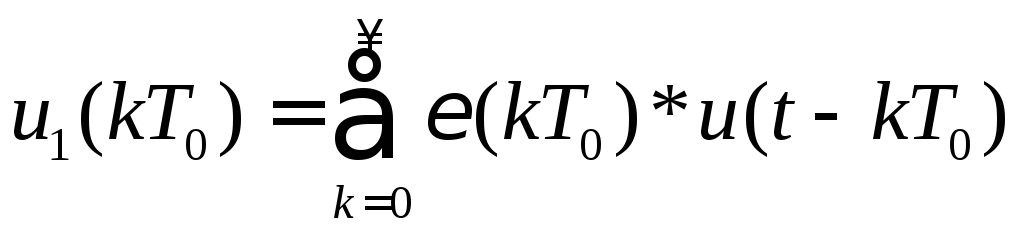
- выходная величина (сигнал)

- входной сигнал

- -функция

Если произвести гармоническую либо статистическую линеаризацию, то получим добавление коэффициента

Пример 4.Рассмотрим реализацию на ЦВМ. Систему уравнений в отклонениях от заданных траекторий полета космического аппарата, представленного в виде:

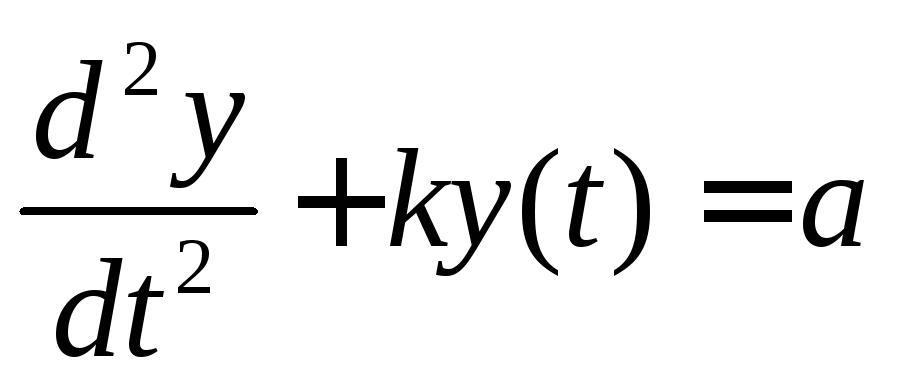(8)

y- вектор отклонения от заданной траектории

к - постоянный параметр

- ускорение, измеренное акселератором на гироплатформе летательного аппарата

Уравнение (8) является линейным и его решение на ЦВМ реализуется с помощью метода Рунге – Кутта четвертого порядка.
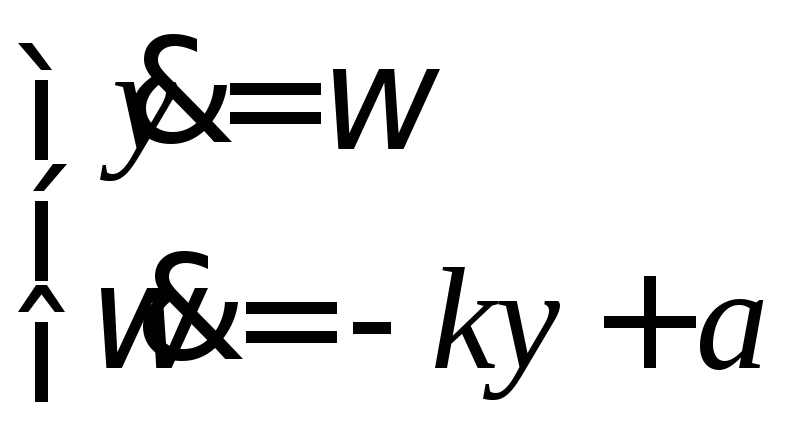