§ 6.4. Подсистема сапр сау «Анализ»

Состав компонентов инструмента разработчика САУ «Анализ» строится аналогично рассмотренным подсистемам САПР САУ «По­строение ММ» и «Моделирование». Подсистема «Анализ» взаимо­действует с остальными подсистемами САПР САУ через програм­му ИНИЦИАТОР системной части ППО (см. § 3.5, рис. 3.14), так же как и все остальные подсистемы. Компоненты математиче­ского обеспечения строятся на методах и алгоритмах анализа, рас­смотренных в § 6.1—6.3. Лингвистические компоненты включают в себя ПОЯ «Анализа САУ» и соответствующий язык программи­рования.

Взаимодействие программных модулей в составе общей струк­туры подсистемы представлено на рис. 6.8. В частности, комплекс программных модулей, осуществляющих статистическую обработ­ку временных процессов в подсистеме «Анализ», представлен на рис. 6.9. На рисунке обозначены НСП — нестационарный случай­ный процесс, ССП — стационарный случайный процесс. Структур­но этот комплекс программ можно разбить на следующие части:

2—7 — модули обработки нестационарных и стационарных слу­чайных процессов, реализующих основные расчетные алгоритмы (6.26) — (6.32) по получению оценок статистических характеристик;

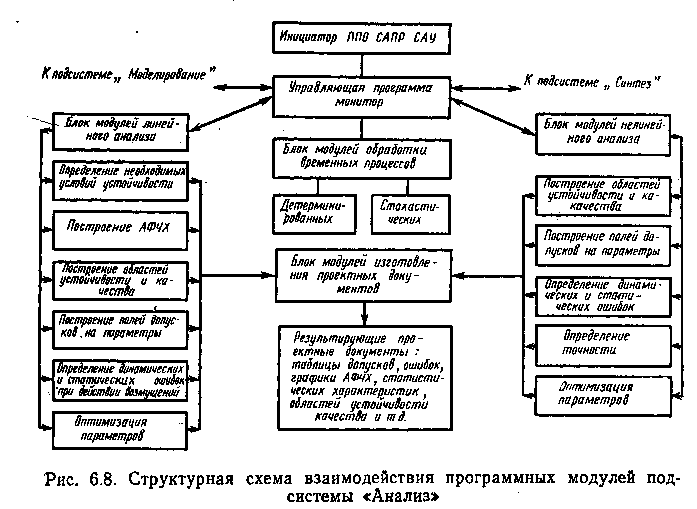
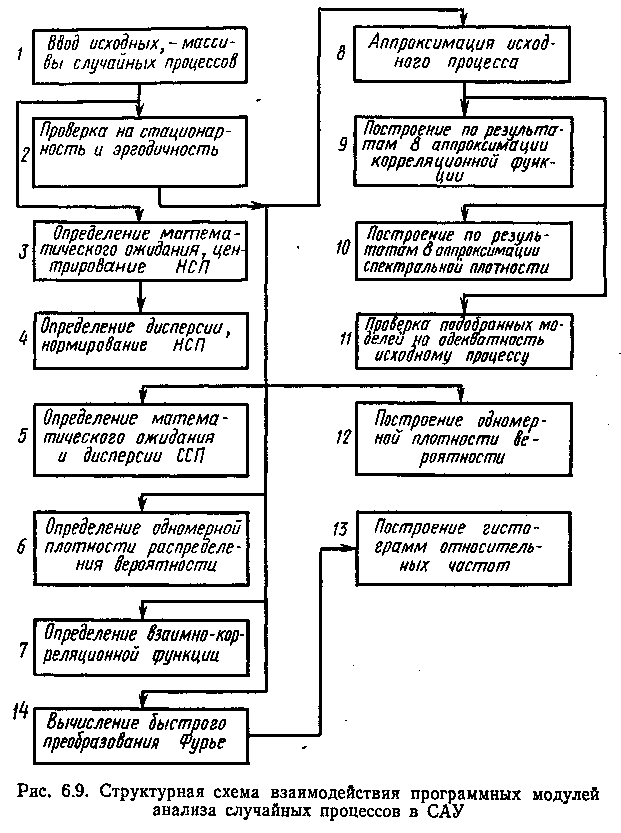
13, 14 — вспомогательные модули, такие, как быстрое преобра­зование Фурье;

8—12 — модули аппроксимации стационарных случайных про­цессов.

Входными данными для работы этого программного комплекса являются массивы значений случайных процессов, заданные в виде таблицы, размерность массивов и период дискретизации во вре­мени (предполагается, что дискретизация произведена с выпол­нением условия теоремы Котельникова).

Глава 7 Автоматизация синтеза сау

 7.1. Методы синтеза САУ и их применение в САПР

Под синтезом в научных исследованиях и проектировании обычно понимают решение задач, обратных анализу: определение структуры и параметров системы или процесса в соответствии с заданными критериями качества и условиями функционирования.

Задачи синтеза являются важнейшими и в то же время наибо­лее сложными при проектировании различных систем и процессов. Как уже отмечалось в предыдущей главе, некоторые задачи син­теза могут быть решены методами анализа. Более того, опытный инженер-проектировщик часто находит вполне пригодные струк­туру и параметры САУ на основе приближенных расчетов и эв­ристических методов. Однако трудоемкость такого синтеза оказы­вается весьма значительной. Так, надо осуществить до нескольких сотен вариантов анализа при выборе корректирующего звена САУ ТГ или параметров САР ГСП и т. д. Полученные проектные ре­шения требуется «доводить» на последующих этапах проектиро­вания, возможны и принципиальные ошибки в проектных решени­ях. При синтезе структуры и параметров САУ, как правило, не учитываются конструкторские и технологические особенности реа­лизации отдельных устройств и элементов САУ и особенно сты­ковки их между собой. Например, корректирующее звено с пере­даточной функцией

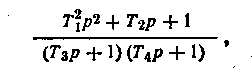
полученное методами традиционного синтеза, может оказаться нереализуемым (в частности, на пассивных или активных фильт­рах), если не удается обеспечить требуемого соотношения между постоянными времени Т₁, Т₂,T₃, T₄ в условиях конструктивных и технологических ограничений.

Прямая реализация теоретических и инженерных методов син­теза, не ориентированных на ЭВМ, часто оказывается невозмож­ной из-за быстрого исчерпывания возможностей ЭВМ по быстро­действию и оперативной памяти, неустойчивости вычислительного процесса, накопления методических и трансформированных оши­бок, сложности логических операторов и т. д. Поэтому для при­менения традиционных методов синтеза в САПР требуется их машинная ориентация. Определяющим условием правильной по­становки задачи синтеза и построения соответствующего инстру­мента САПР является формализация целей, критериев и ограни­чений. Критерии и ограничения при проектировании САУ много­численны и противоречивы, существенно зависят от типа САУ и условий их эксплуатации. Отмеченное обстоятельство иллюстриру­ется (см. § 2.1) составом целей и критериев, содержащихся в ТЗ на САУ. Критерии, принимаемые при проектировании САУ, мож­но представить следующими векторами:

Компоненты этих векторов отражают соответствующие состав­ляющие, имеющие естественное физическое содержание: k₁..., k_n1 — запасы устойчивости, время переходного процесса, динамические и статические ошибки, колебательность, оценки эффективности; M₁...,M_n2 — мощность, потребляемая устройствами САУ, рассеивае­мая энергия, энергетические ресурсы источников питания; в₁ ..., в_n3— вес отдельных устройств и элементов САУ; г₁,..., г_n4 — — габариты отдельных устройств и элементов САУ; н₁..., н_n5 — среднее время между отказами, восстанавливаемость, показатели старения САУ, ее устройств и элементов; р₁,...,р_пб— ремонтопри­годность устройств и элементов, восстанавливаемость, доступность при ремонте; с₁..., с_n7— стоимость отдельных устройств и эле­ментов и всей системы.

В § 2.1 приведены и другие критерии, но даже перечисленные показывают, насколько сложна задача их объединения в единую математическую форму — функционал, причем такой функционал должен связывать структуру и параметры САУ с целями их про­ектирования. Поэтому часто поступают следующим образом: выделяют главные критерии и второстепенные. По главным отыски­ваются экстремальные значения, а на второстепенные накладыва­ют ограничения. В частности, условия

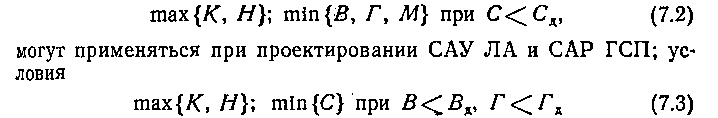
применяются при проектировании САУ ТГ.

Попытки формулирования обобщенного функционала цели про­ектирования САУ в виде линейной формы

оказываются несостоятельными ввиду практической неразреши­мости задачи оптимального выбора весовых коэффициентов а*. Не меньшие затруднения возникают и для нелинейных функционал вида

В тех случаях, когда удается связать некоторые из критериев С, К, Н, М, В, Г, P со структурой и параметрами САУ, задачи синтеза САУ сводятся обычно к задаче нелинейного программи­рования (в частном случае — линейного программирования).

Если же при решении этой задачи приходится интегрировать дифференциальные уравнения, то возникает задача вариационного исчисления и ее развития в виде принципа максимума Л. С. Понтрягина, метода динамического программирования Р. Беллмана. В некоторых случаях в виде функционала цели системы принима­ют вероятность выполнения условий

Этот функционал зависит от случайных функций и случайных ве­личин. Функционал (7.6) в отличие от (7.4), (7.5) имеет физиче­ский смысл, но вычисление его — исключительно тяжелая задача, посильная только при наличии специальных средств САПР САУ. В частности, для синтеза САУ ЛА функционал (7.6) означает синтез такой САУ, где достигалась бы наибольшая вероятность max {P} удовлетворения всех заданных требований: запасы устой­чивости, качество регулирования движения ЛА вокруг центра масс и относительно траектории, точность полета по программе, мини­мальные все и габариты, минимальный расход горючего,..., ре­монтопригодность БЦВМ и т. д.

В некоторых случаях помимо функционалов (7.4), (7.5) и (7.6) используются функционалы типа функций «потерь» или «штра­фов». Наиболее распространенная форма представления этого критерия — это условное математическое ожидание штрафа за ошибку:

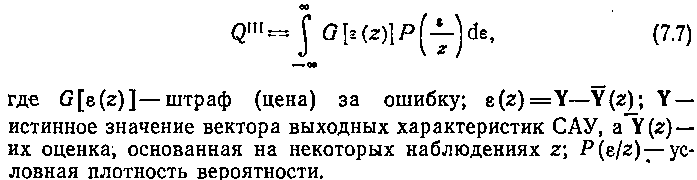
Переход от обобщенных функционалов (7.4) — (7.7) к частным вида (7.2), (7.3) осуществляется в зависимости от типа САУ и конкретной задачи синтеза. Так, далеко не полный учет требова­ний, предъявляемых только к системе стабилизации ГСП (см. § 2.2, рис. 2.8), приводит к следующим критериям и ограниче­ниям, накладываемым на углы стабилизации а_i-, углы прецессии β_i, моменты разгрузочных двигателей M_сτi время переходного процесса t_П.П. управляющий двигателем сигнал δ (t):

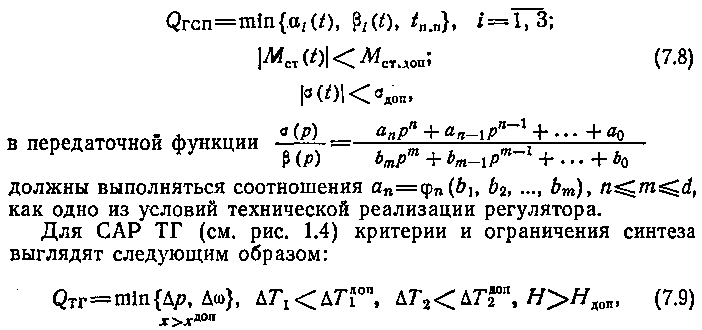
где Δр — ошибка стабилизации давления газа; Δω — ошибка ста­билизации частоты вращения турбины; ΔT₁^доп, ΔT₂^доп — ограниче­ния на допуск по температуре продуктов сгорания ТГ; Н_доп — ог­раничения по надежности ТГ.

Критерии синтеза (7.8), (7.9) представляют также в форме ин­тегральных критериев качества А.А. Фельдбаума (6.24).

При реализации традиционных методов синтеза в САПР САУ к ним предъявляются следующие требования: устойчивость и ско­рость вычислений на ЭВМ; методологические удобства применения методов в соответствии с общей идеологией САПР САУ; до­статочная близость или хотя бы непротиворечивость критериев синтеза по отношению к критериям, применяемым разработчика­ми САУ.

Деление на алгебраические, частотные и корневые методы син­теза сохраняется в том же виде, что и при анализе САУ. Однако содержание и направленность их принципиально иные. Если при анализе требовались оценки устойчивости, качества, точности, то при синтезе необходимо найти структуру и параметры в основном изменяемой части САУ, обеспечивающие заданные, критерии по устойчивости, качеству и точности.

Алгебраические методы синтеза для одномерной САУ строятся на определении вида и параметров передаточной функции изменя­емой части САУ в выражении

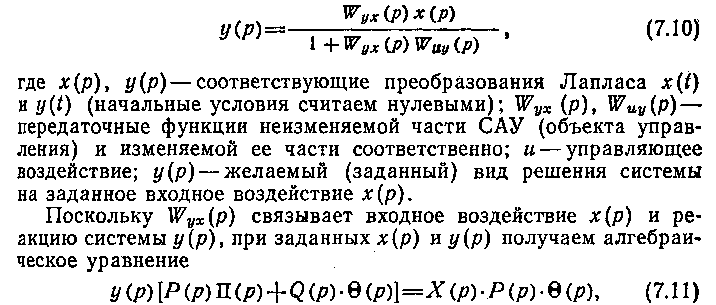
Рассмотренный подход развит в виде метода полиноми­альных уравнений, который может быть применен как к непрерывным, так и к цифровым регуляторам САУ. В последнем случае этот метод наиболее эффективен. По существу он является численным методом решения определенного круга вариационных задач и позволяет единообразным путем, учтя условия физической реализуемости и устойчивости САУ, получить в явной форме вы­ражение оптимальной передаточной функции регулятора W_uy. Важным достоинством метода является то, что оптимальность здесь понимается не только в смысле быстродействия, но и в смысле компенсации нежелательных отклонений САУ от заданно­го движения, что приближает задачу синтеза к инженерной поста­новке в смысле критериев (7.8) — (7.9).

Применение метода полиномиальных уравнений требует пере­хода к «дискретной модели» непрерывной части системы, т. е. представления (3.15)) в формах (3.26), (3.27).

Для удобства последующего изложения рассмотрим алгоритм метода применительно к одномерной системе (7.10). Осуществляя преобразование функции (7.10), представим ее в виде

Тогда y(t) будет процессом конечной минимальной длительности при возможности одновременного обеспечения устойчивости и ми­нимума динамической ошибки. Подставляя найденные П и Θ в (7.17), находим искомую функцию W_uy(z).

При использовании наряду с принятыми дополнительных кри­териев синтеза, например минимальной суммарной квадратичной ошибки, как ^ выражение (7.17), так и полиномиальное уравнение (7.19) могут значительно усложняться, что, однако, не носит прин­ципиального характера. Метод позволяет весьма точно учитывать ограничения со стороны неизменяемой части системы, путем при­влечения аппарата линейного программирования. Задачи стати­стического синтеза также сводятся к решению систем полиноми­альных уравнений. Применительно к задачам синтеза регуляторов САУ метод полиномиальных уравнений имеет ряд преимуществ: простоту машинной ориентации метода, практическое отсутствие вычислительных трудностей и возможность синтеза систем, обла­дающих свойством удовлетворять совокупности различных требо­ваний (достигается абсолютный экстремум по одному из крите­риев при относительных экстремумах по остальным). Результатом синтеза является передаточная г-функция или эквивалентное раз­ностное уравнение, реализуемые в дальнейшем на микропроцес­соре САУ.

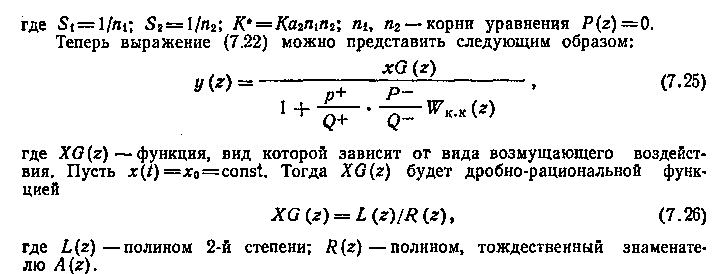
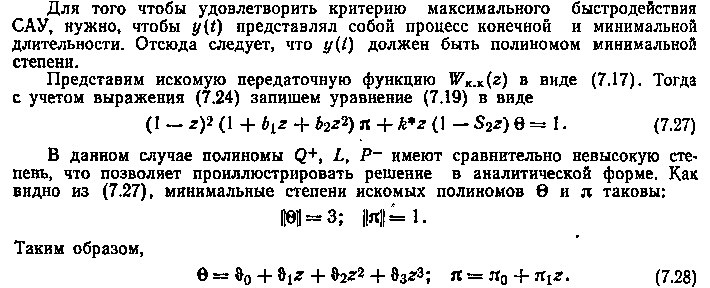
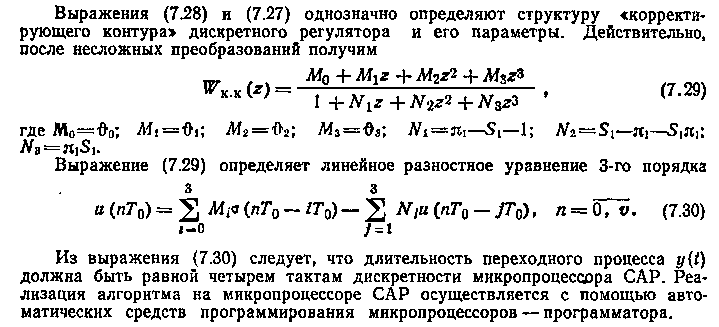
Частотные методы синтеза САУ строятся на основе критериев качества, связанных с ЧХ: запасы устойчивости по фазе (φ) и по амплитуде (L), показатель колебательности (М), частота среза разомкнутой системы (ω_ср) при учете ограничений на величины динамической (Y_дин) и статической ошибок (Y_ст), обусловленных типовыми воздействиями.

Системы регулирования считаются приемлемыми, если выпол­няются неравенства

В простейшем случае такая задача решается путем машинной ориентации метода АФЧХ. В качестве исходных данных задается исходная структурная схема САУ, свойства которой не удовлетво­ряют критериям (7.31).

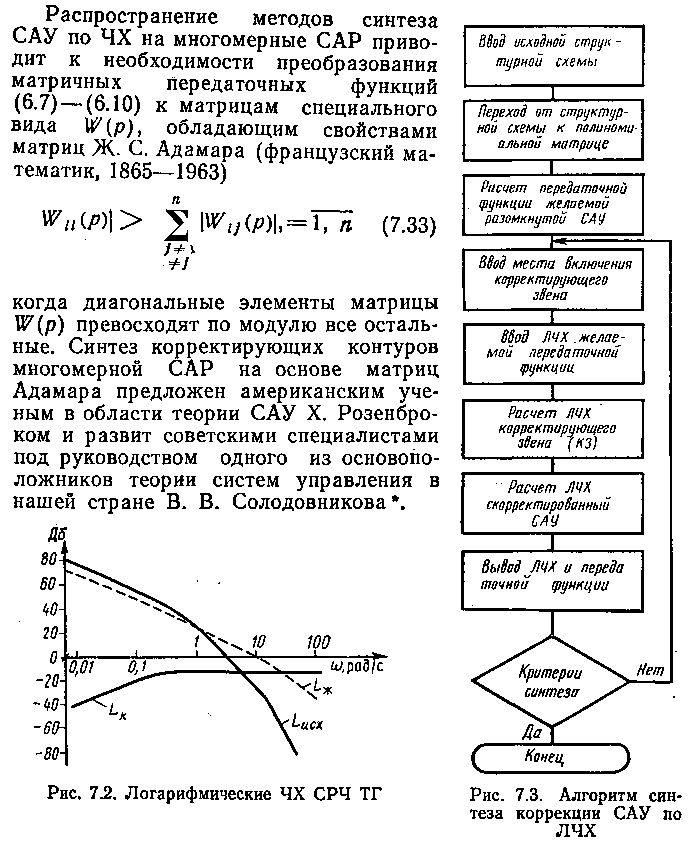
На структурной схеме выделяются точки возможного съема и ввода сигналов коррекции, т. е. задается множество возможных мест включения коррекции. По заданным требованиям к дина­мике системы в соответствии с какой-либо из известных методик частотного синтеза формируются асимптотические логарифмиче­ские ЧХ(ЛЧХ) нескольких разомкнутых желаемых САУ, которые должны быть согласованы с ЛЧХ исходной разомкнутой системы и могут отличаться некоторыми параметрами. Автоматизация про­цедуры синтеза состоит в получении передаточной функции кор­ректирующего звена, обеспечивающего совпадение ЛЧХ разомкну­тых желаемой и скорректированной САУ. После получения такой передаточной функции могут быть осуществлены ее аппроксима­ция и подбор соответствующего «ближайшего» из существующих корректирующих звеньев. Затем проводится анализ скорректиро­ванной системы и, если она не удовлетворяет требованиям (7.31), делается следующая итерация синтеза.

Корневые методы синтеза применительно к САУ основаны на построении траекторий корней характеристического полинома пе­редаточной функции (7.10) в зависимости от изменений синтези­руемых параметров W_uy (p) в предположении, что структура W_uy (p) — известна. В качестве критерия синтеза используется, в частности, степень устойчивости САУ η.

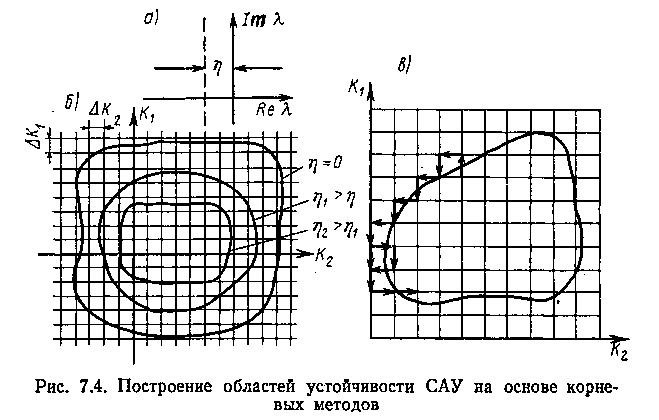
Рассмотрим параметрический синтез по двум параметрам функ­ции W_uy(p), К₁ и K₂, в зависимости от степени устойчивости ri (рис. 7.4, а). В случае двух параметров К₁ , K₂ уравнение (6.1) имеет вид

Построение К₁=F(К₂) осуществляется следующим способом (рис. 7.4,6). Плоскость К₁ , K₂ разбивается сеткой с выбранным шагом на квадраты ΔК₁ x Δ K₂ при замороженных значениях К₂ проходят вое узлы К₁ выводятся на печать те значения K₂, К₁ при которых происходит пересечение границы области устойчиво­сти; уточняют границу путем дробления сетки

Процесс вычислений становится более эффективным, если вос­пользоваться правилом Лоэба (рис. 7.4, в).

Сущность метода для плоскости состоит в следующем: измене­ние параметров может происходить только в четырех возможных направлениях — вправо, влево, вверх, вниз. Перемещения осуще­ствляются только во взаимно перпендикулярных направлениях. Если выполняется условие Re(λ_i)<0, то следующий шаг осущест­вляется с поворотом по часовой стрелке, а если Rе(λ_i))>0, то против часовой стрелки. В случае сложной конфигурации грани­цы возможны различные прямоугольные пути движения, устанав­ливаемые логикой движения в одном направлении (рис. 7.4, в). В том и другом случаях проверка на устойчивость осуществляется с помощью вычисления корней уравнения (7.34) в соответствую­щих узлах сетки. При этом каждый раз пересчитываются коэф­фициенты характеристического уравнения а_i(К₁ , K₂ ).

Общим недостатком изложенных в этом параграфе методов, помимо трудностей их применения к многомерным САУ, является то обстоятельство, что в результате синтеза мы получаем лишь предварительную структуру и начальные значения параметров ре­гулятора. При этом необходимо продолжение синтеза с учетом дополнительных критериев и ограничений, накладываемых на САУ при полных моделях неизменяемой их части. Такое «продолжение синтеза» можно свести к оптимизации параметров машинно-ана­литическим методом (см. гл. 6) для конкретных САУ и специально машинными методами, которые излагаются в следующем пара­графе.