
- •Часть I р. И. Сольницев
- •Глава 1 Введение в автоматизацию проектирования систем автоматического управления
- •§ 1.1. Системы автоматического управления (сау) как объекты проектирования
- •§ 1.2. Сапр как новые средства проектирования
- •§ 1.3. Этапы истории развития сапр сау.
- •Автоматизация проектирования систем и средств управления
- •Дерево целей проектирования:
- •История развития сапр.
- •Задача векторной оптимизации.
- •Глава 2 процесс проектирования сау и его автоматизация
- •§ 2.1. Цели, критерии и условия ограничений процесса проектирования
- •§ 2.2. Этапы проектирования и проектные процедуры
- •Математическая модель Системы Проектирования (сп) как «спирали проектирования»
- •Глава 3 структура системы автоматизации проектирования сау
- •§ 3.1. Концепция, принципы и их структурная реализация
- •§ 3.2. Техническое обеспечение.
- •§ 3.3. Математическое обеспечение
- •§ 3.4. Лингвистическое обеспечение
- •§ 3.5. Программное обеспечение
- •§ 3.6. Информационное обеспечение
- •§ 3.7. Методическое и организационное обеспечение
- •Глава 4 автоматизация построения математических моделей сау
- •§ 4.1. Методы построения математических моделей и их применение в сапр
- •§ 4.2. Вывод математических моделей в аналитическом виде на эвм
- •§ 4.3. Упрощение и преобразование математических моделей на эвм
- •Математическое обеспечение сапр.
- •Стационарные линейные детерминированные модели систем с сосредоточенными параметрами.
- •Переход от дифференциальных уравнений n – ого порядка к нормальной форме Коши
- •Математические модели элементов сау.
- •Методы линеаризации уравнений
- •Глава 5 моделирование систем автоматического управления
- •§ 5.1. Методы моделирования и их применение в сапр
- •§ 5.2. Приведение математических моделей сау к виду, удобному для моделирования
- •§ 5.3. Численные методы и алгоритмы моделирования
- •§ 5.4. Контроль и оценка точности моделирования
- •Глава 6 автоматизация анализа сау
- •§ 6.1. Методы анализа сау и их применение в сапр
- •6.2§. Машинные методы анализа
- •§ 6.3. Машинно-аналитический метод анализа
- •§ 6.4. Подсистема сапр сау «Анализ»
- •Глава 7 Автоматизация синтеза сау
- •§ 7.2. Машинные методы синтеза
- •§ 7.3. Подсистема сапр сау «Синтез»
- •Методы нлп
- •Задача нлп
- •Градиентный метод оптимизации
- •Метод градиента
- •Метод случайного поиска
- •Метод Даниленко-Каган
- •Метод Трахтенбергп
- •Экстраполяционный случайный поиск с адаптирующимся шагом
- •Алгоритм с перестройкой вероятностных характеристик поиска
- •Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов
- •Локально – глобальный поиск коллективом автоматов имени Буша – Мостселлера.
- •Методика выбора алгоритмов поисковой оптимизации.
- •Метод ситуационного управления:
§ 5.2. Приведение математических моделей сау к виду, удобному для моделирования
Приведение к виду, удобному для моделирования, одинаково необходимо как при моделировании на АВМ, так и при моделировании на ЦВМ, поскольку непосредственная реализация исходных ММ САУ оказывается практически невозможной из-за несоответствия этих ММ средствам их воспроизведения на ЭВМ (существующие численные методы интегрирования, соответствующие лингвистические и программные компоненты, возможности самих ЭВМ). Такое несоответствие устраняется путем понижения порядка исходных уравнений, замены переменных и других эквивалентных преобразований с целью исключения неустойчивых звеньев, операций дифференцирования, «не реализуемых» на ЭВМ нелинейных звеньев.
Средствами подсистемы САПР САУ «Упрощение и преобразование ММ» (см. § 4.3) удается в значительной степени автоматизировать преобразования ММ. В дополнение к этим средствам рассмотрим здесь ряд типичных методов и алгоритмов приведения исходных ММ САУ к. виду, удобному для моделирования.
В том случае, когда исходная ММ соответствует верхнему уровню представления САУ и задана в виде структурной схемы или графа (см. § 4.1, рис. 4.1), ввиду того что численные методы моделирования на ЭВМ разработаны, как правило, для форм ММ (3.10), (3.15), возникает необходимость преобразования структурных и графовых ММ к этим формам. Наиболее удобной формой ММ, широко применяемой при математическом моделировании, является форма Коши (3.10). Последовательность операций соответствующего алгоритма продемонстрируем на примере.
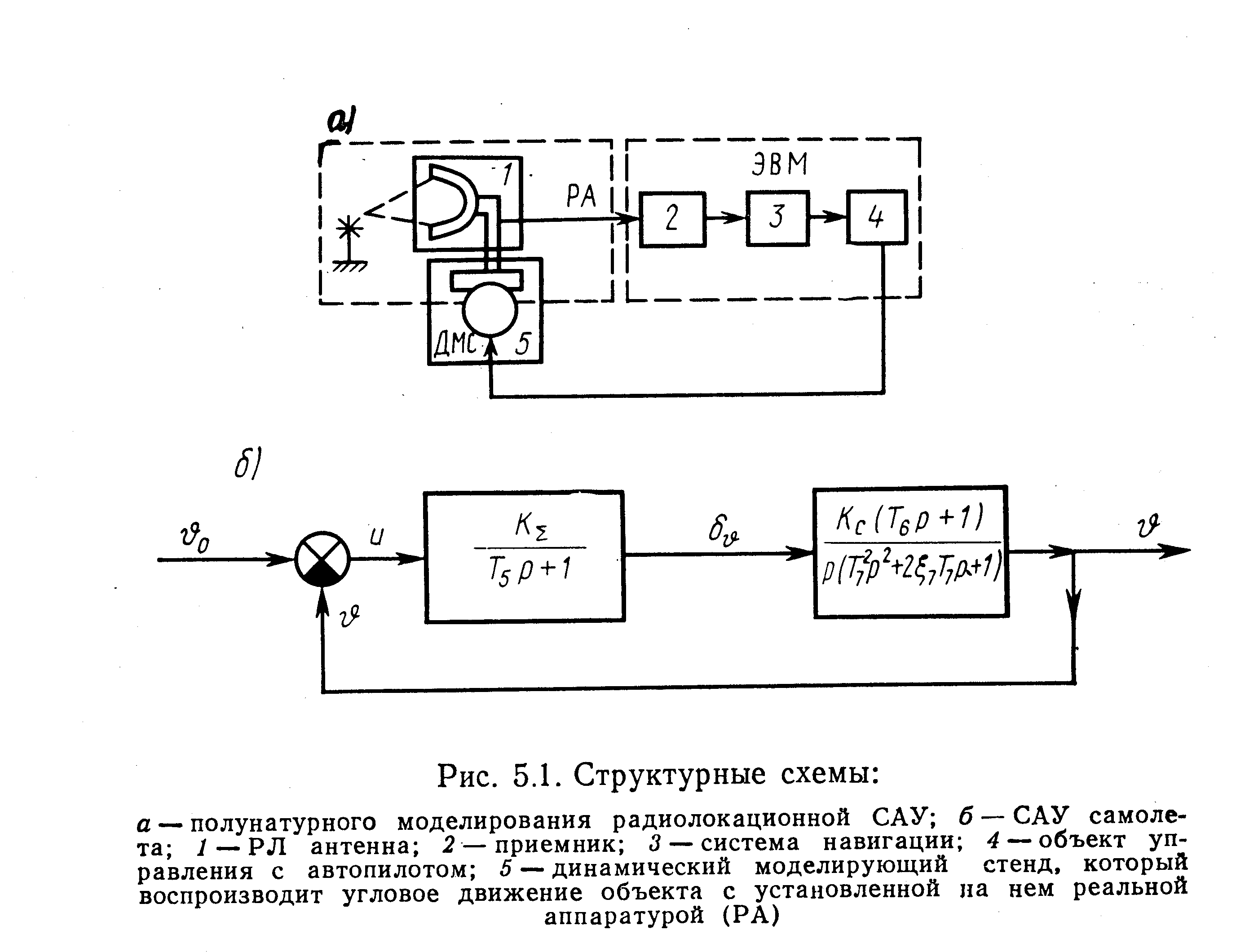

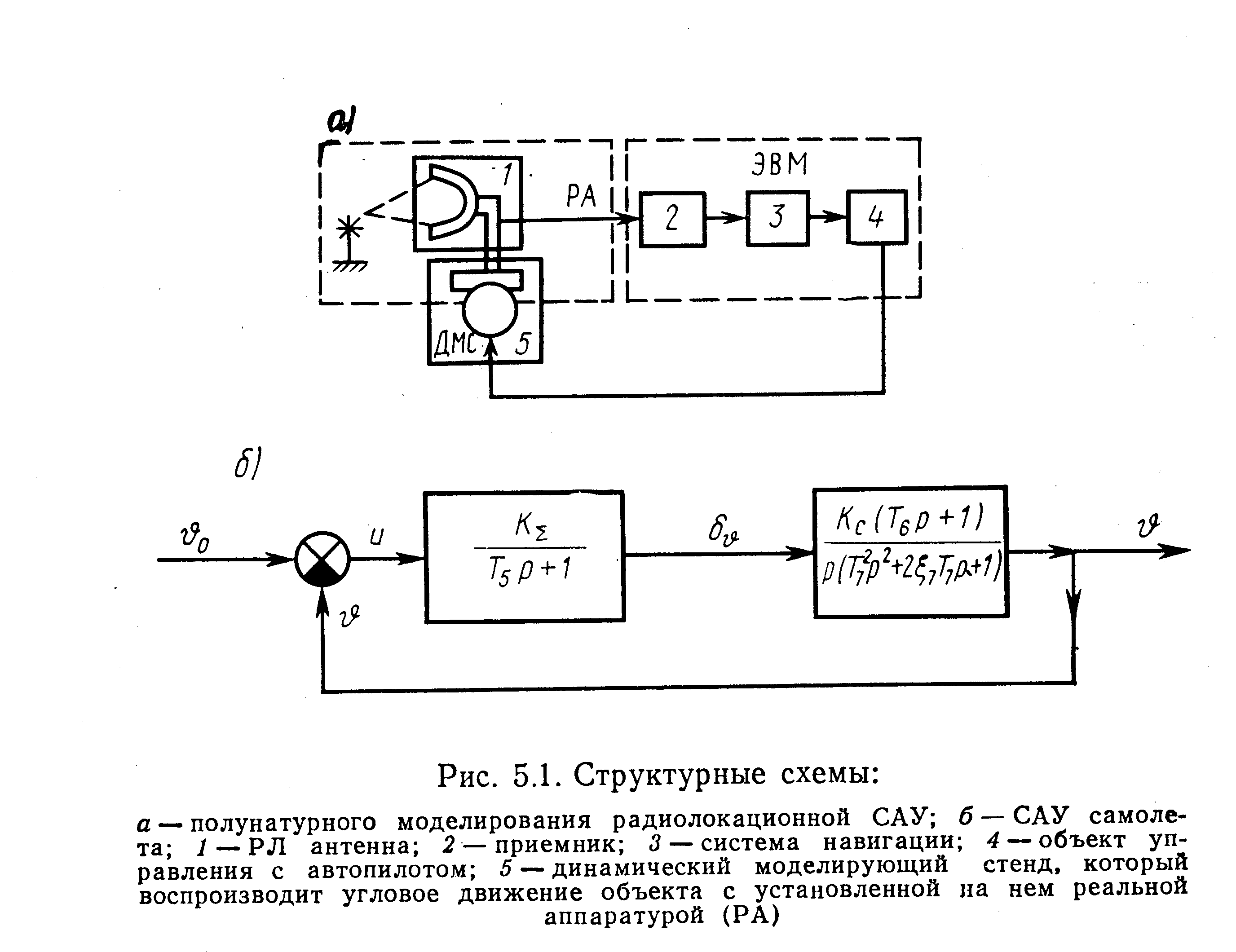
Пример 5.2. Приведение к форме Коши ММ, заданной участком структурной схемы САУ ЛА по тангажу (рис.5.1,б).
Следуя принятой на структурной схеме (рис.5.1,б) последовательности звеньев, запишем уравнения операторов в нормальной форме: для первого звена
![]()
для второго звена

Переписывая эти уравнения в матричной форме (3.15), получим

где
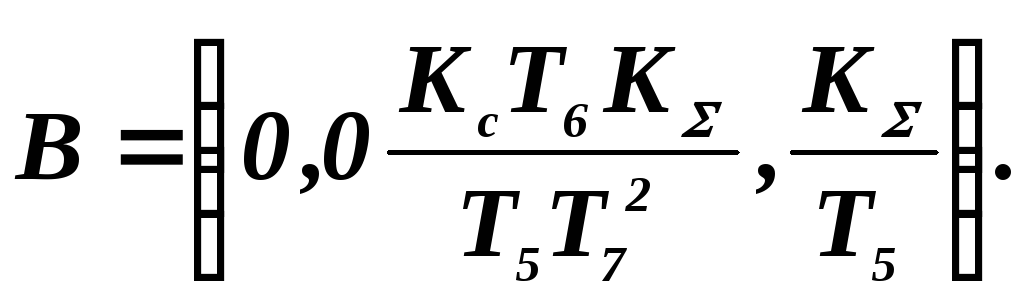
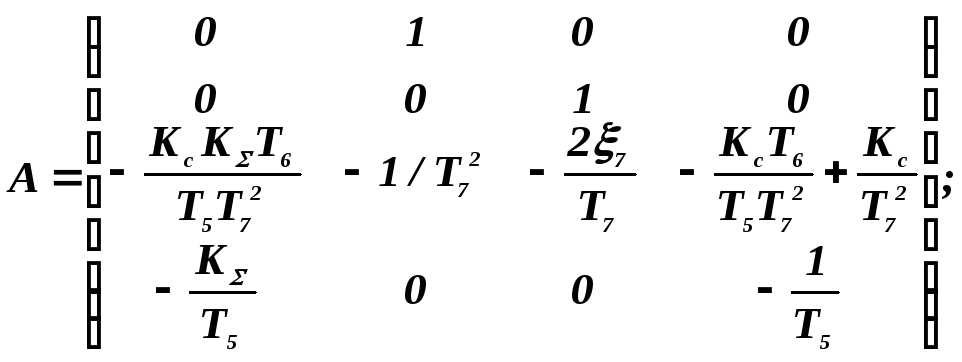
ММ в форме графов приводятся к форме Коши аналогично, только преобразованиям подвергаются операторы дуг графа.
Рассмотрим способы приведения к форме Коши (3.10), (3.11) обобщенных стохастических уравнений (3.7) и форм (3.8), (3.12) — (3.14). Начнем с общей формы (3J7). Прямой ввод в ЦВМ случайных процессов X(t) при большей размерности вектора X приводит к быстрому заполнению памяти ЦВМ и снижению ее быстродействия. Значительные затруднения также вызываются случайным характером вектора начальных условий Y0 и вектора параметров λ, которые приходится задавать раздельно.
В процессе приведения (3.7) к виду, удобному для моделирования, стремятся избавиться от этих недостатков.
Для
придания однородности исходной форме
(3.7) введем начальные условия
![]() в число параметров
с помощью замены
в число параметров
с помощью замены
![]() Тогда
вместо (3.7) получим
Тогда
вместо (3.7) получим
![]() (5.1)
(5.1)
Введем новый вектор параметров большей размерности
![]()
тогда вместо (5.1) можем записать
![]() (5.2)
(5.2)
Учитывая, что каждая составляющая вектора Х(t) задается ансамблем своих реализаций
![]()
![]() где N
– номер эксперимента, случайную функцию
xi(t)
можно рассматривать как функцию двух
переменных xi(t,N).На
ЭВМ функцию xi(t,
N)
воспроизводят с
помощью программ — генераторов случайных
величин — либо с помощью генераторов
реализаций случайных функций.
где N
– номер эксперимента, случайную функцию
xi(t)
можно рассматривать как функцию двух
переменных xi(t,N).На
ЭВМ функцию xi(t,
N)
воспроизводят с
помощью программ — генераторов случайных
величин — либо с помощью генераторов
реализаций случайных функций.
Оба указанных способа применяются при моделировании на АВМ. При моделировании на ЦВМ предпочитают первый способ. Но для реализации этого способа требуется приведение случайных функций к случайным величинам. В настоящее время разработаны способы представления случайных функций как детерминированных зависимостей от случайных величин. При этом следует стремиться к получению возможно меньшего количества случайных величин с целью экономии ресурсов ЦВМ.
Случайный процесс xi(t) представляют в виде
![]() (5.3)
(5.3)
где mi(t) — математическое ожидание; Vk — независимые случайные величины;
φk — детерминированные функции, обычно ортогональные на отрезке 0<t<=T (например, функции в ряде Фурье). Однако представление (5.3) требует весьма большого числа величин Vk и, следовательно, генераторов этих величин. Поэтому вместо линейного разложения (5.3) используется нелинейное
![]() (5.4)
(5.4)
с конкретной реализацией функции в виде
![]() (5.5)
(5.5)
Тогда после известных преобразований
![]() (5.6)
(5.6)
где А, , - случайные величины, а уравнение (5.») перепишем в виде
![]() (5.7)
(5.7)
где
![]() (5.8)
(5.8)
![]()
ММ (5.7) уже достаточно удобна для реализации на ЭВМ с помощью генераторов случайных величин, однако перед последующими этапами ее реализации на ЭВМ необходимо осуществить приведение к форме Коши (3.10). Для упрощения такого приведения будем считать, что (5.7)—детерминированная система дифференциальных уравнений, и поскольку векторы U и μ в дальнейшем не влияют на преобразования, (5.7) перепишем в виде
![]()
Если уравнение (5.9) разрешено относительно Z’’, то приведение в форме Коши выполняется средствами подсистемы «Построение ММ» и сводится к алгоритму

Уравнения в форме (5.10) удобны при математическом моделировании, так как в большинстве случаев именно для этой формы составляются соответствующие стандартные программы численного интегрирования.
В том случае, когда уравнение (5.9) не разрешено относительно старшей производной, вместо (5.10) получим
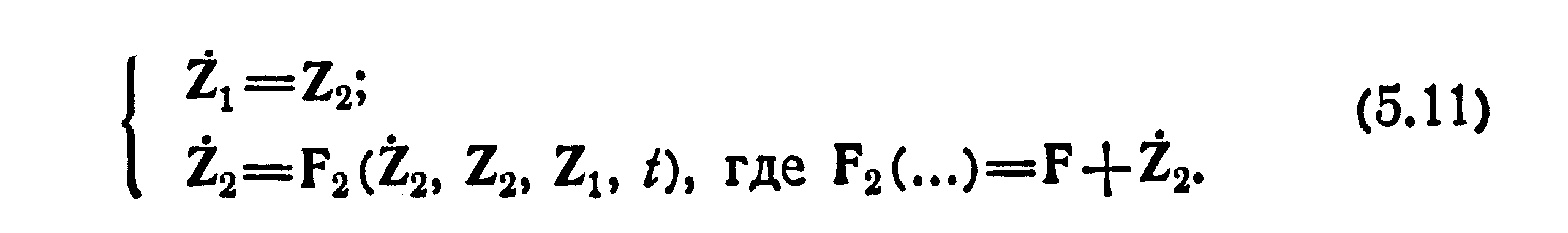
Приведение
этого уравнения к форме Коши в общем
случае — "весьма сложная задача.
Один из подходов в решении этой задачи
состоит в следующем. Для разрешения
последнего уравнения системы (5.11)
относительно Z’2
воспользуемся формулой Ньютона по
отношению к Z’2.
Положим
![]() Тогда
Тогда
![]()
где
![]() (5.12)
(5.12)
Заменяя последнее уравнение системы (5.11) на уравнение (5.12), получим систему в «псевдоформе» Коши:
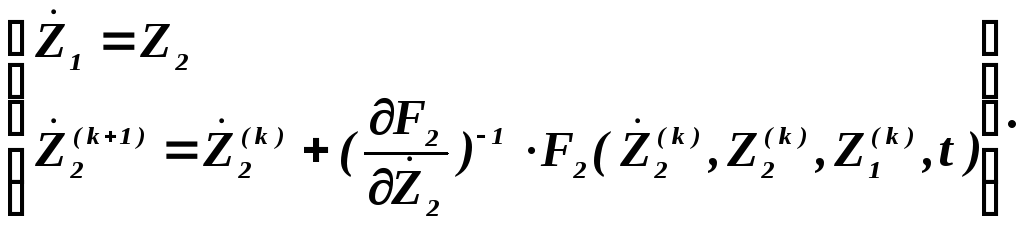 (5.13)
(5.13)
Процесс решения системы (5.13) складывается из численного интегрирования системы (5.13) и итерационной последовательности для последнего алгебраического уравнения на каждом шаге.
Определенные приемы необходимы для приведения уравнений (3.12) — (3.14) к виду, удобному для моделирования на ЦВМ. Приведение к форме Коши уравнений (3.13), (3.14) в том случае, когда правая часть содержит только функцию возмущений X(t), осуществляется просто. Трудности возникают при наличии в правой части (3.13), (3.14) производных от X(t), как, например, для широко распространенного скалярного уравнения вида
![]()
де b0(t), b1(t), ..., bn(t)—коэффициенты, аналогичные a0(t), a1(t), ..., an(t). Рассмотрим приведение к форме Коши такого уравнения, ограничиваясь здесь дифференциальным уравнением с постоянными коэффициентами. Приведение в этом случае осуществляется с помощью последовательной замены переменных. Введем новые переменные и1, u2, ..., ип по формулам
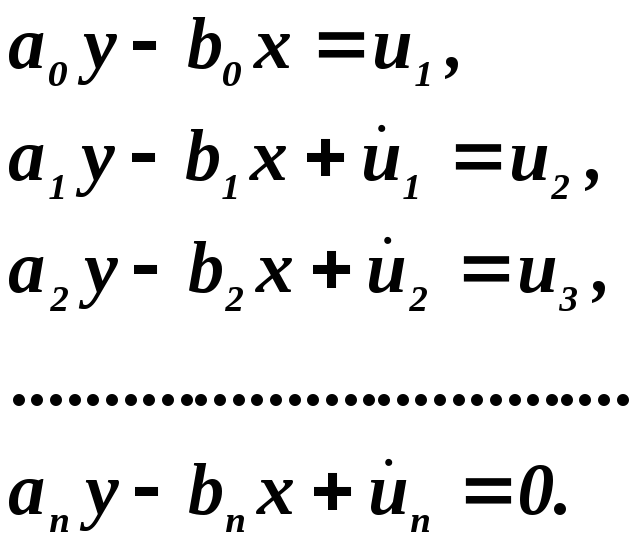 (5.15)
(5.15)
Тогда
 (5.16)
(5.16)
Переписывая
(5.16) в матричной форме
![]() для матриц А и В получим выражения
для матриц А и В получим выражения
 (5.17)
(5.17)
Рассмотрим теперь приведение к форме Коши линейных дифференциальных уравнений в форме (3.16):
![]() (5.18)
(5.18)
В (5.18) матрицы можно представить в виде
![]()
 (5.19)
(5.19)
где
![]() s
– порядки производных. Из (5.19) следует
порядок действий приведения к форме
Коши:
s
– порядки производных. Из (5.19) следует
порядок действий приведения к форме
Коши:
![]() (5.20)
(5.20)
Разрешая это уравнение относительно старшей производной, найдем
![]() (5.21)
(5.21)
Уравнение (5.21) имеет вид одиночного скалярного уравнения, поэтому с ним поступим аналогично скалярному случаю. Введем обозначения:
 (5.22)
(5.22)
где
![]()
Тогда (5.22) в обобщенной форме будет иметь вид
![]()
где
В том случае, когда требуется исключить производные от правых частей в (5.21), строим алгоритм аналогичный (5.16), вводя новые переменные.
