
- •Часть I р. И. Сольницев
- •Глава 1 Введение в автоматизацию проектирования систем автоматического управления
- •§ 1.1. Системы автоматического управления (сау) как объекты проектирования
- •§ 1.2. Сапр как новые средства проектирования
- •§ 1.3. Этапы истории развития сапр сау.
- •Автоматизация проектирования систем и средств управления
- •Дерево целей проектирования:
- •История развития сапр.
- •Задача векторной оптимизации.
- •Глава 2 процесс проектирования сау и его автоматизация
- •§ 2.1. Цели, критерии и условия ограничений процесса проектирования
- •§ 2.2. Этапы проектирования и проектные процедуры
- •Математическая модель Системы Проектирования (сп) как «спирали проектирования»
- •Глава 3 структура системы автоматизации проектирования сау
- •§ 3.1. Концепция, принципы и их структурная реализация
- •§ 3.2. Техническое обеспечение.
- •§ 3.3. Математическое обеспечение
- •§ 3.4. Лингвистическое обеспечение
- •§ 3.5. Программное обеспечение
- •§ 3.6. Информационное обеспечение
- •§ 3.7. Методическое и организационное обеспечение
- •Глава 4 автоматизация построения математических моделей сау
- •§ 4.1. Методы построения математических моделей и их применение в сапр
- •§ 4.2. Вывод математических моделей в аналитическом виде на эвм
- •§ 4.3. Упрощение и преобразование математических моделей на эвм
- •Математическое обеспечение сапр.
- •Стационарные линейные детерминированные модели систем с сосредоточенными параметрами.
- •Переход от дифференциальных уравнений n – ого порядка к нормальной форме Коши
- •Математические модели элементов сау.
- •Методы линеаризации уравнений
- •Глава 5 моделирование систем автоматического управления
- •§ 5.1. Методы моделирования и их применение в сапр
- •§ 5.2. Приведение математических моделей сау к виду, удобному для моделирования
- •§ 5.3. Численные методы и алгоритмы моделирования
- •§ 5.4. Контроль и оценка точности моделирования
- •Глава 6 автоматизация анализа сау
- •§ 6.1. Методы анализа сау и их применение в сапр
- •6.2§. Машинные методы анализа
- •§ 6.3. Машинно-аналитический метод анализа
- •§ 6.4. Подсистема сапр сау «Анализ»
- •Глава 7 Автоматизация синтеза сау
- •§ 7.2. Машинные методы синтеза
- •§ 7.3. Подсистема сапр сау «Синтез»
- •Методы нлп
- •Задача нлп
- •Градиентный метод оптимизации
- •Метод градиента
- •Метод случайного поиска
- •Метод Даниленко-Каган
- •Метод Трахтенбергп
- •Экстраполяционный случайный поиск с адаптирующимся шагом
- •Алгоритм с перестройкой вероятностных характеристик поиска
- •Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов
- •Локально – глобальный поиск коллективом автоматов имени Буша – Мостселлера.
- •Методика выбора алгоритмов поисковой оптимизации.
- •Метод ситуационного управления:
§ 5.3. Численные методы и алгоритмы моделирования
Поскольку мы строим процессы моделирования на основе решения задачи Коши, будем исходить из уравнения (3.10), переписав его здесь для простоты в виде
![]() (5.24)
(5.24)
Далее достаточно будет рассмотреть скалярное уравнение
![]() (5.25)
(5.25)
Численным решением уравнения (5.25) является таблица, которая на каждом шаге h дает числовые значения переменной у’ (k, h) достаточно близкие к истинным значениям y(k, h).
Классические методы численного интегрирования обыкновенных дифференциальных уравнений восходят к Л. Эйлеру (российский математик и механик, 1707—1783), Д. Адамсу (английский математик, 1812—1892), К. Рунге (немецкий математик, 1856—1927), А. Н. Крылову (математик и инженер, член АН СССР, 1863—1945). Появление ЦВМ и бурное их развитие для решения широкого круга задач науки и техники потребовало переоценки классических методов численного интегрирования, их машинной ориентации и разработки новых, собственно машинных методов, учитывающих специфику ЦВМ. Машинная ориентация классических численных методов состоит в распространении этих методов на системы уравнений большой размерности, автоматизации операций реализации методов на ЭВМ, выбору наиболее подходящих методов и алгоритмов для решения конкретной задачи и величины шага h в этих алгоритмах.
Численные методы, основанные на классическом разложении правых частей (5.25) в степенные ряды Тейлора в аналитической форме, обычно исключаются из практического применения ввиду необходимости вычислений производных функций f(y,-t) порядка л>1. Однако применение ППП «Аналитические преобразования» (см. § 4.2) позволяет для ряда ММ САУ «заготавливать» эти производные в аналитическом виде, что принципиально меняет возможности применения численных методов на степенных разложениях, делает их эффективными. В соответствии с отмеченными обстоятельствами рассмотрим построение таких методов. Будем искать решения (5.25) в форме ряда

сходящегося на промежутке 0<=t<=R. Тогда все дело сводится к нахождению неопределенных коэффициентов ak, k принадлежит множеству от 0, до бесконечности, в (5.26). Для этого подставим (5.26) в (5.25), предварительно разложив f(y, t) в ряд Тейлора относительно точки t=0, у = уо:
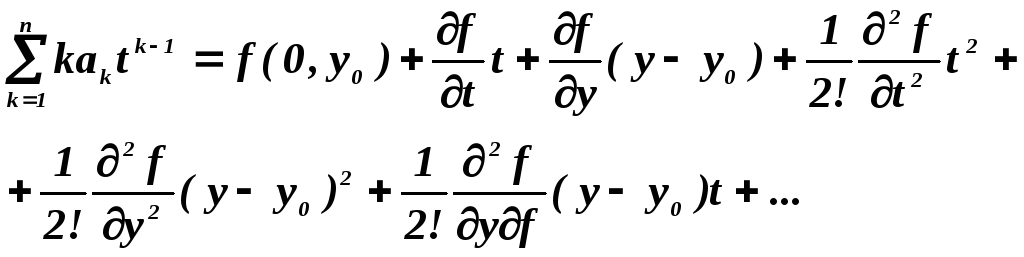
Приравнивая в этом разложении коэффициенты при одинаковых степенях t, найдем
 (5.27)
(5.27)
Таким образом, можно последовательно найти аk и тем самым построить решение (5.26).
Однако этот алгоритм обладает существенными недостатками— необходимостью ограничиваться только промежутком сходимости ряда (5.26), оперировать с большим числом членов этого ряда и брать производные высокого порядка от правой части в (5.25). От первого недостатка мало избавиться воспользовавшись аналитическим продолжением решения y(t)
![]()
где tj— переменный центр разложения, a (t—tj)<R, j=0, 1, 2, ..., t0 = 0 (рис. 5.2, а).
В этом случае коэффициенты разложения ak каждый раз пересчитываются для нового центра разложения //, у$.
От второго недостатка избавляются применением асимптотического представления у (t):
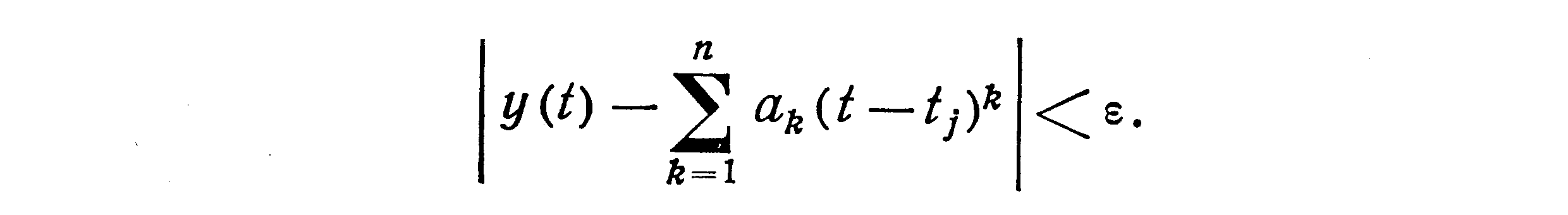
Для асимптотического представления y(t) удобно воспользоваться формулой Тейлора в точке t = tj:
![]() (5.28)
(5.28)
где
![]() -
остаточный член, представляющий малую
величину вышеn-ого
порядка; y(t)(tj)
– i-ая
производная от
-
остаточный член, представляющий малую
величину вышеn-ого
порядка; y(t)(tj)
– i-ая
производная от
![]()
В теории рядов Тейлора доказано, что если для какой-либо функции (t), имеющей производные n-ого порядка включительно, в точке t=h выполняется условие
![]() (5.29)
(5.29)
то
![]() и
и![]() и представляет собой бесконечную малую
порядка малости вышеn.
Тогда, обозначив в (5.28)
и представляет собой бесконечную малую
порядка малости вышеn.
Тогда, обозначив в (5.28)
![]()
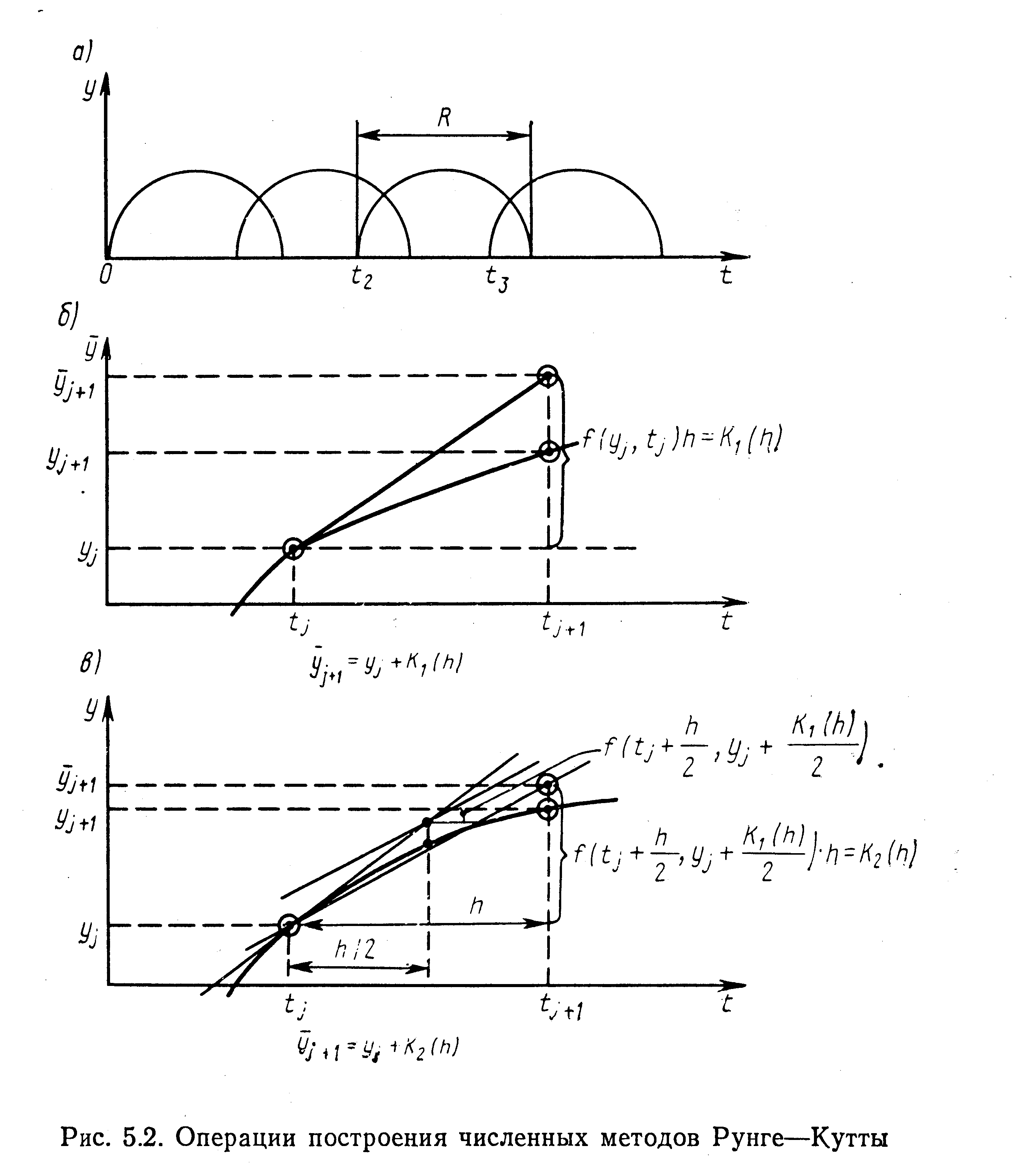
и обеспечив выполнение условия (5.29) выбором п и h, получим

На
промежутке
![]() асимптотическое разложениеy(t)
примет вид
асимптотическое разложениеy(t)
примет вид
![]() (5.30)
(5.30)
В этом выражении есть два регулируемых параметра: п и h . Выбором этих параметров можно добиваться точности порядка hn+l при числе членов разложения п. Имеющиеся в составе САПР
САУ средства программирования позволяют автоматически получать аналитические выражения для y(i)(t) в (5.30). Поэтому процедуру численного интегрирования уравнения (5.25) можно построить в соответствии с алгоритмом (5.27), возложив на ЭВМ определение производных, расчет коэффициентов аi выбор шага h<=R. Распространение алгоритма (5.27), составленного для скалярного уравнения на систему уравнений (3.10), состоит в вычислении производных и в составлении в аналитическом виде коэффициентов для векторного уравнения
![]() (5.31)
(5.31)
где dF/dt — вектор, полученный покомпонентным частным дифференцированием, a dF/dY есть (n1xn1) матрица Якоби функции F(Y, t) системы (3.10), в которой для простоты положено X=λ=U=0.
Построение численных методов, в которых переход от y’(tj) к y’(tj+1) не требовал бы вычисления производных от правых частей в (5.25), основано на идее Рунге. Принцип построения таких формул численного интегрирования можно усмотреть из геометрических построений (рис. 5.2, б, в). Продолжая этот процесс и организуя комбинации ki(h) для нескольких точек внутри промежутка tj+1—tj, запишем общую формулу этой группы численных методов:
![]() (5.32)
(5.32)
где
![]()
Из (5.32) при различных значениях i, i получим как частные случаи известные формулы численного интегрирования Рунге и Кутта (венгерский математик, 1867-1944) разного порядка точности:
первого порядка
![]() (5.33)
(5.33)
- метод Эйлера;
второго порядка
 (5.34)
(5.34)
- метод Эйлера – Коши;
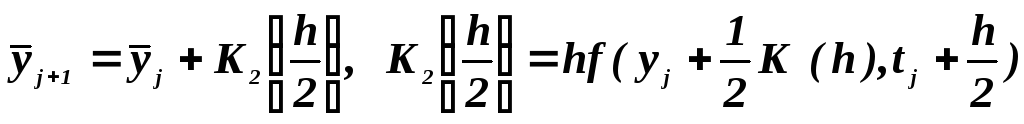 (5.35)
(5.35)
- усовершенствованный метод Эйлера;
четвертого порядка
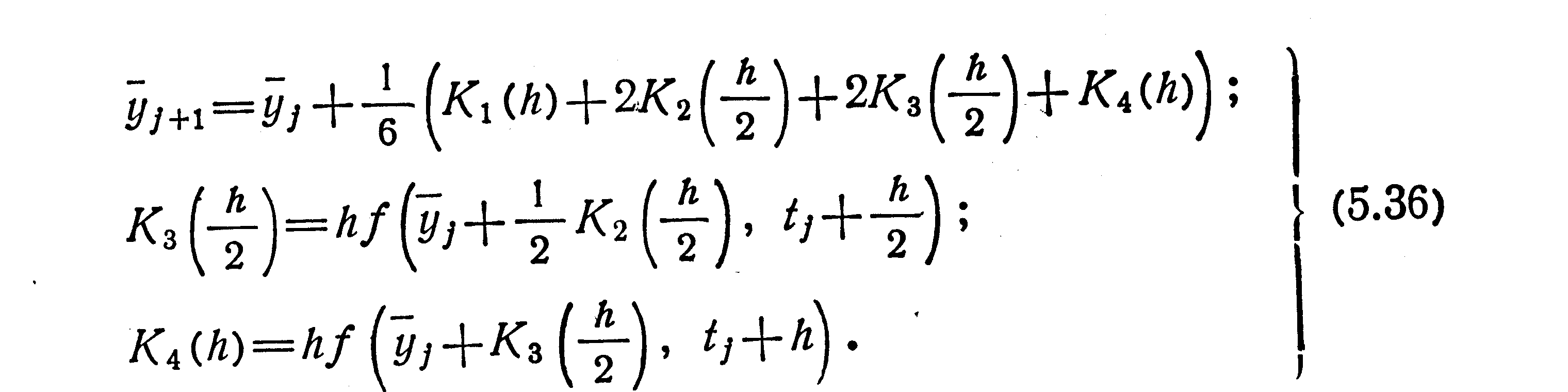
Точность представления у на одном шаге в каждой формуле оценивается остаточным членом разложения функции φ(h) в ряд Тейлора:

Величина r в (5.37) называется порядком точности метода или степенью метода. Важно сразу же отметить, что выбор шага h исходя из заданой точности на одном шаге в принципе не гарантирует требуемой точности конечного результата.
Следующая группа методов численного интегрирования, основанная на идеях Адамса, строится на основе аппроксимации подынтегральной функции в формуле Ньютона—Лейбница
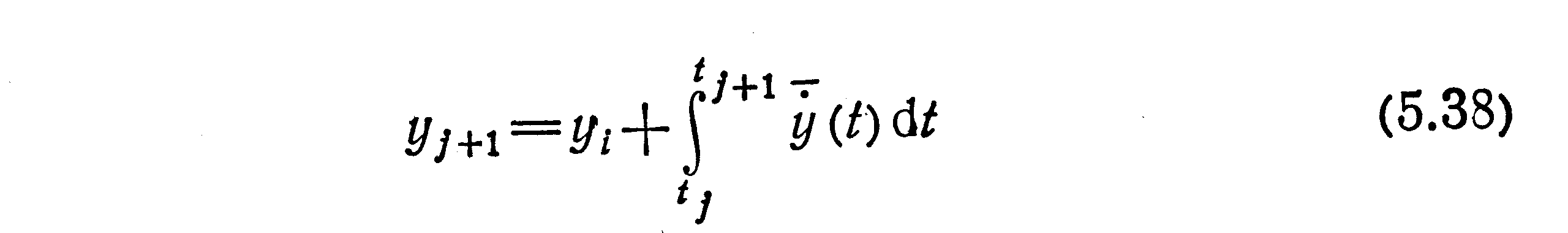
известным полиномом. Эта формула получена после интегрирования уравнения (5.25) на промежутке tj, tj+1. Если в качестве такого полинома выбирать полином Ньютона, то у’ (t) можно представить в виде
![]()
Задавая предыдущие значения y’(tj), y’(tj-1), y’(tj-2)...в предположении, что они вычислены заранее, вычисляем неизвестные коэффициенты:
 (5.40)
(5.40)
где
![]() .
Подставляя (5.40) в (5.38), после интегрирования
получим
.
Подставляя (5.40) в (5.38), после интегрирования
получим

или в общем виде

Методы типа (5.41) называют также многошаговыми в отличие от одношаговых (5.32), так как для получения yj+1 необходимо предварительно вычислить п предыдущих значений yj-k ,k = 0, ..n. Очевидно, недостатком методов этого типа является необходимость предварительного вычисления «разгонных» значений y’(tj-1). Методы (5.32), (5.41) реализованы в виде стандартного программного обеспечения современных ЭВМ.
Применимость методов (5.32), (5.41) к моделированию САУ тесно связана с выбором шага h в формулах численного интегрирования. В случае одного уравнения (5.25) значение h выбирается из соображений точности на одном шаге и оно же обеспечивает устойчивость вычислительного процесса. Когда же рассматривается система уравнений (3.10), то именно устойчивость разностных уравнений (5.32), (5.41) ограничивает шаг. Наибольшие шаги, обеспечивающие устойчивость разностной схемы, или, как их обычно называют, критические шаги, различаются по величине для разных методов. Так, например, если собственные значения вычисленной в данной точке t=t* матрицы Якоби системы (3.10) вещественны, то критический шаг выбирается из соотношения
![]() (5.42)
(5.42)
где λmах — максимальное собственное значение; r — число, зависящее от метода.
Для метода Рунге — Кутты четвертой степени оно равно 2.78, для методов Эйлера и Эйлера — Коши — 2, для метода Адамса четвертой степени — 0,3. Причем даже незначительное увеличение значения h против допустимого приводит к потере вычислительной устойчивости — «взрыву погрешности».


Подобные явления возникают при численном решении задачи Коши не только для САУ, но и для других объектов. Это обстоятельство повлияло на усиленное внимание к разработке специально машинных методов численного интегрирования, учитывающих особенности ЭВМ.
Одна из основных идей таких методов заключается в построении формул численного интегрирования с «обратной связью» — так называемых неявных методов. В неявных методах можно достичь увеличения шага h по сравнению с явными без потери устойчивости вычислительного процесса. В простейшем случае неявный метод получается из формулы (5.38), если воспользоваться формулой правых прямоугольников при взятии интегралов в (5.25):

Аналогично строятся неявные формулы для методов (5.32), (5.41). Например, неявная формула второго порядка будет иметь вид

Методы этого класса являются устойчивыми и не имеют ограничености может выбираться сообразно с требуемой длительностью рений вида (5.42) на величину шага дискретности. Шаг дискретно шения.
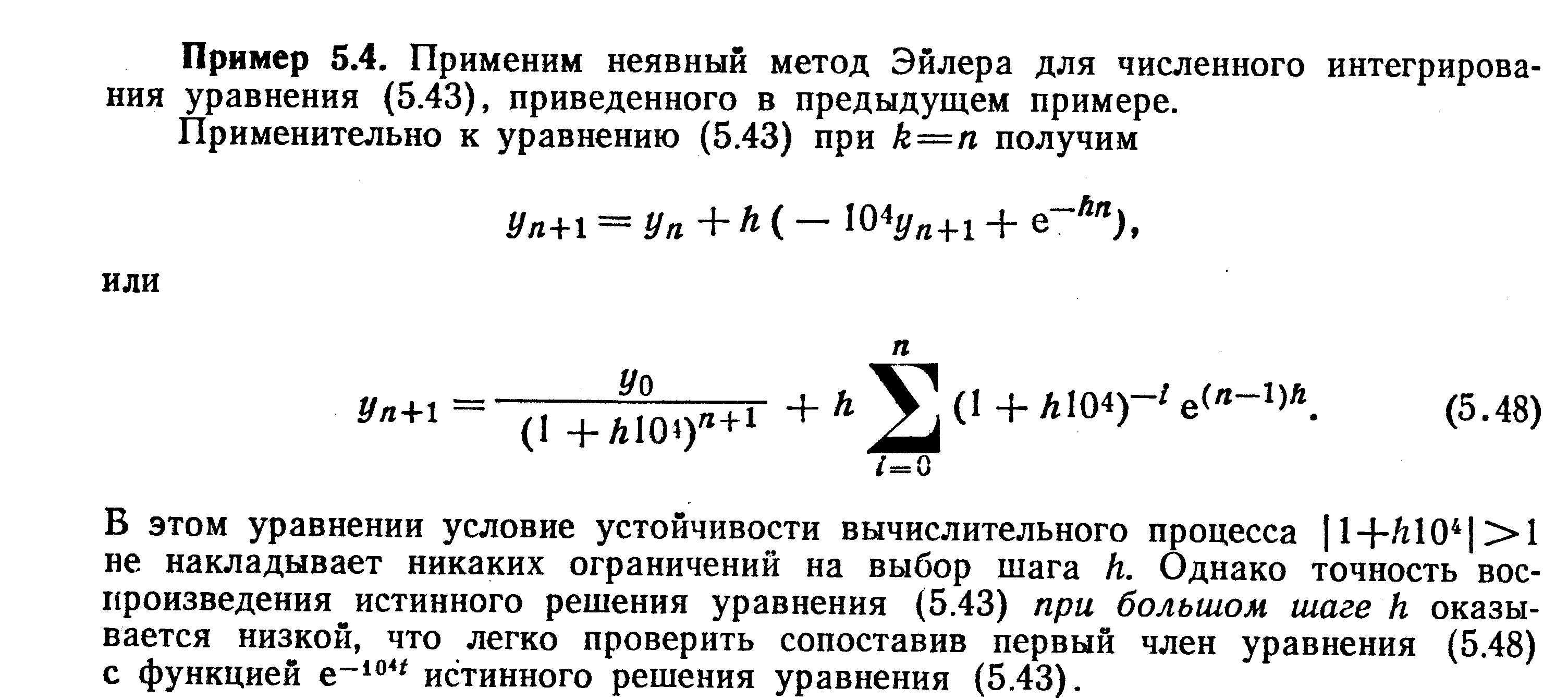
При реализации неявных методов необходимо на каждом шаге решать нелинейные уравнения типа (5.45), что вызывает значительные осложнения и является недостатком этих методов. Поэтому применение неявных методов сочетают со специальными методами решения нелинейных уравнений на каждом шаге.
Так, метод Эйлера (5.45) с модификацией его по формуле Ньютона примет вид

Из других неявных методов приведем методы, предложенные в 1952 г. американскими математиками С. Ф. Куртисом и Н. О. Хиршфельдером, так как их применение оказалось эффективным при моделировании САУ. Неявные алгоритмы Куртиса — Хиршфельдера строятся на принципе «дифференцирования назад» и имеют вид

т. е. в выполнении своеобразного «дифференцирования назад».
Применение неявных методов при моделировании CAY показывает их преимущества над явными в смысле устойчивости вычислительного процесса при увеличении шага, однако точность получения решений существенно зависит от точности решения нелинейных алгебраических уравнений (5.45), (5.49). Причем если в явных методах выбором шага по (5.44) удается получить, хотя и с погрешностью, решение (5.25) качественно верное, то в неявных при неправильном выборе шага можно получить устойчивые решения, но качественно отличные от искомого. Значительные увеличения шага при моделировании САУ неявными методами оказываются ограниченными из-за резкого снижения точности. Практически по сравнению с явными методами удается увеличить шаг не более чем в 5—10 раз.
Эффективное применение неявные методы и алгоритмы нашли в процедуре, предложенной Гиром, с изменениями и дополнениями, внесенными Хиндмаршем (С. В. Гир и А. С. Хиндмарш — американские математики). В процедуре Гира применяются методы (5.49). Однако это не исключает возможности применения и других численных методов. Неявный характер употребляемых в процедуре Гира методов предполагает решение на каждом шаге системы алгебраических уравнений, для чего предусматривается использование трех модификаций итерационного метода Ньютона.
Для этого каждое из уравнений (5.49) представляется в виде
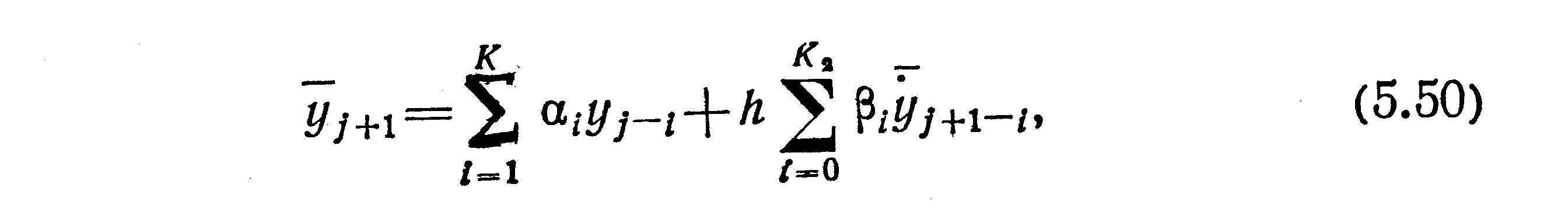
где αi, βi— числовые коэффициенты; К1, K2 — количество соответствующих слагаемых в (5.49).
Pешение нелинейных алгебраических уравнений (5.50) относительно yj+1 строится как следующий процесс:
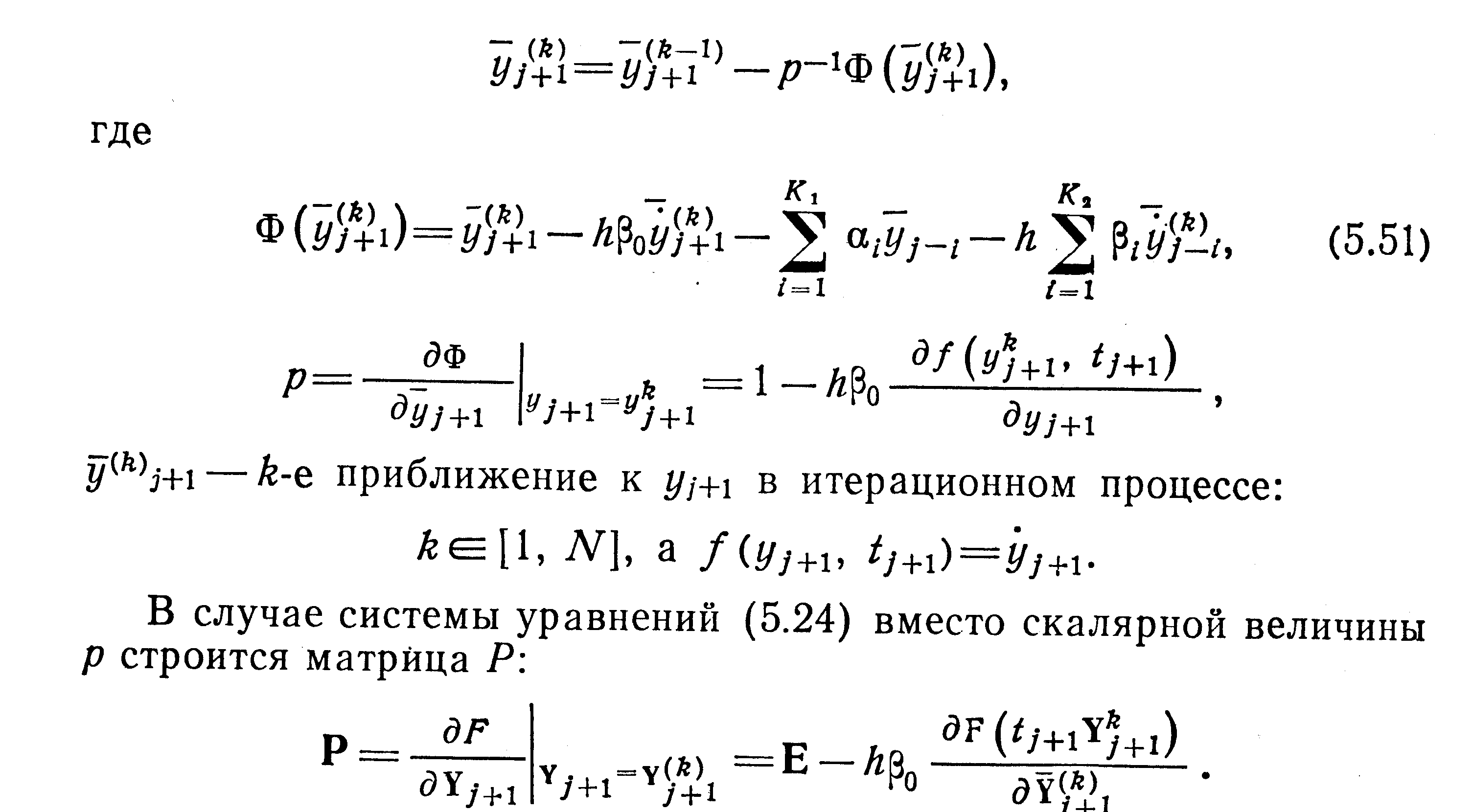
В процедуре Гира автоматически выбираются численный метод и шаг по заданной точности вычислений.
Если в некоторый момент времени используется метод степени l (например, в (5.51) К1 = l, К2=l—1), то одновременно оценивается локальная погрешность методов степени l—1, l+1. В дальнейшем применяется тот метод, который при заданной точности позволяет интегрировать с большим значением шага h.
Еще одно преимущество процедуры Гира в том, что она не требует стартового алгоритма. Интегрирование начинается с методов первой степени, а затем степень метода при необходимости изменяется в соответствии с задаваемой пользователем точностью. Следует отметить, что алгоритмы процедуры подвержены неустойчивости, которая проявляется в колебательном характере шага, принимающем то разумные значения, то неприемлемо малые. Возникающие трудности можно исключить уточняя соответствующие константы αj, βj эмпирическим путем.
Все рассмотренные методы являются скалярными, т. е. для каждого уравнения системы (3.10) составляется соответствующее разностное уравнение, поэтому они обладают присущими скалярным методам недостатками при применении их к системам большой размерности. Качественно новым является создание системных (матричных) методов, которые позволяют учитывать свойства правой части системы (3.10) и обеспечивают независимость выбора шага от устойчивости вычислительного процесса.
Системные методы были предложены Ю. В. Ракитским (советский инженер и математик, 1932—1986). Эти методы построены на введении в разностное уравнение, эквивалентное исходному (3.10), матричного множителя Ф(А, H) который «подобен» шагу интегрирования h в методе Эйлера (5.33):

при этом Hи h связаны соотношением H=h*2N, где h — начальный шаг интегрирования, а точность вычислений Ф0 соответствует точности метода (5.34) при интегрировании системы Y=AY. На рис. 5.4, а приведена последовательность операций по реализации метода (5.52).
Верхняя граница для h удовлетворяет соотношению h <=1/[[A]] а достаточное порочности нижнее значение h определяется сравнением Y(k, h), Y(kh/r), вычисленных при h и h/r.
Рассмотрим теперь системные методы для решения систем линейных уравнений, получаемых из общего уравнения (3.10) после
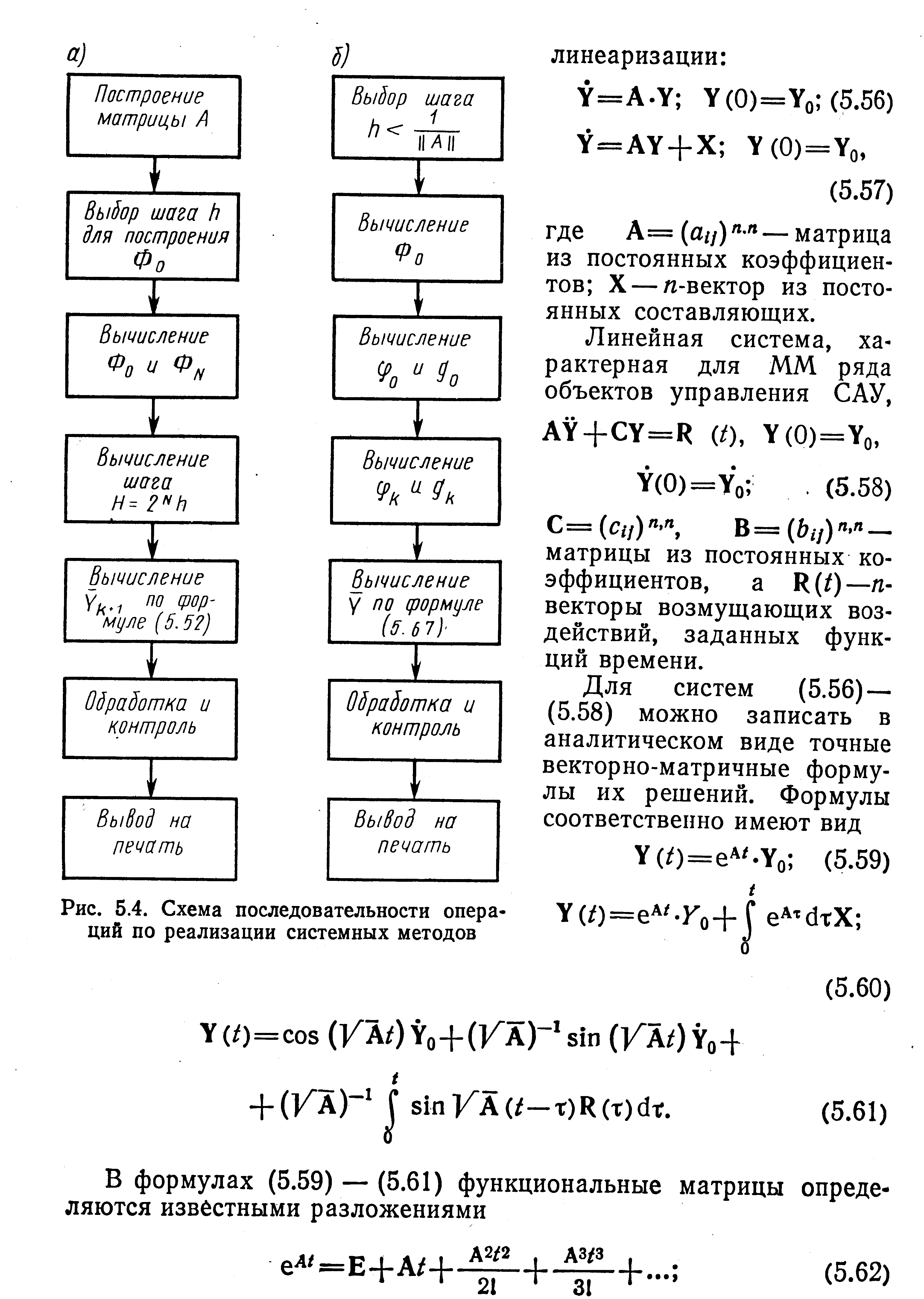

где под √А понимается матрица, для которой (√A)2=A.
Формулы (5.59) — (5.65) определяют Y(t) для любого момента времени. Казалось бы, задача решена и с точки зрения машинной реализации сведена к наиболее простой операции — «счету по формулам». Однако численная реализация этих формул упирается в серьезную проблему вычисления функциональных рядов (5.62) — (5.65). Непосредственное применение формул (5.62) — (5.65) для этой цели при достаточно больших t и плохой обусловленности матрицы А приводит к необходимости учета большого числа членов, увеличивающихся с ростом t, поэтому для организации вычислений от (5.56), (5.57) осуществляется переход к эквивалентным разностным уравнениям, по которым и осуществляется вычисление решения шаг за шагом. Такой переход уже был сделан для системы (3.15) (см. § 3.3, формула (3.26)).
Для систем (5.56), (5.57) эквивалентные разностные уравнения имеют вид
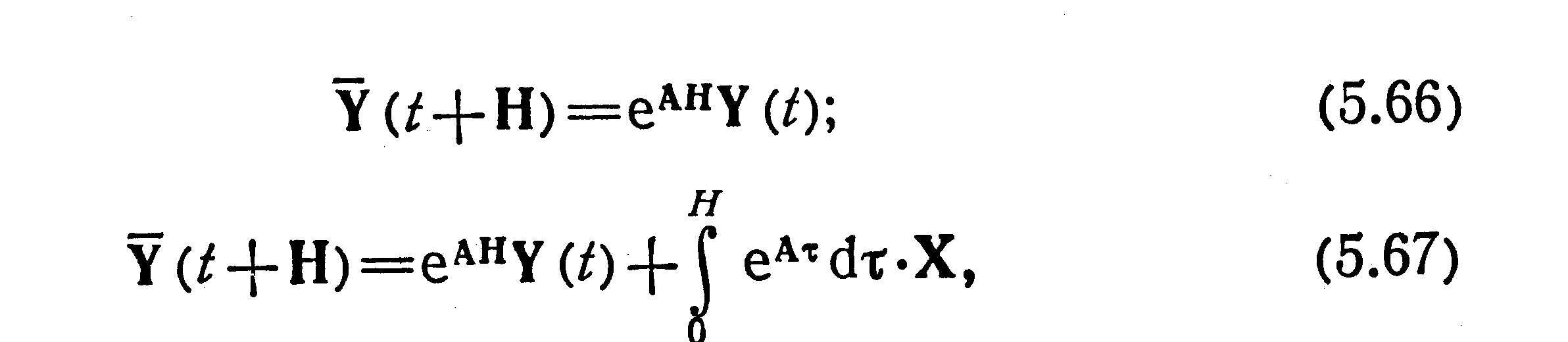
где Н — шаг дискретности, выбираемый из удобства наблюдения процесса Y(t) и не зависящий от свойств этого процесса.
По существу, в (5.66), (5.67) все дело сводится к вычислению матриц еАН и вектора
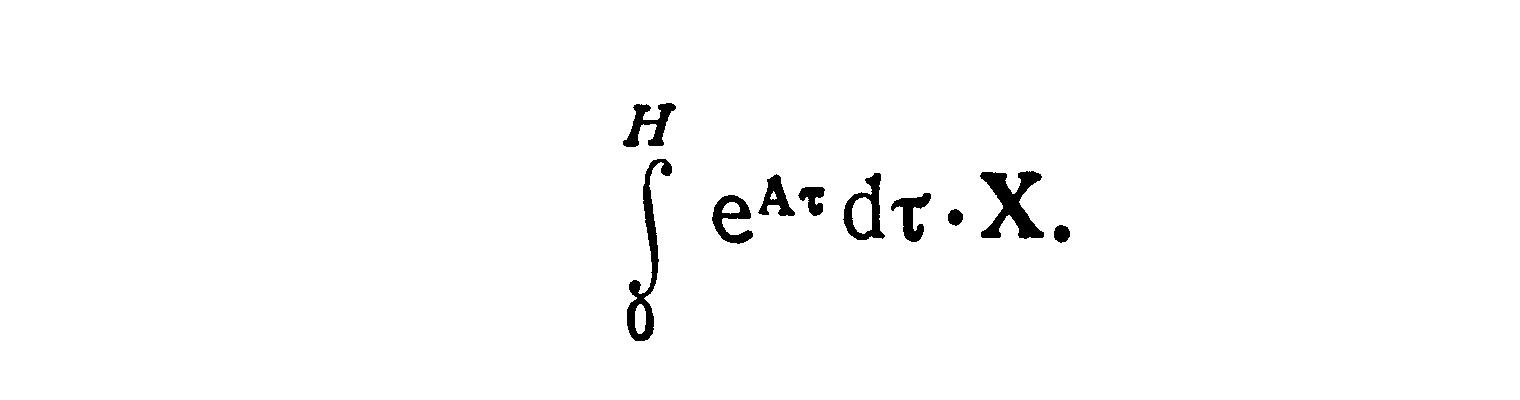
Существует много способов вычисления матрицы еАH , что указывает на сложность этой процедуры и зависимость ее от свойств матрицы А и величины Н. При малых шагах h матрица еАН вычисляется значительно проще. В практике численного интегрирования линейных уравнений, описывающих движение САУ, матрица еАh вычислялась двумя способами: по формуле (5.62) при t=h; путем решения вспомогательного матричного уравнения U = AU, U(0)=E с последовательным формированием еAh по столбцам

Матрица Ф0 вычисляется по формуле (5.55). На рис. 5.4, б приведена последовательность операций по реализации алгоритма (5.69).
Выбор методов и алгоритмов численного интегрирования, подходящих для решения конкретной задачи (3.10) или (5.24), можно проверить исходя из свойств правых частей уравнений (5.24). Для моделирования САУ с числом обусловленности ρ(Я)<103 и временем решения tН<<1 мин вполне приемлемым оказываются скалярные методы (5.32), (5.49).
В случае моделирования САУ с числом обусловленности их ММ ρ(Я)<106 tн<5 мин вполне приемлемыми оказываются неявные методы (5.47), (5.41) с их реализацией в виде процедуры, аналогичной процедуре Гира (см. § 5.3).
Моделирование САУ с числом обусловленности р(Я)>Юб и временем наблюдения /н>5 мин скалярными методами становится малоэффективным, и необходимо применять системные методы (5.52), (5.60) — (5.69).
Практика моделирования САУ с помощью системных методов показывает, что эти методы позволяют существенно — в 20— 30 раз — уменьшить время получения решения по сравнению со скалярными. Это дает возможность эффективно решать задачи моделирования САУ на ЭВМ по полным их моделям. Недостатком системных методов (5.52) является необходимость вычисления матрицы Ф(А, Н) в каждом частном случае и составления специальной программы пересчета шагов.
