§ 4.2. Вывод математических моделей в аналитическом виде на эвм

Расчет и исследование САУ на всех уровнях базируется на ММ двух видов: уравнения динамики и уравнения статики. Пос­ледние получаются из уравнений динамики как частный случай после установления переходных процессов. Так, система уравне­ний в форме (3.7)

(4.21)

является уравнением динамики. Если в этой системе положить 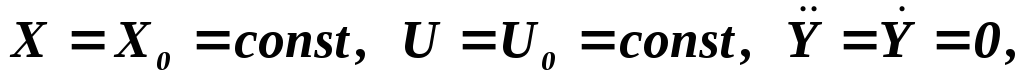что соответствует установившемуся режиму приt=T, то получим уравнение статики

(4.22)

Уравнение (4.22) получается в результате простейшей опера­ции упрощения ММ. В более сложных случаях упрощение полных ММ требует специальных методов и алгоритмов и оказывается обязательной процедурой в общей подсистеме САПР «Построе­ние ММ».

Все выкладки, необходимые для вывода уравнений САУ, обыч­но сводятся с математической точки зрения к последовательному выполнению таких операций, как умножение матрицы на вектор, перемножение матриц, сложение, вычитание, перемножение алге­браических полиномов, дифференцирование сложных функций и приведение подобных членов.

Для автоматизации перечисленных операций с позиции поль­зователя необходимы три условия: язык, допускающий проведе­ние аналитических преобразований данного типа на ЭВМ; соот­ветствующая ЭВМ; устройство диалога человека с ЭВМ в про­цессе составления уравнений.

Если технические средства САПР САУ (см. § 3.3) содержат ЭВМ и ТП, необходимые для выполнения второго и третьего усло­вий, то разработка ПОЯ и ряда программных средств, преду­смотренных в прикладном программном обеспечении САПР САУ (см. § 3.4), становится обязательной для выполнения первого условия успешного построения ММ на ЦВМ.

Если при выводе дифференциальных уравнений «вручную» вы­бор того или иного метода зависит скорее от вкусов исследова­теля, чем от каких-либо вычислительных преимуществ, то при машинном выводе уравнений выбор метода имеет определяющее значение. Дело в том, что количество и вид операций, приемле­мость существующих языков и программ, длительность вычисли­тельного процесса, загрузка оборудования и расход средств на решение во многом определяются принятым методом составления уравнений. В общем случае выбор метода и системы програм­мных средств аналитических преобразований должен подчи­няться зависимости

определяющей разность двух множеств: G — операций исходного алгоритма, представленных на выбранном языке аналитических преобразований, Я — операторов аналитических преобразований, допускаемых выбранной системой программирования.

Анализ алгоритмов вывода по критерию (4.23), а также с точ­ки зрения наименьших затрат машинного времени и подготови­тельных операций оказывается достаточно сложным. Проведениетакого анализа применительно к тестовым задачам вывода урав­нений ЛА, ГСП и других САУ показали, что по соображениям простоты подготовки исходных данных, длины программы, вре­мени счета, объема работы оператора преимущества имеет фор­мализм Лагранжа (4.3).

В соответствии с рассматриваемым классом объектов алго­ритм формирования их ММ должен обеспечивать построение мо­делей как механической, так и электрической, гидравлической и других частей САУ. Формализм Лагранжа представляет единый алгоритм машинного вывода уравнений, одинаково пригодный для всех частей. Действительно, число этих уравнений соответст­вует числу обобщенных координат независимо от того, являются эти координаты механическими, электрическими или какими-либо другими.

Перечисленные обстоятельства являются основанием для вы­бора формализма Лагранжа за основу при разработке алгорит­мов вывода уравнений САУ. В дальнейшем будем рассматривать только механические и электрические устройства САУ. В качестве обобщенных координат будем принимать угловые и линейные пе­ремещения механических элементов и количества электричества, протекающего через сечения проводников электрических элемен­тов. Обозначим через

(4.24)

вектор обобщенных координат механической части и через

(4.25)

вектор обобщенных координат электрической части системы. Тогда кинетическая энергия всей системы может быть представлена выражением

(4.26)

а потенциальная энергия всей системы – выражением

(4.27)

Введем также обобщенные силы демпфирования

(4.28)

где

.

и обобщенные силы внешних воздействий

В выражениях (4.26) — (4.28) обозначено: т_il d_il— механические массы (моменты инерции), статические коэффициенты упругих сил; L_kj, C_kj — электромагнитные и электростатические коэффи­циенты индукции; h_si, r_sj —механические и электрические сопро­тивления; Q_m, Q_e — механические внешние моменты и электриче­ские напряжения от внешних источников — известные функции времени.

Составляя теперь уравнения Лагранжа с учетом (4.27), (4.28), найдем

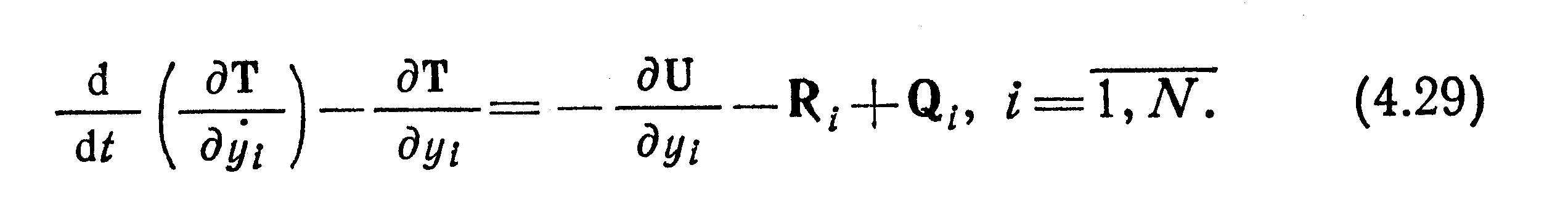
Уравнения (4.29) можно преобразовать исходя из экономичности вычислительного процесса на ЭВМ (уменьшение числа опе­раций, затрат машинного времени и т. д.).

Так, если в дальнейших исследованиях потребуется численное интегрирование полученной ММ, то ее обычно приводят к кано­нической форме. Получение уравнений в канонической форме можно осуществить сразу, если воспользоваться обозначением p_i=dT/dy’_i i=(1, N). Тогда уравнения (4.29) преобразуются к виду

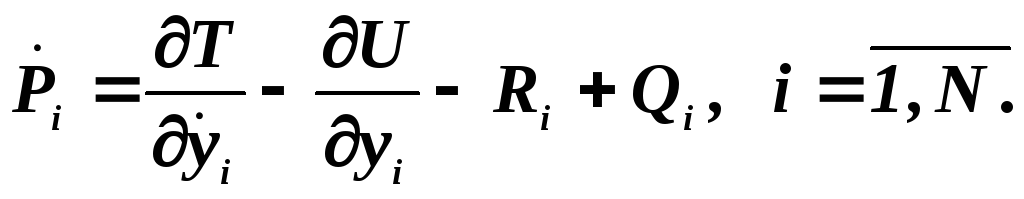
Так как уравнение линейны относительно, то они могут быть разрешены относительно:

В результате уравнения (4.29) приводим к виду

(4.30)

или, вводя новую переменную

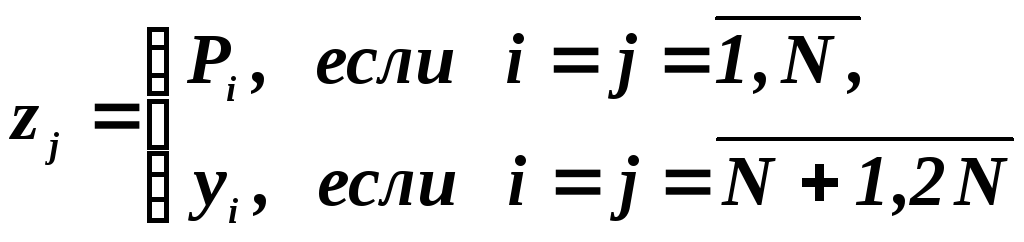
получим

Это выражение можно записать с точностью до обозначений в форме (3.10):

Процедура построения ММ «механической части» САУ на ос­нове формализма Лагранжа состоит из следующих операций:

1) выбор систем координат, связанных с отдельными элемен­тами механической части устройства;

2) выбор обобщенных координат;

3) определение проекций угловых и линейных скоростей эле­ментов механической части устройства на соответствующие оси координат;

4) составление выражений для кинетической и потенциальной энергий и обобщенных сил демпфирования (4.26) — (4.28);

5) определение обобщенных сил Q_t;

6) определение производных в соответствии с уравнением (4.29);

7) составление уравнений (4.29).

Каждую из этих операций можно представить в виде совокуп­ности некоторых операторов.

Подготовка соответствующих выражений для формализма Ла­гранжа «электрической части» устройств САУ сводится к опре­делению контуров электрической схемы (графа схемы), парамет­ры и обобщенные координаты которых используются в дальней­ших исследованиях. Структурой электрической схемы или графом однозначно определяется количество независимых электрических токов (обобщенных скоростей). Общее количество токов в схеме определяется количеством ветвей графа. Количество независимых токов равно количеству независимых контуров. Каждому незави­симому току можно поставить в соответствие свой независимый контур, который в этом отношении соответствует оси координат в механической системе и соответствующей обобщенной скорости.

Сопряжение независимых контуров образует электрическую схему. При подготовке к составлению ММ электрической части нужно придерживаться такой последовательности действий:

1) определить количество узлов схемы;

2) определить количество ветвей;

3) определить количество независимых обобщенных коорди­нат или независимых контуров;

4) выбрать независимые токи, необходимые для исследования;

5) определить конфигурацию контуров так, чтобы контурный, ток был равен независимому току.

Обобщенные силы задаются в виде источников напряжения (если в схеме имеются источники тока, то их надо свести к источ­никам напряжения).