§ 4.3. Упрощение и преобразование математических моделей на эвм

Основная цель при построении ММ — получение ММ, соответ­ствующих целям исследования или выполняемой проектной про­цедуре,— достигается путем упрощения и преобразования полной ММ, построение которой показано в предыдущем параграфе.

Почему же нельзя использовать «полные» ММ непосредствен­но? Полные ММ, как правило, являются избыточными в смысле их применения, они содержат множество «лишних» элементов, за­туманивающих, маскирующих суть дела, дальнейшее их исполь­зование в инструментах САПР приводит к вычислительным слож­ностям, большим расходам средств.

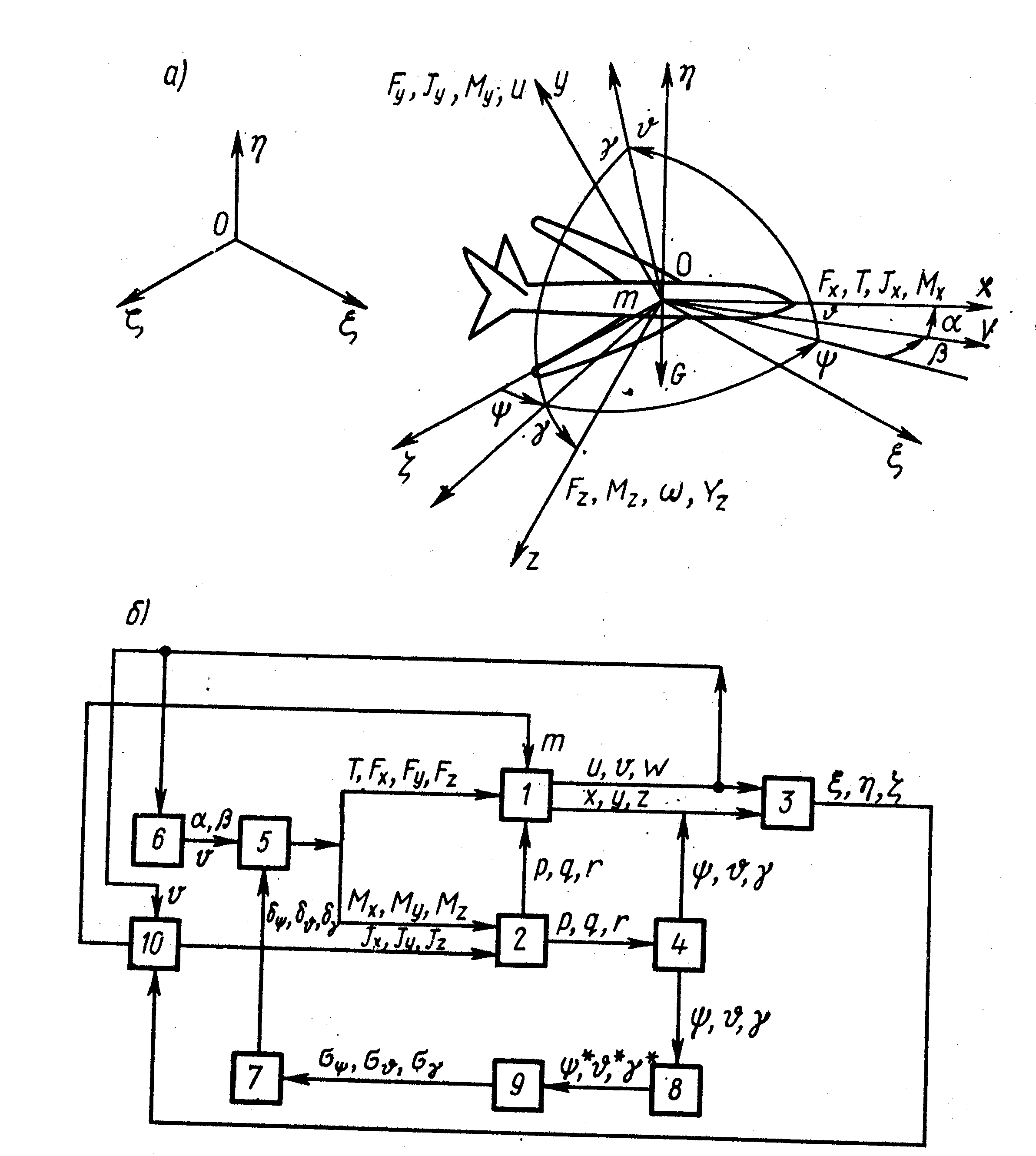
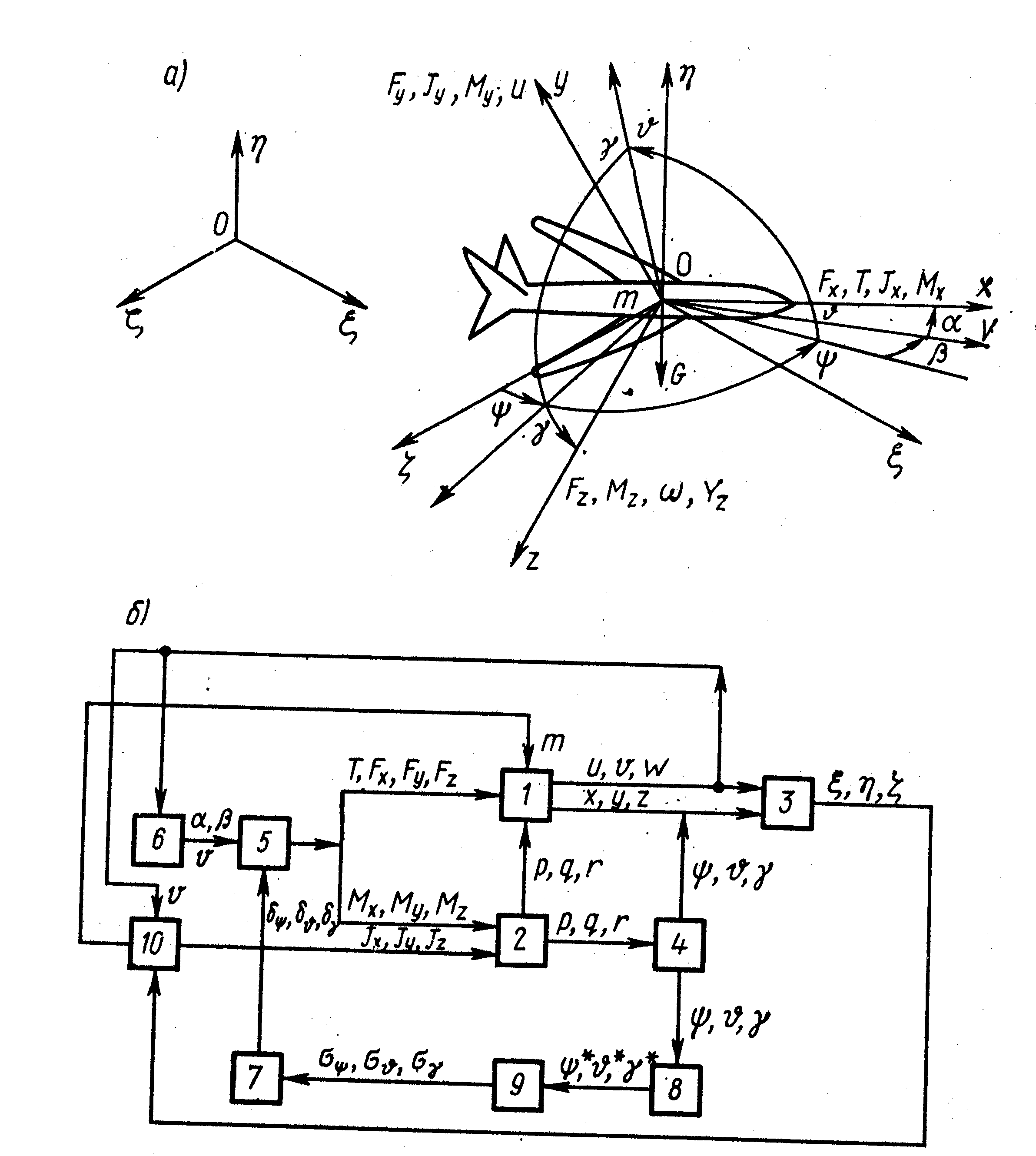
Рис.4.3. Структурная схема «полной» модели ЛА

Например, полные уравнения движения ЛА (рис. 4.3 а) представленные в виде схемы на рис. 4.3б, включают в себя: уравнения линейных перемещений ЛА как твердого тела относительно земной системы координатО, ξ, η, ζв трех взаимно перпендикулярных направлениях под дей­ствием сил тягиТ, аэродинамических силF(F_x, F_y, F_z) в поле тяжести с ускорениемG (блок1); уравнения поворотов относи­тельно центра тяжести в трех направлениях под действием аэро­динамических моментовM(М_Х, M_y, M_z) (блок2); кинематиче­ские уравнения движения центра тяжести ЛА по отношению к земной системе координатξ ,η, ζ(блок3); кинематические урав­нения вращения ЛА относительно центра тяжести на углы крена γ , тангажа ν и курса ψ (блок4); уравнения аэродинамических сил и моментов (блок5); уравнения скорости ΰ, углов скольже­ния β и атаки α ЛА (блок6); уравнения рулевых органов δ_γδ_ψδ_θ(блок 7); уравнения устройств навигации (блок8) и БЦВМ (блок9); уравнения, определяющие изменения массыт и моментов инерции J_x,J_Y,J_z зависимости от потребления горючего (блок 10).

Этот далеко не полный перечень уравнений, соответствующих ММ ЛА, приводит в конечном счете к ММ в виде системы обык­новенных дифференциальных уравнений в форме Лагранжа (3.7) более чем 100-го порядка с несколькими тысячами членов.

В процессе проектирования САУ Л А такой полной ММ поль­зуются только на этапах испытаний всей САУ. Для многих про­ектных процедур расчета, анализа и синтеза САУ применяются упрощенные ММ в формах (3.15), (3.17), (3.16) и др., которые оказываются вполне достаточными для целей этих проектных про­цедур, но неизмеримо проще полной ММ. Так, при предваритель­ном расчете траектории движения центра тяжести ЛА «О», по отношению к земной системе координат ξ ,η, ζрассматриваются уравнения блока 3, а остальные уравнения не учитываются; при расчете динамической устойчивости ЛА исследуются только урав­нения блоков 2, 4, 8, 9, 7, причем с разделением на продольное и и боковое движения соответственно в вертикальной и горизон­тальной плоскости, и т. д.; аналогичные упрощенные ММ приме­няются при проектировании ГСП.

Полная ММ ГСП целесообразна на этапах испытаний ГСП и в некоторых других проектных процедурах, а для большинства расчетных проектных процедур пользуются упрощенными ММ в виде трех несвязанных систем линейных уравнений в формах (3.15), (3.17).

На протяжении «жизненного цикла» проектируемого объекта требуется приводить его ММ в соответствие с непрерывно меня­ющейся информацией об этом объекте, т. е. постоянно решать задачу упрощения и преобразования форм в том или ином объеме.

Под упрощением математической модели в САПР будем по­нимать проектную процедуру П преобразования исходной мате­матической модели М в упрощенную М_i эквивалентную М с точ­ки зрения цели исследования.

Можно выделить следующие основные подходы к решению задачи упрощения ММ.

Редукция:

Исходная модель М последовательно редуцируется к упро­щенным моделям М_iменьшей сложности С (М_i)- Эта процедура предполагает исключение не влияющих на результат исследова­ний и расчетов составляющих ММ.

Декомпозиция:

Здесь, так же как и в (4.32), C(M_i)—некоторая мера слож­ности ММ (порядок системы уравнений, число слагаемых, числоарифметических операций, требуемая память, время счета и т. д.), Операция (4.33) предполагает возможность разбиения исходной ММ на ряд частных моделей. Применительно к задаче упроще­ния ММ это может соответствовать выделению п упрощенных моделей М_i , соответствующих п целям исследования. Ниже рас­сматриваются некоторые методы и вытекающие из них алгорит­мы упрощения ММ.

Ряд алгоритмов строится на основе метода возмущений. Осно­воположником этой группы методов был А. Пуанкаре (француз­ский математик и механик, 1854—1912),. впервые применивший метод возмущений для решения задач теории устойчивости.

Основой метода является положение, что некоторые динами­ческие связи в модели могут игнорироваться, т. е. исходная мо­дель может аппроксимироваться моделью, структура которой проще.

Рассмотрим применение метода возмущений к упрощению первого уравнения системы уравнений (3.15) в случае наличия в ней малого параметра ε>0. Если эту систему можно предста­вить в виде

где А₁₁, a₁₂, А₂₂, В₁, В₂— соответствующие блоки матриц А, В системы уравнений (3.15); Z₁ Z₂— векторы фазовых координат, то, очевидно, сложность ММ и вычислительные затраты при ε=0 сокращаются, так как система распадается на две независимые подсистемы меньшей размерности.

В случае приводимости уравнения (3.15) к виду

(4.34)

при =0 второе уравнение вырождается в алгебраическое, т.е.

(4.35)

Снижение сложности системы (4.35) по отношению к системе (4.34) здесь также очевидно.

Одна из особенностей ММ широкого класса САУ заключается в их нелинейности. Наиболее распространенным методом упро­щения этих ММ является линеаризация (см. систему (3.11)). Во многих случаях линейная модель достаточно хорошо отражает физику работы исследуемой системы, а главное, позволяет при­менить мощный аппарат исследования линейных систем. Кроме того, хорошо известно стремление разработчика строить систему, «работающую» по линейной модели. С точки зрения требуемых аналитических операций при автоматизации этого метода необходимы элементарные подстановки, аналитическое дифференциро­вание, тождественные преобразования.

Ряд преимуществ с точки зрения машинной реализации име­ют методы упрощения, сводящие дифференциальные уравнения к системам конечных, в частности алгебраических, уравнений.

Одним из таких методов является предложенный автором ма­шинно-аналитический метод |[13]. Сущность его сводится к следу­ющему. Пусть ММ задана в форме (3.7), которую представим здесь в виде

где F(Y, Λ, t)= [ f₁(Y, Λ, t), f₂(Y, Λ, t), ..., f_n(Y, Λ, t) ]-задавая в области D вещественная функция от Y, Λ, t; Y(t)=[y₁(t), y₂(t),…, y_n(t)]— вещественная вектор-функция из фазовых координат системы; Λ (t)-=[ λ₁(t) λ₂(t), ..., λ_n(t)] — вектор, составленный из параметров системы, включая входные сигналы и начальные ус­ловия. Полученные . на ЭВМ в результате численного решения системы (4.36) при заданных значениях параметров фазовые ко­ординаты обозначим Y(T). В соответствии с машинно-аналитиче­ским методом (подробнее этот метод будет изложен в гл. 6) функ­ции «машинные решения» исходной системы (4.36) аппроксими­руютсяаналитическими функциями и представляются в виде

(4.37)

где S = (s₁, s₂,…. s_n)—вектор, составленный из характеристик процессов — параметров аппроксимирующих функций φ(t, S) (например, вектор из п, Ω в функциях e^nt, sinΩt, e^nt*sinΩt).

По исходным уравнениям (4.36) и аппроксимациям машинных решений (4.37) в результате определенного процесса последова­тельных приближений .(см. гл. 6) в аналитическом виде получа­ется зависимость

(4.38)

связывающая характеристики процессов в системе с ее парамет­рами. Эта зависимость представляет собой уже конечные уравне­ния, по которым значительно проще, чем по исходным дифферен­циальным (4.36), проводятся исследование и расчет САУ и их устройств.

Уравнения (4.38) могут быть также использованы для упроще­ния исходных дифференциальных (4.3.6) путем их редукции, т. е. исключения, «малозначащих» в смысле цели их применения чле­нов уравнений, параметров. В этом случае по зависимости (4.38),

называемой определяющим уравнением, при условии строится матрица чувствительности характеристик процессов к изменению параметров:

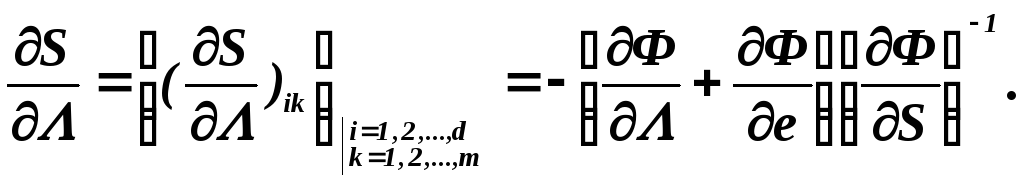(4.39)

Так как параметры САУ имеют различные размерности и значительные диапазоны изменения, то удобнее пользоваться логарифмическими или полулогарифмическими коэффициентами чувствительности и.

В соответствии с матрицей чувствительности (4.39) осуществляется редукция исходной модели (4.36) и построение k-го приближения упрощенной эквивалентной модели

При этом должны быть заданы диапазоны изменения и точность определения каждого из параметров исходной системы и критерий оценки близости исходной и эквивалентной моделей.

В качестве такого критерия выбирается математическое ожидание квадрата разности векторов YиY_е

(4.40)

в течение заданного промежутка времени

На рис. 4.6 приведена схема операций упрощения ММ на ос­нове соотношений (4.36) — (4.40). Приведенные алгоритмы упро­щения реализуются в САПР средствами специального ПОЯ «Упрощение и преобразование ММ» и соответствующего пакета программ*. Перейдем к изложению такого ПОЯ.

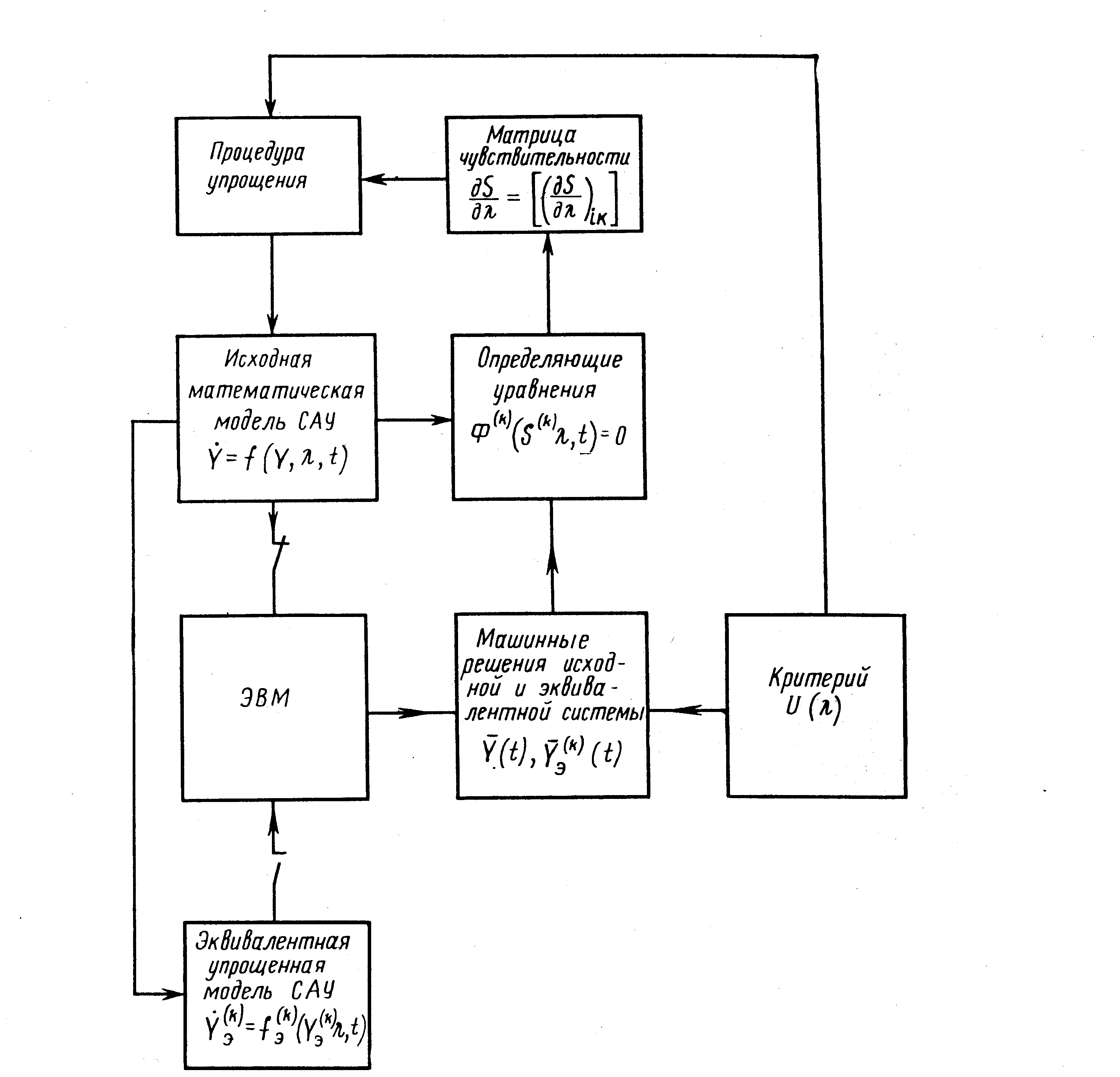
Рис.4.4. Схема операций при упрощении ММ

Программа на ПОЯ «Упрощение и преобразование ММ» пред­ставляет собой последовательность операторов, разделенных точ­кой с запятой. Основным понятием языка является понятие ММ, в качестве которой могут выступать следующие математические объекты:

— системы уравнений — дифференциальные, дифференциально-алгебраические, алгебраические;

— матрицы систем (3.11), (3.15), (3.16), матрица чувствитель­ности (4.39);

— скалярные выражения, т. е. выражения энергий T, U, R в (4.29), характеристический полином (ХП), передаточная функция (ПФ). Первичными объектами являются уравнения, описываю­щие поведение системы и энергетические характеристики. Осталь­ные объекты являются производными от первых.

Большинство операторов такого ПОЯ, выполняющих то или иное преобразование ММ, предполагает следующую структуру: вначале следует действие, обозначающее некую операцию над ММ (построить, привести, ...), затем признак математического объекта (матрица, уравнения, ... )и, наконец, проблемный приз­нак (уравнения чувствительности, передаточная функция ...). Иногда присутствует указание на используемый метод, алгоритм и т. д. Операции могут производиться над некоторой «текущей» ММ.