Алгоритм с перестройкой вероятностных характеристик поиска

В соответствии с алгоритмом, перемещение в пространстве независимых переменных можно записать в виде:

- вектор оптимальных значений переменных за jпредыдущих шагов

- минимальное значение функции качества за jпредыдущих шагов.

Самообучение проявляется в перестройке вероятностных характеристик поиска, т.е. целенаправленного воздействия на случайный выбор направления рабочего шага, т.е. вектор E.

составляющие Е можно определить по зависимости:

- случайное число, равномерно распределенное на интервале ;

Вероятностное воздействие на случайный вектор осуществляется следующим образом:

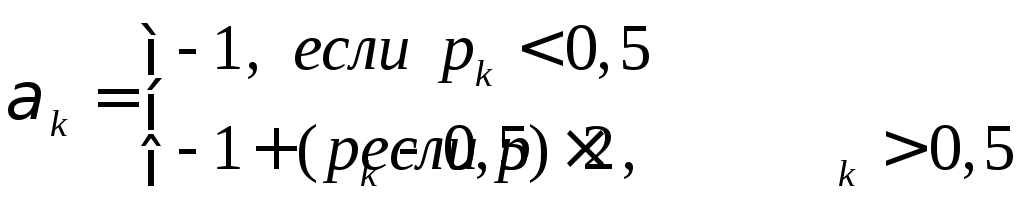
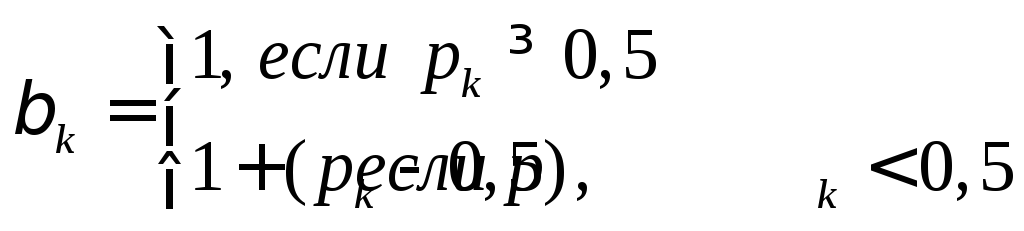
где p_к– вектор выбора случайного шага

Алгоритм обучения реализуется путем изменения параметров памяти при помощи следующей рекуррентной формулы:

- величина, определяющая скорость обучения

- приращение к-ого аргумента на i-ом шаге поиска

Числовые параметры:

; ;

Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов

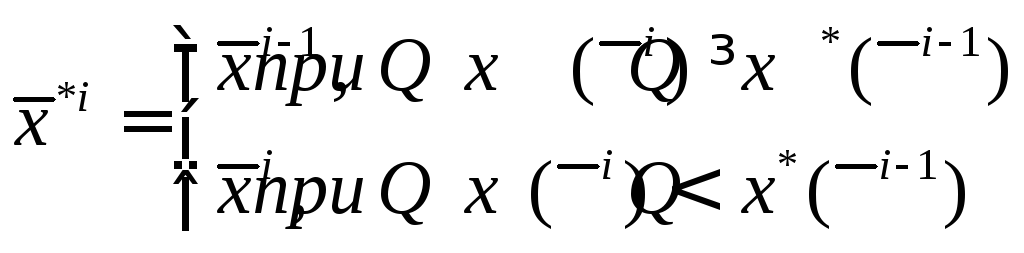
где - этоi-ое пробное состояние выбранное случайно и сохраняемое в памяти в случае удачной пробы

- вычисленное в i-ом пробном состоянии значение функции качества и сохраненное в памяти в случае удачной пробы

Для равномерной плотности распределения пробных шагов, плотность разбивается на «к» этапов, содержащих N_jпробных шагов, где.

Каждый пробный шаг, осуществленный внутри гиперпаралл. пространства независимых переменных , ограничен:

причем стороны гип – да с каждым j-ым этапом уменьшаются в «С», большее 1 раз, по сравнению сj-1 этапом в соответствии с формулой:

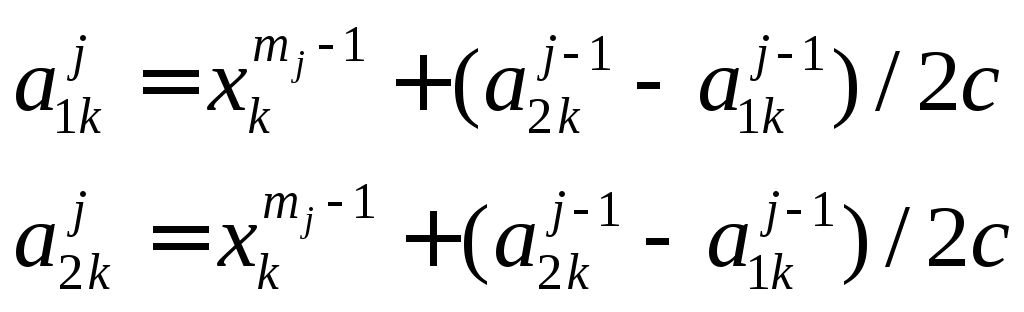
где - точка, соответствующая пробному шагу с наименьшим значением функции качества из всех пробных шагов наj-1 этапе.

Несмотря на равномерную плотность распределения пробных шагов внутри каждого этапа, происходит увеличение плотности распределения от этапа к этапу за счет уменьшения зоны поиска, т.е.

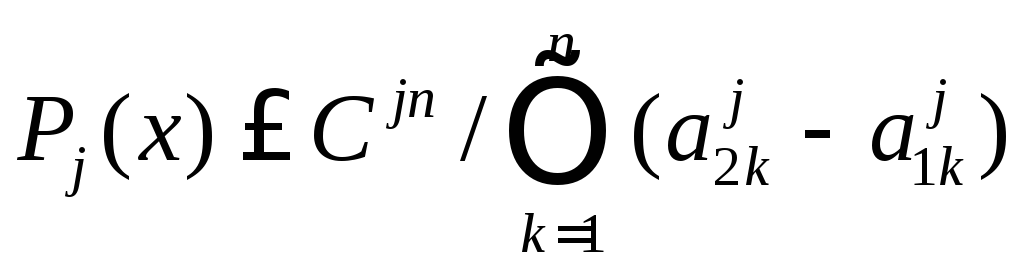
где - плотность распределения пробных шагов наj-ом этапе

- объем гип – да на j-ом этапе

Иногда пробные шаги целесообразно распределять по нормальному закону распределения.

где 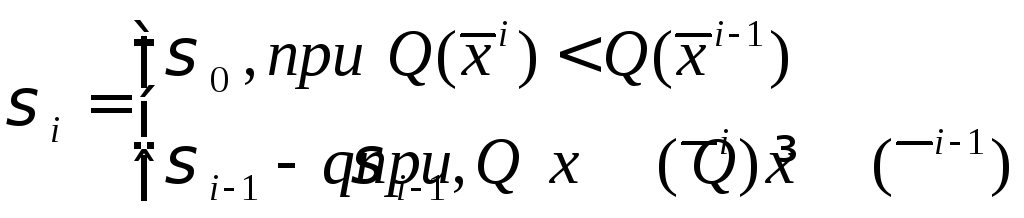при 0<q<1

Итог: Случайные пробные шаги распределены нормально, со средним значением совпадающим с наилучшей величиной критерия качества из всех проб этапа, а дисперсия уменьшается при неудачных шагах и увеличивается до исходного значения при удачных шагах.

Локально – глобальный поиск коллективом автоматов имени Буша – Мостселлера.

Алгоритм осуществляет шаговый поиск.

Выбор знака приращения ∆Хiпроизводится адаптивным алгоритмом, причем алгоритм может работать в двух режимах, причем при переходе на локальный режим надо поменять местами параметры адаптации α и β.

Этапы:

1). Обучение. Обозначим через - вероятность выбора положительного направления поi- ой координате наN-ом шаге поиска.

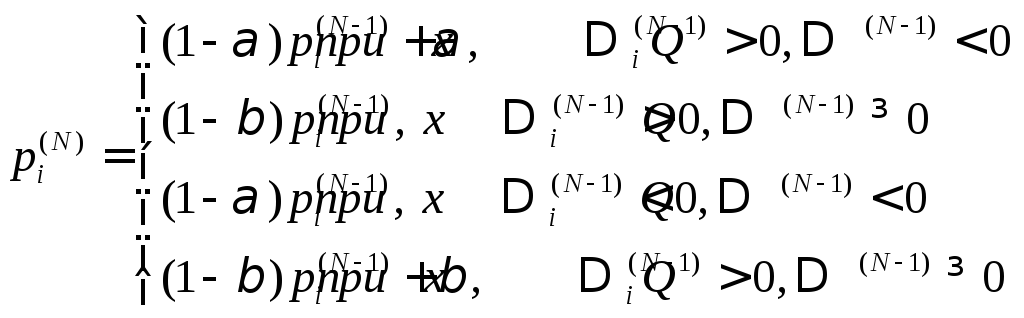(1)

Формула показывает как перестраиваются вероятностные характеристики направления движения к экстремуму.

2). Роль соотношений между α и β:

При α>β поиск имеет глобальный характер – это связанно с тем, что скорость разгона при движении вниз больше чем разгона при подъеме.

При α<β происходит локальный поиск, т.е. торможение преобладает над разгоном и движение напоминает затухающие колебания.

При α=β алгоритм не эффективен, т.е. происходит блуждание в точке минимума без уменьшения размеров этой области.

3). Этап алгоритма: поиск вблизи границы области. Если очередной шаг выводит за границы области, то этот шаг не производится, но адаптация происходит.

Для адаптации используется один из следующих способов:

а) Вероятности обрабатываются по формуле (1) с соответствующими режимами торможения .

б) Производится отражение

(2)

Для глобального поиска способ второй предпочтительнее. Для локального оба равны.

4). Использование ∆Q при обратной связи. После каждого очередного шага обучение производится по формулам (1), однако с переменными α и β, сначала задается α⁽⁰⁾и β⁽⁰⁾. Как правило это максимальное значение. Задается параметр «забывание» δ(0≤ δ ≤1).

После очередного шага α^(N)вычисляется при помощи формул:

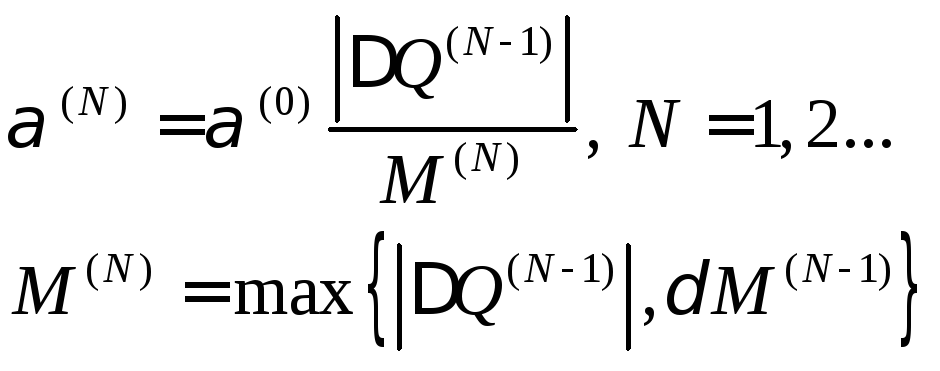(3)

Применение этой процедуры делает адаптацию более гибкой. При β=0, α и β=const.

Исходные данные для алгоритма:

n- размерность пространства независимых переменных

- количество шагов глобального экстремума

k- количество точек, подлежащих локальному уточнению

α и β – параметры адаптации (причем α > β)

γ - коэффициент уменьшения шагов

ε - параметр остановки

- начальное значение независимых переменных и начальные шаги по ним

Алгоритм состоит из этапов:

1. На первых шагах происходит глобальный поиск из данной начальной точкис шагамии с вероятностямиp_i=0,5.

2. В процессе глобального поиска происходит адаптация по формулам, с переменными параметрами, определяемые формулами (3). На границе применяется отражение (2).

3. Результат глобального поиска состоит в определении «k» наилучших точек.

4. После окончания работы глобальной части) производится k– локальных поисков из точек полученного набора, с прежними начальными шагами и начальными вероятностями =0,5.

5. В процессе каждого локального поиска производится адаптация; на границе по формулам (2), внутри области по формулам (1) с параметрами α = α⁽⁰⁾и β= β⁽⁰⁾= начальным.

6. Если при двух последующих двойных подъемах функции качества знаки некоторой переменной были + + - - , - - + +, то шаг по этой переменной умножается на γ.

7. Каждый локальный поиск закончится, когда шаги по всем переменным станут меньше ε.

8. При минимизации текстовой функции

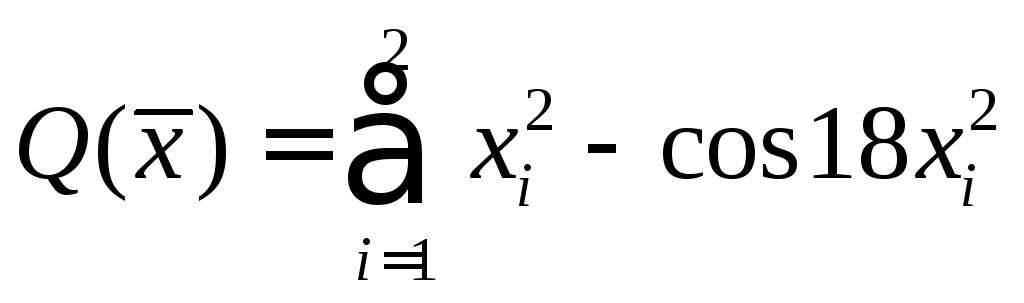- многоэкстремальная, используются следующие параметры алгоритма: