§ 7.2. Машинные методы синтеза

Практическая проверка методов, изложенных в § 7.1, а также других традиционных алгоритмов синтеза показывает, что вычис­лительные трудности не позволяют осуществить сквозной синтез регуляторов САУ по единому функционалу качества с учетом воз­можностей технической реализации и условий эксплуатации САУ. Поэтому предлагается осуществлять синтез изменяемой части САУ в соответствии с процедурой, приведенной на рис. 7.5.

В таком алгоритме последовательно осуществляется синтез структуры регуляторов САУ U = φ(Y, V, К, t) для линеаризован­ных ММ (3.15) неизменяемых их частей при упрощенном функцио­нале качества I_o=I_o(Y, К, V, t) и минимуме ограничений G₀= G₀(Y, Λ, t)≤N_Q и оптимизация параметров САУ машинно-ана­литическим методом (см. § 6.3) уже по полной ММ неизменяемой части Y’=F(Y, Λ, X, U, t) с учетом дополнительных критериев и ограничений

учитывающих характеристики процессов S.

Полученные в результате оптимизации искомые параметры ре­гулятора К и V проверяются при моделировании. Алгоритм яв­ляется итерационным.

В соответствии с представленной на рис. 7.5 схемой синтеза САУ начальным этапом является синтез линейных регуляторов линейных объектов. Стремление получить первое приближение регуляторов САУ в виде, наиболее близком к синтезируемому в смысле критериев (7.8) и (7.9), и охватить как непрерывные, так и дискретные регуляторы САУ приводит к привлечению алгорит­мов методов полиномиальных уравнений (7.16) — (7.19) и частот­ных характеристик.

Однако в ряде случаев эти алгоритмы оказываются практиче­ски неприемлемыми для синтеза многомерных САУ. Этого недо­статка лишены методы пространства состояний (МПС). Они пред­ставляют собой группу машинных методов синтеза САУ на основе формирования исходной ММ в виде (3.15). МПС разработаны в основном для линейных САУ и отличаются от других методов син­теза широкими возможностями по применению ЭВМ для их реа­лизации. В то же время применение МПС для «ручных» расчетов САУ неэффективно.

Создание регулярных методов синтеза на основе представления исходной системы в пространстве состояний еще далеко до завер­шения, и на сегодняшний день существует лишь ряд способов син­теза линейных управлений линейными объектами.

Алгоритмы синтеза регуляторов ряда САУ на основе МПС для различных вариантов задания начальных условий и возмущений приведены в [2, 13].

В тех случаях, когда для синтеза структуры САУ линейные уп­равления оказываются недостаточными для решения задач, по­ставленных перед САУ, приходится осуществлять синтез нелиней­ных регуляторов. В частности, в предыдущих методах не учиты­вается ограничение исполнительных устройств управления. Управ­ления, построенные с их учетом, основаны на замечательной тео­реме выдающегося советского математика Л. С. Понтрягина, по­лучившей название принципа максимума.

В соответствии с принципом максимума для динамической сис­темы (7.36) с функционалом общего вида

Так как «строгий» синтез оптимального управления U(f) при условиях и ограничениях, принимаемых в проектировании САУ, не имеет практического приложения, то для машинной ориента­ции целесообразно воспользоваться квазиоптимальными методами синтеза нелинейных регуляторов. Достаточно эффективной оказы­вается машинная ориентация предложенного Л. Е. Конаревым метода последовательного синтеза управлений, оптимальных по быстродействию. Этот метод позволяет получать управление в ряде САУ, удовлетворяющее критериям (7.8), (7.9).

Сущность метода последовательного синтеза сводится к сле­дующему: исходную систему уравнений (7.36) представим в ска­лярном виде

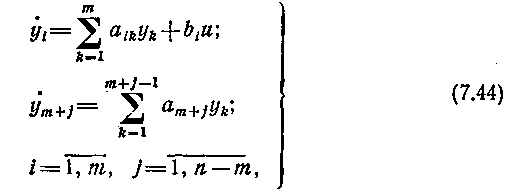
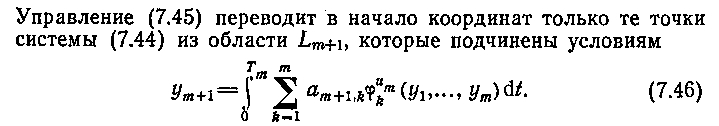
Соотношение (7.46) представляет собой уравнение поверхности переключения системы δ(y₁, y₂, ..., y_т+i) и позволяет строить до статочно полную сетку точек, лежащих на этой поверхности.' Вы­числительная процедура по построению управления (7.45) выпол­няется на ЭВМ. Процедура заключается в получении таблицы точек искомой функции δ(y₁, y₂,..., у_т) с числом входов, на единицу меньшим, чем порядок рассматриваемой системы. Необходимым условием реализации вычислительной процедуры является реше­ние на ЭВМ уравнений движения неизменяемой части системы (7.44).