
- •Часть I р. И. Сольницев
- •Глава 1 Введение в автоматизацию проектирования систем автоматического управления
- •§ 1.1. Системы автоматического управления (сау) как объекты проектирования
- •§ 1.2. Сапр как новые средства проектирования
- •§ 1.3. Этапы истории развития сапр сау.
- •Автоматизация проектирования систем и средств управления
- •Дерево целей проектирования:
- •История развития сапр.
- •Задача векторной оптимизации.
- •Глава 2 процесс проектирования сау и его автоматизация
- •§ 2.1. Цели, критерии и условия ограничений процесса проектирования
- •§ 2.2. Этапы проектирования и проектные процедуры
- •Математическая модель Системы Проектирования (сп) как «спирали проектирования»
- •Глава 3 структура системы автоматизации проектирования сау
- •§ 3.1. Концепция, принципы и их структурная реализация
- •§ 3.2. Техническое обеспечение.
- •§ 3.3. Математическое обеспечение
- •§ 3.4. Лингвистическое обеспечение
- •§ 3.5. Программное обеспечение
- •§ 3.6. Информационное обеспечение
- •§ 3.7. Методическое и организационное обеспечение
- •Глава 4 автоматизация построения математических моделей сау
- •§ 4.1. Методы построения математических моделей и их применение в сапр
- •§ 4.2. Вывод математических моделей в аналитическом виде на эвм
- •§ 4.3. Упрощение и преобразование математических моделей на эвм
- •Математическое обеспечение сапр.
- •Стационарные линейные детерминированные модели систем с сосредоточенными параметрами.
- •Переход от дифференциальных уравнений n – ого порядка к нормальной форме Коши
- •Математические модели элементов сау.
- •Методы линеаризации уравнений
- •Глава 5 моделирование систем автоматического управления
- •§ 5.1. Методы моделирования и их применение в сапр
- •§ 5.2. Приведение математических моделей сау к виду, удобному для моделирования
- •§ 5.3. Численные методы и алгоритмы моделирования
- •§ 5.4. Контроль и оценка точности моделирования
- •Глава 6 автоматизация анализа сау
- •§ 6.1. Методы анализа сау и их применение в сапр
- •6.2§. Машинные методы анализа
- •§ 6.3. Машинно-аналитический метод анализа
- •§ 6.4. Подсистема сапр сау «Анализ»
- •Глава 7 Автоматизация синтеза сау
- •§ 7.2. Машинные методы синтеза
- •§ 7.3. Подсистема сапр сау «Синтез»
- •Методы нлп
- •Задача нлп
- •Градиентный метод оптимизации
- •Метод градиента
- •Метод случайного поиска
- •Метод Даниленко-Каган
- •Метод Трахтенбергп
- •Экстраполяционный случайный поиск с адаптирующимся шагом
- •Алгоритм с перестройкой вероятностных характеристик поиска
- •Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов
- •Локально – глобальный поиск коллективом автоматов имени Буша – Мостселлера.
- •Методика выбора алгоритмов поисковой оптимизации.
- •Метод ситуационного управления:
§ 6.3. Машинно-аналитический метод анализа
Методы третьей группы из перечисленных в § 6.1 разработаны в наименьшей степени, хотя преимущества аналитических форм в смысле общности результатов, удобства и глубины анализа, выявления качественно новых свойств исследуемых САУ вряд ли вызывают сомнения. При решении многих практических задач численный анализ нелинейных САУ на основе моделирования часто оказывается единственным методом. В этом случае обычно пространство параметров разбивают сеткой, а затем в ее узлах производят численное интегрирование системы дифференциальных уравнений, определяющих движение данной системы. Такой способ при исследовании систем большой размерности громоздок и длителен. Выбор путей решения задач анализа значительно облегчается, если получены в достаточно полном объеме зависимости между характеристиками процессов S и параметрами системы Λ в виде некоторых соотношений S = Ф(Λ), При этом желательна именно аналитическая форма таких зависимостей, поскольку появляется возможность перейти от рассмотрения одного конкретного движения к рассмотрению всей совокупности возможных движений в заданной области. Нахождение таких аналитических зависимостей оказывается особенно важным при исследовании САУ ввиду существенной негрубости этих систем, противоречивости и многоплановости задач анализа. Для получения функций S = Ф(Λ) и последующего анализа САУ предложен машинно-аналитический метод, даны его теоретическое обоснование и основные алгоритмы реализации.
Принцип построения этого метода представлен на рис.6.5. Реализация такого метода состоит из следующих этапов:
а) численное решение исходных уравнений движения ММ на ЭВМ – получение машинных решений;
б) аппроксимация машинных решений аналитическими формулами;
в) составление определяющих уравнений, связывающих характеристики процессов с параметрами системы: подстановка аппроксимирующих аналитических формул в исходные уравнения, представленные также в аналитическом виде; алгебраические преобразования;
г) анализ системы по определяющим уравнениям путем реализации соответствующих вычислительных алгоритмов на ЭВМ.

Из определяющих уравнений находятся зависимости между характеристиками процессов и параметрами системы в первом приближении. В случае его недостаточной точности организуется процесс последовательных приближений более высокого порядка. Покажем принципы машинно-аналитического метода на простейшем примере.

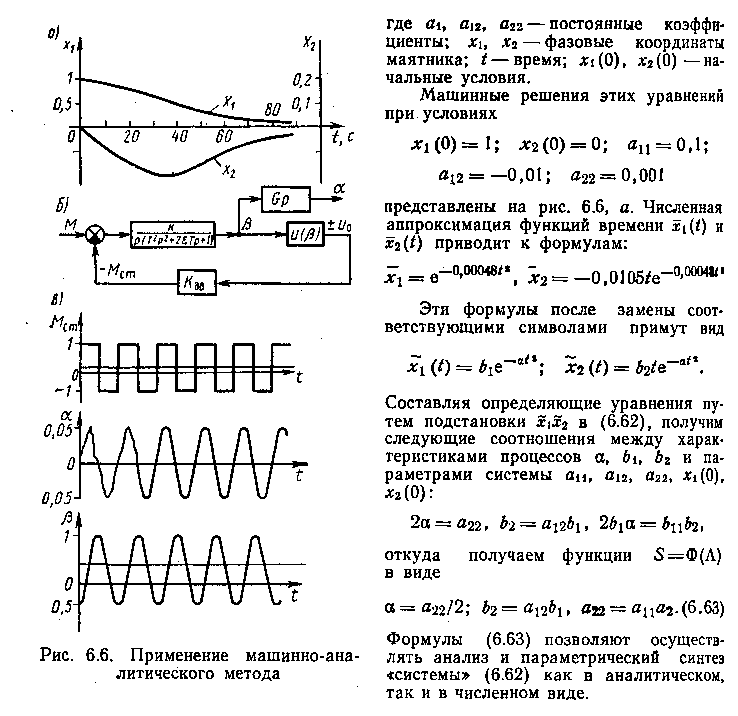
Машинно-аналитический метод при анализе нелинейных САУ позволяет обоснованно выбирать пути решения задач анализа благодаря получению с помощью ЭВМ аналитических зависимостей характеристик процессов от параметров системы типа (6.63). При этом анализ нелинейных САУ сводится, по существу, к анализу этих аналитических зависимостей. Задача параметрического синтеза, традиционно связанная с поисковыми процедурами минимизации функционала, заменяется в машинно-аналитическом методе более простой процедурой решения систем определяющих уравнений, поэтому этот метод положен в основу построения комплекса программ подсистемы САУ «Анализ».
Схема алгоритмизации машинно-аналитического метода для САПР САУ приведена на рис. 6.7.
На первом этапе алгоритмизации по исходной ММ, заданной в форме
![]()
с помощью инструмента «Моделирование» определяется частное машинное решение для заданного набора параметров Л и начальных условий Y0.
На втором этапе осуществляется аппроксимация этого машинного решения. Аппроксимация сводится к последовательному решению таких задач:
— выбор класса аппроксимирующих функций;
— выбор критерия аппроксимаций;
— определение параметров аппроксимирующей функции;
— оценка точности аппроксимации.
При выборе класса аппроксимирующих функций обычно руководствуются видом машинного решения Y (t), простотой выбираемых функций, а также целью их дальнейшего использования.
Собственные и вынужденные движения в САУ — это зачастую процессы, близкие по форме к затухающим или расходящимся гармоническим колебаниям. Учитывая это обстоятельство, а также требования, вытекающие из теории машинно-аналитического метода (независимость, дифференцируемость аппроксимирующих функций, принадлежность их к одному классу вместе со своими производными), аппроксимирующие функции выбирают в классе решений линейных дифференциальных уравнений с постоянными коэффициентами. Поэтому для аппроксимации машинных решений будем использовать обобщенный полином

Аппроксимирующие функции, используемые в процедуре (6.25), (6.26), входят в класс функций (6.65).


Если машинное решение представлено таблицей, дающей n+1 значений Y(t), то дискретный аналог (6.66) принимает вид
![]()
На третьем этапе строятся определяющие уравнения. На выходе блока аппроксимации машинных решений (рис. 6.7) получаем числовые значения параметров обобщенного полинома

Для того чтобы избежать ошибок при составлении системы определяющих уравнений, предусмотрена оценка погрешности приближения. Исходной информацией для контроля служат числовые значения аргументов S* аппроксимирующих функций qN (S*, t). Пусть один из элементов вектора S* считается неизвестным (S1*). Найдем его новое значение (S*1n) путем подстановки в систему (6.70) остальных (S2*, ..., Sn*).
Тогда относительная ошибка δ(S*1, S*1n), полученная в силу уравнений (6.70), позволяет судить о возможности их дальнейшего использования. Если ошибка превосходит некоторое заданное значение, то составляют систему определяющих уравнений во втором приближении. Для получения определяющих уравнений во втором и последующем приближениях разработаны две процедуры.
В первой процедуре (рис. 6.7) точность получения определяющих уравнений связана с улучшением точности аппроксимации машинных решений за счет увеличения числа членов обобщенногополинома. Вторая процедура основана на организации процесса последовательных приближений Ч. Э. Пикара (французский математик, 1856—1941)
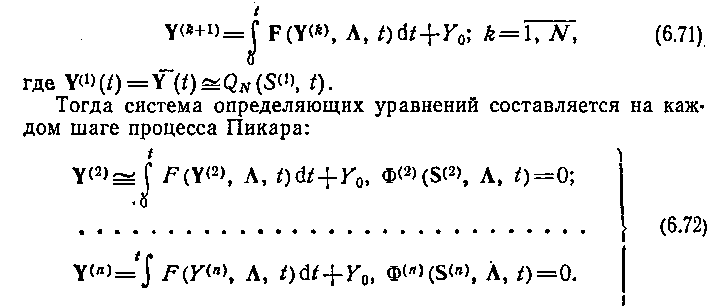
Эта процедура оперирует с исходными аппроксимирующими выражениями qN (S(1), t). Процесс итерации продолжается до тех пор, пока не добиваются удовлетворительной точности δ. На практике этот процесс обычно заканчивается при k=1, 2.
На четвертом этапе по составленной системе определяющих уравнений осуществляется анализ и параметрический синтез исходной нелинейной системы.
В том случае, когда ММ САУ представлена системой дифференциальных уравнений невысокого порядка с одной (двумя) нелинейностями, из системы определяющих уравнений удается найти простые аналитические соотношения, связывающие характеристики процессов с параметрами модели.
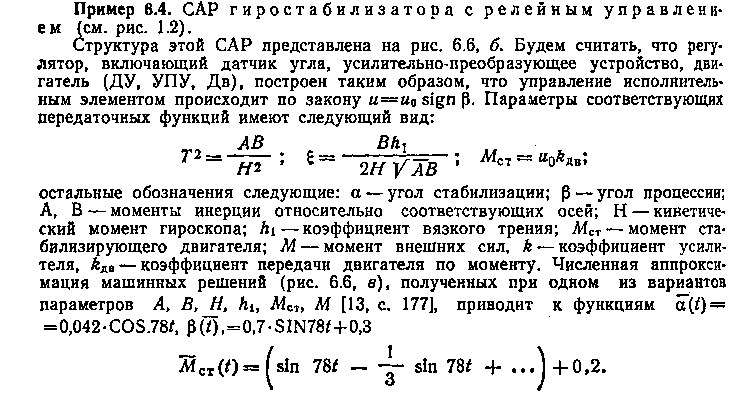

Более общие случаи анализа нелинейных САУ приводят к системе алгебраических и трансцендентных уравнений. Для ее решения применяются итерационные методы. Успешное применение этих методов зависит от выбора начального приближения. Начальным приближением для решения систем определяющих уравнений служат числовые значения S*, полученные в результате аппроксимации машинных решений (6.67). Наличие такого начального приближения значительно увеличивает скорость сходимости итерационных методов и тем самым облегчает весь процесс анализа САУ по определяющим уравнениям.
Существенно упрощается и задача параметрического синтеза, сводящаяся теперь к решению системы определяющих уравнений при заданных в ТЗ показателях на разработку качества системы (характеристик процесса).
Программная реализация машинно-аналитического метода осуществляется на основе компонентов подсистемы «Моделирование»— процедур «Численное интегрирование», «Аналитические преобразования»— и излагаемых далее программных модулей обработки и оптимизации.
