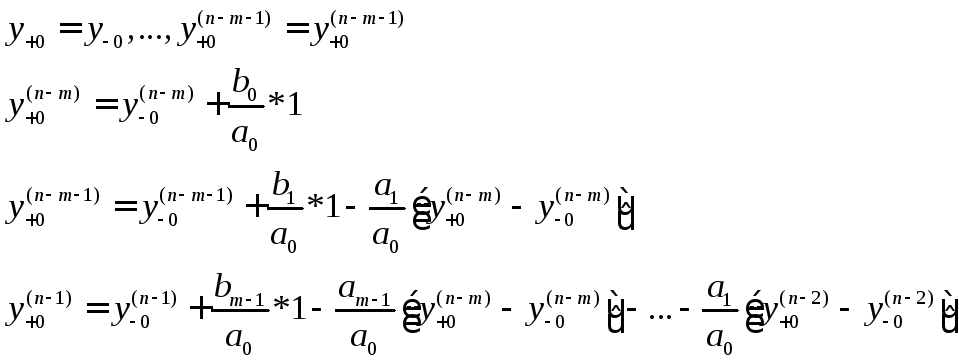- •Часть I р. И. Сольницев
- •Глава 1 Введение в автоматизацию проектирования систем автоматического управления
- •§ 1.1. Системы автоматического управления (сау) как объекты проектирования
- •§ 1.2. Сапр как новые средства проектирования
- •§ 1.3. Этапы истории развития сапр сау.
- •Автоматизация проектирования систем и средств управления
- •Дерево целей проектирования:
- •История развития сапр.
- •Задача векторной оптимизации.
- •Глава 2 процесс проектирования сау и его автоматизация
- •§ 2.1. Цели, критерии и условия ограничений процесса проектирования
- •§ 2.2. Этапы проектирования и проектные процедуры
- •Математическая модель Системы Проектирования (сп) как «спирали проектирования»
- •Глава 3 структура системы автоматизации проектирования сау
- •§ 3.1. Концепция, принципы и их структурная реализация
- •§ 3.2. Техническое обеспечение.
- •§ 3.3. Математическое обеспечение
- •§ 3.4. Лингвистическое обеспечение
- •§ 3.5. Программное обеспечение
- •§ 3.6. Информационное обеспечение
- •§ 3.7. Методическое и организационное обеспечение
- •Глава 4 автоматизация построения математических моделей сау
- •§ 4.1. Методы построения математических моделей и их применение в сапр
- •§ 4.2. Вывод математических моделей в аналитическом виде на эвм
- •§ 4.3. Упрощение и преобразование математических моделей на эвм
- •Математическое обеспечение сапр.
- •Стационарные линейные детерминированные модели систем с сосредоточенными параметрами.
- •Переход от дифференциальных уравнений n – ого порядка к нормальной форме Коши
- •Математические модели элементов сау.
- •Методы линеаризации уравнений
- •Глава 5 моделирование систем автоматического управления
- •§ 5.1. Методы моделирования и их применение в сапр
- •§ 5.2. Приведение математических моделей сау к виду, удобному для моделирования
- •§ 5.3. Численные методы и алгоритмы моделирования
- •§ 5.4. Контроль и оценка точности моделирования
- •Глава 6 автоматизация анализа сау
- •§ 6.1. Методы анализа сау и их применение в сапр
- •6.2§. Машинные методы анализа
- •§ 6.3. Машинно-аналитический метод анализа
- •§ 6.4. Подсистема сапр сау «Анализ»
- •Глава 7 Автоматизация синтеза сау
- •§ 7.2. Машинные методы синтеза
- •§ 7.3. Подсистема сапр сау «Синтез»
- •Методы нлп
- •Задача нлп
- •Градиентный метод оптимизации
- •Метод градиента
- •Метод случайного поиска
- •Метод Даниленко-Каган
- •Метод Трахтенбергп
- •Экстраполяционный случайный поиск с адаптирующимся шагом
- •Алгоритм с перестройкой вероятностных характеристик поиска
- •Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов
- •Локально – глобальный поиск коллективом автоматов имени Буша – Мостселлера.
- •Методика выбора алгоритмов поисковой оптимизации.
- •Метод ситуационного управления:
Математическое обеспечение сапр.
Включает в себя:
математические модели
методы решения задач
алгоритмы
Разработка математических моделей процесс не формальный.
Математическая модель -соотношения, описывающие поведение объекта выведенные на основе законов механики, физики, химических законов и т.д., и удовлетворяющие требованиям точности. Модель должна быть адекватна объекту.
Методы решения –совокупность правил, позволяющих при заданных исходных данных получить нужный результат с использованием выше указанной модели.
Алгоритм-последовательность реализации метода в виде точных шагов которые должна осуществить ЭВМ с целью получения того же результата при заданных исходных данных.
Модели бывают:
макро модели
микро модели
динамические – описываются нелинейными дифференциальными уравнениями
статические - описываются нелинейными алгебраическими уравнениями, либо статическими нелинейными характеристиками. Из нелинейных уравнений можно получить линейные путем линеаризации.
детерминированные
стохастические
И детерминированные и стохастические модели зависят от вида входного воздействия. Стохастические – это когда на систему действует полезный детерминированный или случайный сигнал и случайная помеха.
• стационарные – не зависят от времени
• нестационарные – хотя бы один параметр зависит от времени
• с сосредоточенными параметрами
• с распределенными параметрами
Стационарные линейные детерминированные модели систем с сосредоточенными параметрами.
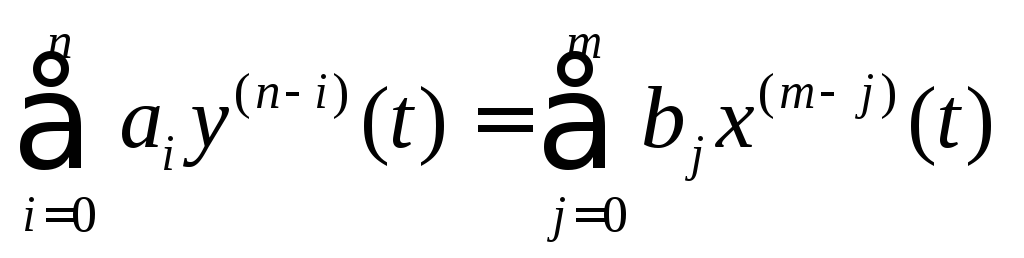 (1)
(1)
Дифференциальное уравнение, которое описывает поведение линейных систем имеет вид (1).
![]() - (импульсная и
переходная) характеристика может быть
найдена путем решения уравнения (1) при
нулевых начальных условиях, при
подстановке
- (импульсная и
переходная) характеристика может быть
найдена путем решения уравнения (1) при
нулевых начальных условиях, при
подстановке
![]() ,
при
,
при![]() .
.
Для определения переходной функции для линейной системы уравнения (1) можно воспользоваться теоремой дифференцирования оригинала при нулевых начальных условиях.
Умножаем на р или рn
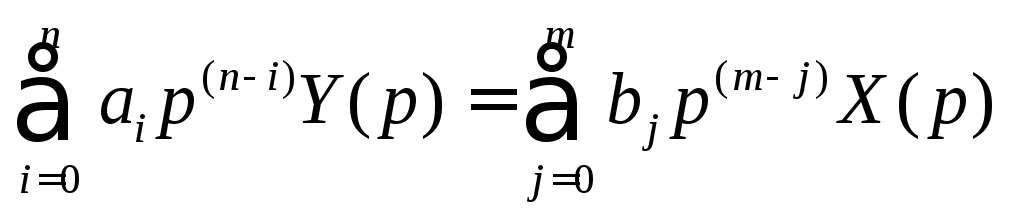
Передаточная функция в виде дробно – рационального выражения;
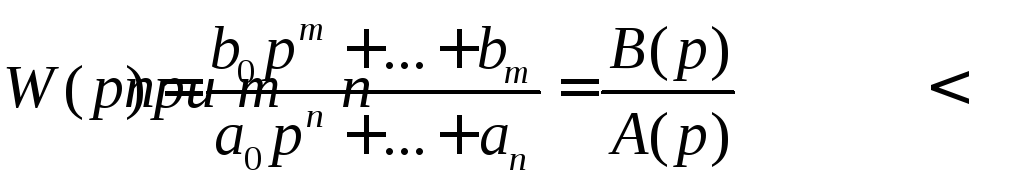
Частотные характеристики, полученные по передаточной функции

![]() *
*

Для осуществления операции * на практике для дробно – рациональной функции вида (3), используют теорему разложения Хевисайда.
Если у нас
 ,
то для такого изображения оригинал
выглядит:
,
то для такого изображения оригинал
выглядит:
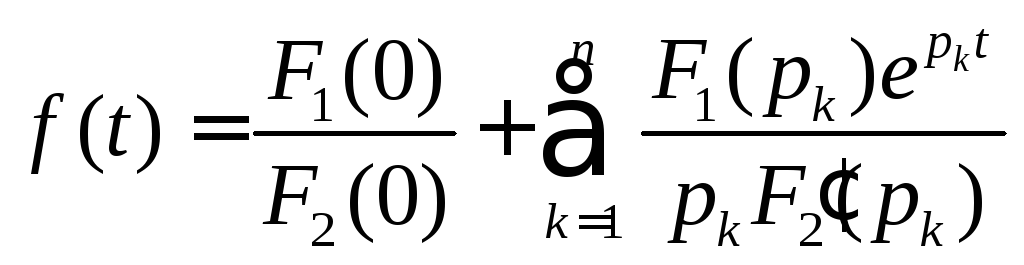
где
![]() - корни
- корни![]()
В том случае, если корни кратные, то формула имеет вид:

Где рк– корни А(р)=0
n– число разных корней
mк– кратность корней рк


Переход от дифференциальных уравнений n – ого порядка к нормальной форме Коши
Дифференциальное уравнение имеет вид:
![]()
![]() -
определение выходной величины
-
определение выходной величины
![]() –промежуточная
переменная
–промежуточная
переменная
Коэффициенты
![]()
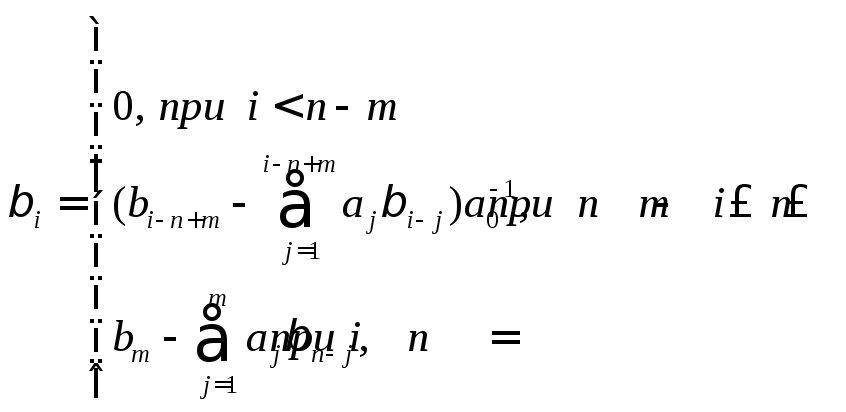
При этом система в форме Коши представляется в виде:
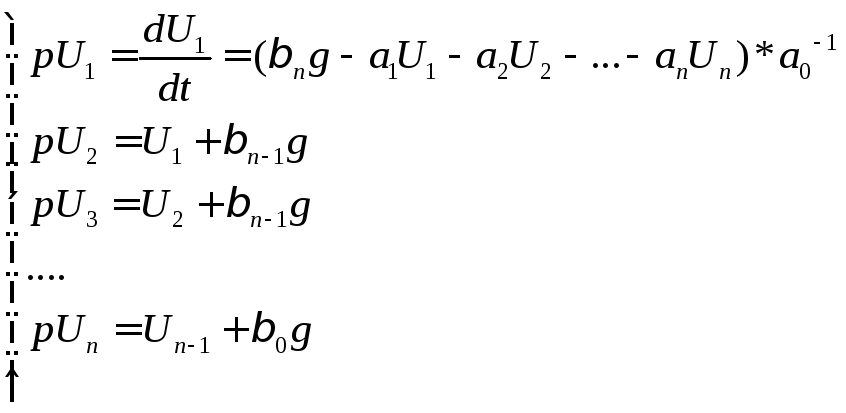
![]() -интересующая нас переменная
-интересующая нас переменная
Эквивалентные начальные условия САР после воздействия на нее 1(t):
Исходное дифференциальное уравнение:
![]()
где
![]() -
единичное ступенчатое воздействие
-
единичное ступенчатое воздействие
![]() –начальное условие
имеющее место перед приложением 1(t)
–начальное условие
имеющее место перед приложением 1(t)
![]() -
начальное условие имеющее место
после приложения 1(t)
-
начальное условие имеющее место
после приложения 1(t)