6.2§. Машинные методы анализа

Применение ЭВМ для изоморфной реализации перечисленных и многих других методов, широко распространенных при «ручных» расчетах, является малоэффективным, поскольку при этом сохра­няются все ограничения, присущие теоретическим методам, и не используются широкие возможности ЭВМ. Анализ состояния воп­роса по разработке второй и третьей групп — специально машин­ных методов — показывает, что их разработка значительно отстает от роста парка и технических возможностей ЭВМ. Разработка теории и практики специальных машинных методов, в полной мере использующих возможности ЭВМ, является новой, чрезвычайно широкой областью исследования.

Специально машинные методы анализа устойчивости линейных стационарных систем базируются на математическом аппарате, исключающем построение характеристического уравнения. В этом случае достигаются экономичность и удобство вычислительной про­цедуры, где отсутствуют неизбежные ошибки округления и от вырождения промежуточных определителей при развертывании оп­ределителя исходной матрицы. Применение этих методов для оце­нок устойчивости «вручную» практически неэффективно.

Общий принцип матричной оценки устойчивости предложен В. И. Зубовым. Алгоритм оценки устойчивости в соответствии с этим принципом сводится к следующему. Пусть однородная сис­тема дифференциальных уравнений имеет вид

На основе предложенного В. И. Зубовым критерия строятся различные матричные алгоритмы анализа качества линейных сис­тем [1].

Применение оценок (6.37) к анализу устойчивости САУ в ряде случаев оказалось затруднительным из-за быстрого исчерпывания ресурсов ЭВМ при перемножении матриц В большой размерности.

Для анализа САУ по переменным состояния (3.15) весьма эф­фективно моделирование на АВМ и ЦВМ на основе принципа па­раллельного воспроизведения нескольких ММ САУ (см. § 5.4). Действительно, в этом случае оказывается возможным одновре­менно и по заданному алгоритму анализировать парциальные со­ставляющие по любой интересующей исследователя обобщенной координате. Существенным достоинством такого анализа является возможность наблюдать и измерять переменные состояния нели­нейных САУ, скрытые от наблюдателя (промежуточные сигналы в цепях САУ, возмущающие механические моменты, перемещения упругих элементов и др.); анализировать влияние изменения пара­метров САУ на их временные характеристики. Так, для анализа качества сложной линейной системы вместо машинно-ориентированных методов можно применить системный метод анализа пар­циальных составляющих, суть которого заключается в следующем. Представим исходную систему (3.10) в виде

Воспроизведя на ЭВМ параллельно системы (6.42) для каждой из составляющих X(t) = {x₁(t), x₂(t), ..., x_m(t),}, строим матрицу парциальных составляющих y_ij(t), j[1,n] для каждого x_it).

По парциальным составляющим y_ij можно провести более глу­бокий анализ исходной системы,, чем классическими методами с известным разделением на устойчивость, качество, точность. В дальнейшем, исследуя выходные координаты y₁, y₂ y₃ ..., у_п при различных возмущениях, получаем исчерпывающую информацию о поведении системы.

К машинным методам с достаточно хорошо отработанными вычислительными алгоритмами относятся методы численного ана­лиза стохастических систем (3.7). Случайные функции, входящие в описание исходной системы, воспроизводятся по их вероятност­ным характеристикам. Для каждой выборки случайных значений интегрируется исходная система уравнений, причем такое инте­грирование производится многократно. Наиболее простую схему имеют алгоритмы, построенные на основе метода Монте-Карло. Этот метод был предложен в конце 40-х годов американскими ма­тематиками Дж. Нейманом и С. Уламом. Само название «Монте-Карло» происходит от города Монте-Карло, знаменитого своими игорными домами. По существу, метод Монте-Карло — это численный метод решения математических задач путем имитации слу­чайных величин. Применительно к ММ САУ (5.32), полученной после приведения (3.7) к виду, удобному для моделирования, схе­му метода Монте-Карло можно представить следующим образом. В исходной системе (5.7)

будем считать, что μ^k= [μ₁^k,..., μ_m^k]—заданные случайные вели­чины, определяемые случайными отклонениями начальных усло­вий и параметров. Выборки значений случайных величин μ^k за­даются с помощью специальных программ для ЦВМ.

Кроме того, задаются функции Ф(S_z), определяющие форму вероятностных характеристик некоторых функционалов от выход­ных координат САУ (математические ожидания, дисперсии, зако­ны распределения вероятности нахождения функции от z(t) в за­данных пределах и т. д.).

Для каждого варианта k значений случайных величин μ^k осу­ществляется решение уравнений (6.43) на ЭВМ. Рассчитываются функции Ф(S_z) в соответствии с интересующими исследователя характеристиками выходных сигналов. Точность статистических оценок по методу Монте-Карло возрастает при увеличении числа N в соответствии с законом «больших чисел».

В соответствии с известными оценками [13] оказывается, что вероятность обеспечения заданной точности метода Монте-Карло δ_N≤ε

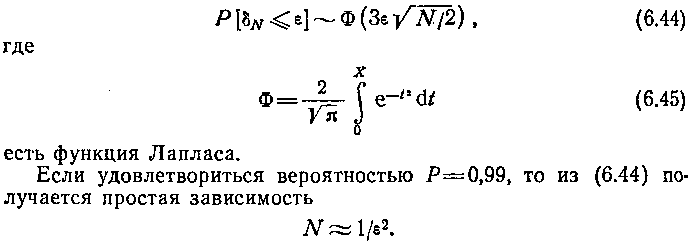
Метод Монте-Карло наиболее эффективно реализуется на аналого-цифровом комплексе САПР САУ по принципиальной схеме, представленной на рис. 6.4. Благодаря возможностям АВМ решать с частотой от 50 до 100 Гц сложные нелинейные дифференциаль­ные уравнения на АЦК принципиально возможно проводить доста­точно полный анализ САУ с высокой достоверностью.

Применение указанных методов для анализа САУ по полным ММ только на ЦВМ становится практически эффективным при использовании системных методов численного интегрирования (5.52).

Частотный анализ можно строить на основе решения задачи Коши. Рассмотрим методы построения ЧХ путем непосредствен­ного вычисления вынужденной составляющей уравнений (3.15) при подаче на выход сигнала x_r=sin ωt.( x_{r принадлежит} x). С точки зрения реа­лизации на ЭВМ такие методы представляются достаточно эко­номичными и удобными, поскольку исключается необходимость вычислений функций комплексной переменной, перехода от исход­ной ММ, записанной, например, в форме (3.15), к передаточным матрицам (6.7) — (6.10), и дополнительных операций из-за учета резонансных и неминимально-фазовых свойств реальных систем.

Применяя методы аналитических преобразований на ЦВМ (см. § 4.3) и системные методы численного интегрирования, можно упростить и ускорить получение ЧХ системы между любыми точками ее структуры как для замкнутых, так и для разомкнутых контуров, а также распространить построение ЧХ для приближен­ной оценки частотных свойств нелинейных систем. Поясним ос­новную идею такого построения ЧХ на системе с одной степенью свободы. Как известно, вынужденная составляющая решения уравнения такой системы

В общем случае системы с п степенями свободы исходные урав­нения для построения ЧХ можно

представить в виде

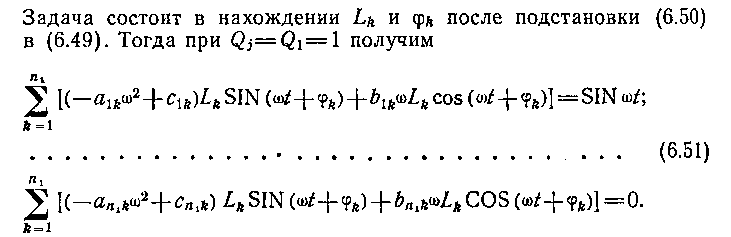
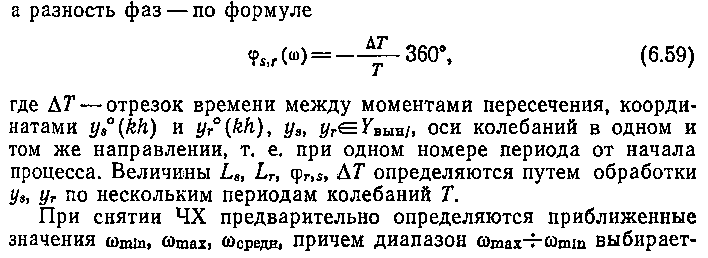
ся в зависимости от целей дальнейшего использования ЧХ. Если это расчет регуляторов САУ, то интерес представляет ЧХ при фа­зовых сдвигах 90—270°; если это исследование динамики САУ во­обще, то надо ориентироваться на диапазон частот, перекрываю­щих изменение фазы от 0 до 360°.

Распространение рассмотренного метода построений ЧХ на не­линейные системы основано на идее гармонической линеаризации нелинейности. В этом случае вместо (6.42) исходная нелинейная система задается в форме (3.10). Строится ЧХ по первой гармо­нике соответствующих составляющих вектора Y. Однако в этом случае уравнения (3.10) следует дополнить двумя скалярными уравнениями фильтров первой гармоники на частоте ω как для входа [y_r(kh)]так и для выхода [y_s(kh)] рассматриваемого уча­стка структуры исследуемой САУ: