3.3. Теплоємність ідеального газу

Теплоємністю тіла С називають фізичну величину, що дорівнює кількості теплоти, яку потрібно надати тілу, щоб підвищити його температуру на 1 К:

. (3.8)

Теплоємність, віднесену до одиниці маси речовини або до кількості молів, називають питомою теплоємністю, або молярною теплоємністю.

; (3.9)

. (3.10)

Виразимо молярну теплоємність ідеального газу, скориставшись формулами (3.1) і (3.10). Для одного моля газу

. (3.11)

У випадку ізохорного процесу pdV_M=0, тому

. (3.12)

Для ізобарного процесу

. (3.13)

Ц

Рис. 3.1. Залежність теплоємності двохатомних газів від температури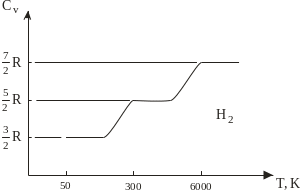

е рівняння Майєра, яке свідчить, що ізохорна й ізобарна молярні теплоємності ідеального газу є різними.

Класична теорія добре описує теплоємність одноатомних газів. Зокрема, ізохорна теплоємність інертних газів (Не, Аr, Xe, Kr), за даними експерименту, справді становить 3/2R і не залежить від температури. Водночас теплоємність двохатомних газів виявляє залежність від температури (рис. 3.1). Цю невідповідність класичної теорії та експерименту пояснює квантова теорія теплоємності, згідно з якою для енергії обертального та коливального рухів складних молекул характерний дискретний спектр:

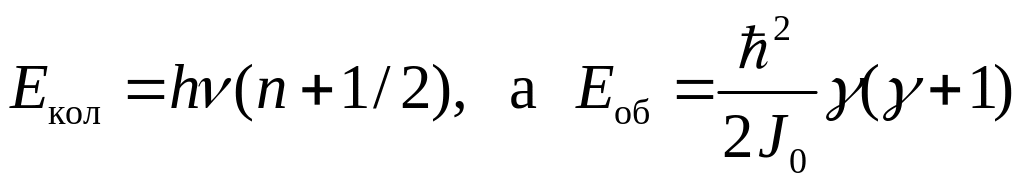, (3.14)

де ν – частота коливань атомів у молекулі; J₀ – момент інерції молекули; ħ – стала Планка; n=0,1,2,3... i j=0,1,2,3... – квантові числа. У квантовій теорії замість статистики Максвелла–Больцмана використовують статистику Бозе–Айнштайна. На підставі (3.14) можна визначити температури, за яких збуджуються коливальні й обертальні ступені вільності молекул:

. (3.15)

Для водню ці температури становлять 85,5 і 5 410 К, відповідно. З погляду квантової теорії ізохорна теплоємність двохатомного газу

. (3.16)

За умови hν>>kТ вираз (3.16) перетворюється в класичний . Отже, квантова теорія повніше описує теплоємність ідеального газу.

3.4. Теплоємність рідин

Теорія, що описує теплоємність газів, незастосовна до рідин, оскільки їхня внутрішня будова суттєво різна. Водночас для рідин, як і для газів, характерні ізохорна та ізобарна теплоємності, однак для рідин . У разі розрахунку – для рідин треба враховувати залежність цих величин від коефіцієнта ізотермічної стисливості і коефіцієнта теплового розширення . Зокрема,

, (3.17)

д

Рис. 3.2. Аномальна залежність теплоємності води від температури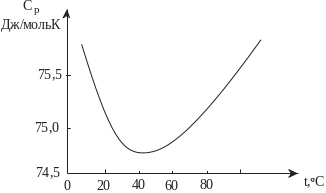

е – молярний об’єм.

Температурна залежність теплоємності рідин неоднозначна і суттєво залежить від їхньої будови та характеру міжмоле-кулярних зв’язків. Результати експериментальних досліджень свідчать, що органічних рідин з підвищенням температури зростає, а одноатомних рідин зменшується. У деяких речовин, зокрема у води, теплоємність з підвищенням температури спочатку зменшується, а потім зростає (рис. 3.2). Сьогодні повна теорія теплоємності рідин ще не розроблена.

3.5. Теплоємність твердих тіл

3.5.1. Класична теорія теплоємності твердих тіл

У 1918 р. П. Дюлонг і А. Пті експериментально визначили, що за кімнатної температури молярна теплоємність одноатомних кристалічних твердих тіл не залежить від їхньої природи і становить 3R. Цей експериментальний факт, який назвали законом Дюлонга і Пті, частково можна пояснити з погляду класичної теорії. Зокрема, класична теорія розглядає кристал як сукупність незалежних атомів-осциляторів, що коливаються з однаковою частотою у вузлах кристалічної ґратки. Оскільки кожен з атомів має три ступені вільності, то енергія його коливного руху становить 3kT, а внутрішня енергія одного моля кристалічної речовини

. (3.18)

Тоді ізохорна теплоємність твердого тіла

, (3.19)

щ

Рис. 3.3. Температурна залежність

теплоємності твердих тіл

о добре узгоджується з законом Дюлонга і Пті. Результати експери-ментальних досліджень завід-чують, що теплоємність більшості твердих тіл за кімнатної темпе-ратури справді близька до 3R, водночас, теплоємність таких речовин, як берилій, кремній, алмаз, бор значно менша від 3R (рис. 3.3). Ці експериментальні факти класична теорія пояснити не змогла. Класична теорія не дає також відповіді на питання, чому зі зниженням температури теплоємність твердих тіл швидко зменшується і прямує до нуля; чому теплоємність металів, у яких, крім ґраткової теплоємності, є ще й теплоємність електронного газу, за кімнатної температури не відрізняється від теплоємності діелектриків і також дорівнює 3R. Як бачимо, експериментальні дані свідчать, що з погляду класичної теорії тут закладені суперечності. Ці розбіжності класичної теорії з експериментальними фактами пояснює квантова теорія теплоємності твердих тіл.