
- •1. Зміст та завдання експлуатації авіаційної техніки.
- •2. Загальні положення щодо організації експлуатації авіаційної техніки
- •3. Організаційна структура підрозділу іас .
- •4. Види контролю авіаційної техніки.
- •5.Бойова готовність та справності ат, шляхи забезпечення.
- •6. Планування і проведення заходів іас по підтриманню а.Т. В справному і боєготовому стані.
- •7. Організація роботи іас по забезпеченню польотів
- •8. Взаємодія іас з атч під час організації і проведення польотів.
- •9. Загальні положення щодо організації та проведення ітп.
- •10.Введення до строю особового складу іас.
- •11.Освоєння нової авіаційної техніки.
- •15. Виникнення та сутність проблеми надійності
- •16. Основні поняття і визначення
- •17. Класифікація відмов.
- •18 . Показники надійності авіаційного рео.
- •Одиничні показники надійності, їх статистичне та імовірносте визначення. Показники надійності не відновлюваних об'єктів
- •Інтенсивність відмов.
- •Показники надійності відновлюваних об'єктів.
- •Математичні моделі безвідмовності.
- •Експоненціальний розподіл часу безвідмовної роботи.
- •2.Нормальний розподіл.
- •3.Пуассонівський потік відказів.
- •2.3 Основні показники ремонтопридатності, довговічності і зберігання.
- •3. Комплексні показники надійності.
- •19. Основні поняття та визначення безпеки польотів.
- •20.Фактори, що впливають на безпеку польотів та надійність авіаційного рео в процесі експлуатації ат.
- •21 .Вплив надійності рео на безпеку польотів
- •22. Аналіз технічного стану рео, шляхи та методи підвищення надійності ат
- •23. Заходи, які запроваджують інженери авіаційної частини з рео по підвищенню рівня його надійності
- •25.Основні види технічної документації іас авіаційних частин.
- •Експлуатаційна документація іас (со).
- •Ремонтна документація іас (со).
- •Облікова та звітна документація іас (со).
- •25.Зміст та постановка завдання теорії масового обслуговування, підрозділ іас як система масового обслуговування.
- •Підрозділ іас (со) як система масового обслуговування.
- •27.Характеристика системи технічного обслуговування з контролем рівня надійності, область застосування.
- •Область застосування технічного обслуговування з контролем рівня надійності.
- •30.Зміст іаз бойових дій.
- •Етапи інженерно-авіаційного забезпечення бойових дій.
- •31. Підготовка ат та авіаційного рео до бойових дій.
- •32. Відновлення бойової здатності ат за результатами бойових дій.
Інтенсивність відмов.
Розглянемо
наступну практичну задачу. Необхідно
визначити ймовірність того, що об'єкт
відмовить на інтервалі
![]() ,
за умови, що на інтервалі
,
за умови, що на інтервалі
![]() він не відказав.
він не відказав.
![]()
Рисунок 4
Як
випливає із самої постановки задачі ця
імовірність
![]() є умовною. Позначимо межу
є умовною. Позначимо межу
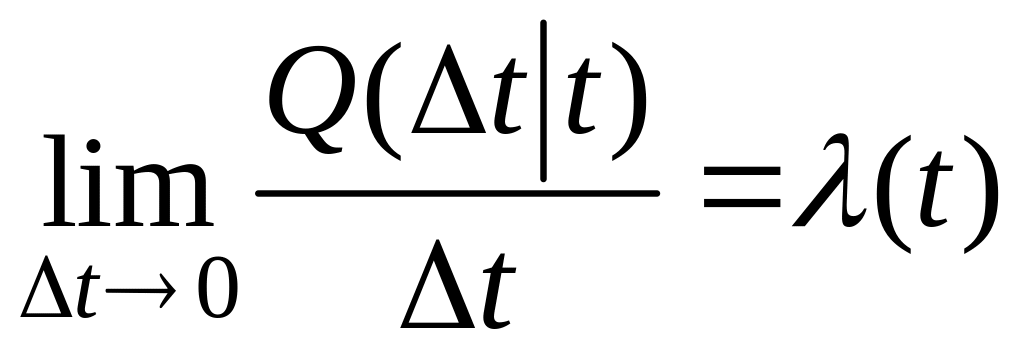 .
.
Тобто є щільність імовірності відказу в момент t за умови, що до цього моменту часу об'єкт працював безвідмовно. Вона називається інтенсивністю відмови. Остаточна формула для має вигляд
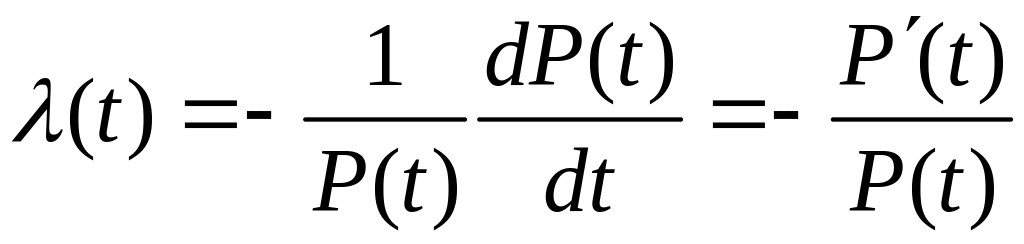 .
.
Проінтегрувавши цей вираз знаходимо
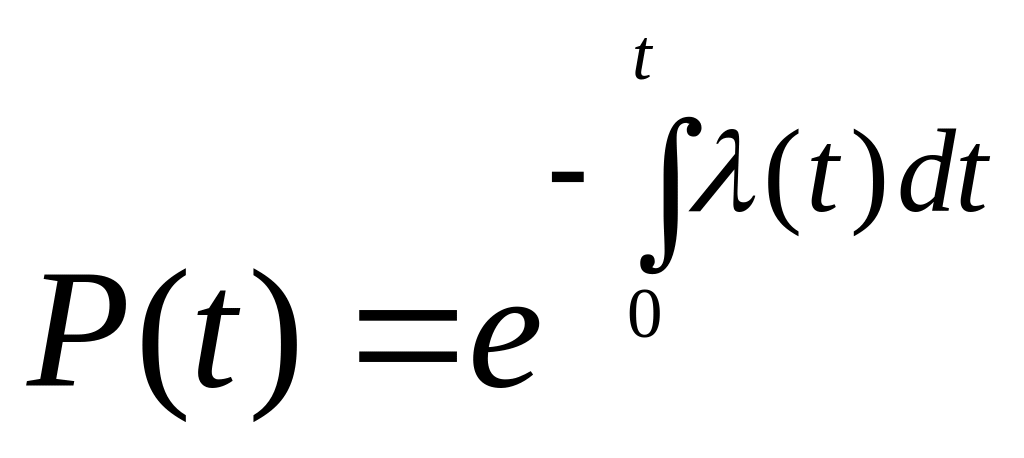 .
.
Цей вираз зветься основним законом надійності.
Таким чином, інтенсивність відказів і імовірність безвідмовної роботи пов'язані взаємо-однозначною відповідністю. Оскільки є функція часу, то в загальному випадку може і не бути експонентою, хоча і виражена через експонентну функцію.
Перейдемо
до статистичного визначення
![]() ,
тобто до визначення
по статистичним даним. Формулу можна
записати у вигляді
,
тобто до визначення
по статистичним даним. Формулу можна
записати у вигляді
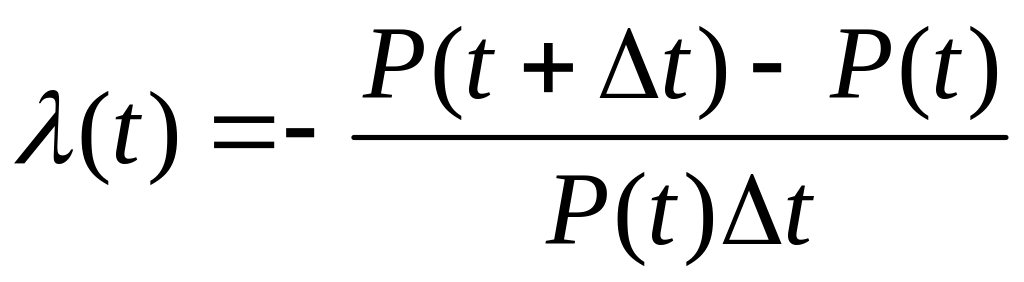 .
.
Підставимо
в неї замість
і
![]() відповідні вираження для
і
відповідні вираження для
і
![]() .
У результаті одержимо
.
У результаті одержимо
![]() .
.
Таким чином, інтенсивність відмов ( статистично) э відношення кількості відмов, що трапилось за одиницю часу, до числа об'єктів, що не відказали до даного моменту. Типова крива залежності від часу експлуатації, показана на рисунку 5.
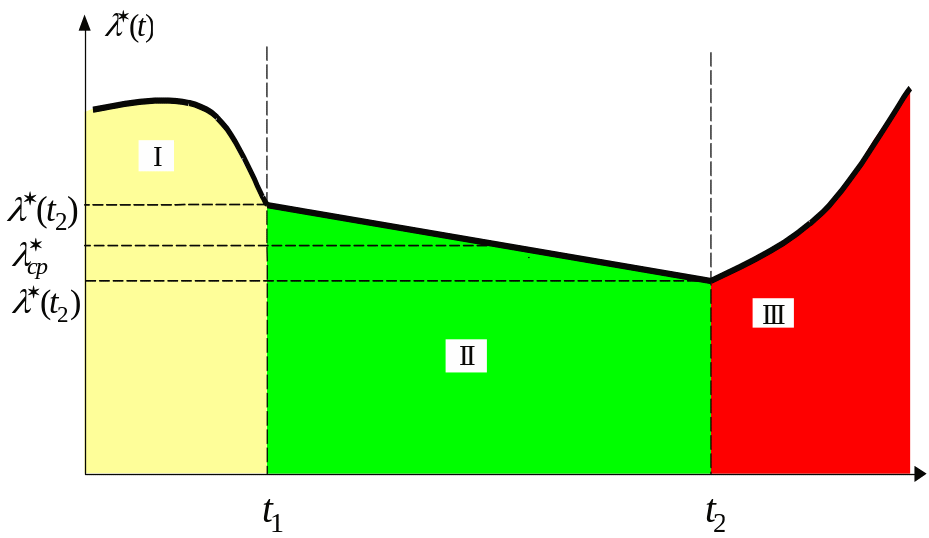
Рисунок 5
На цій кривій можна виділити три характерних ділянки. І – період приробляння, ІІ – період нормальної експлуатації, ІІІ – період старіння.
Звичайно
за період нормальної експлуатації
змінюється мало. Тому вважають, що в
інтервалі
![]() інтенсивність відказів залишається
постійною і рівною
інтенсивність відказів залишається
постійною і рівною
![]() .
.
Крім
того, оскільки
![]() ,
то
,
то
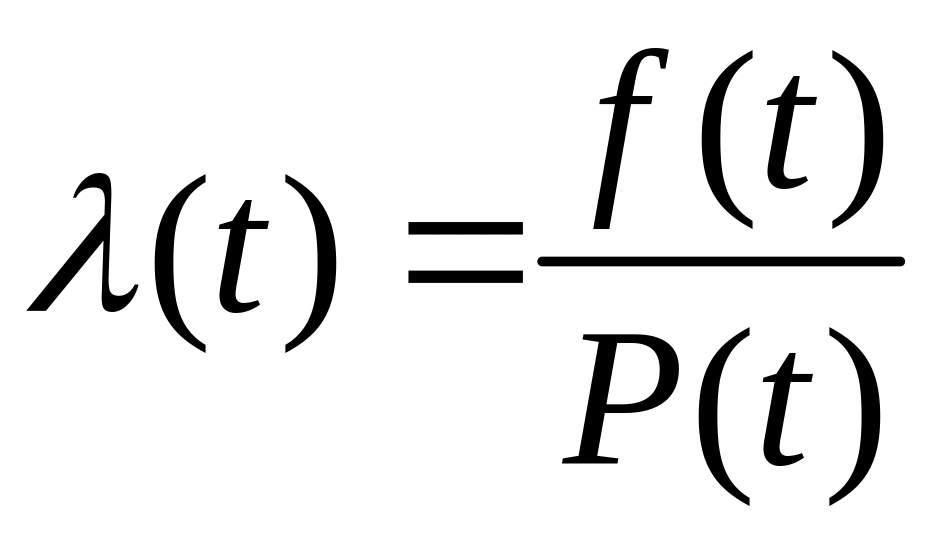 ,
,
Показники надійності відновлюваних об'єктів.
Введені
в попередньому пункті поняття
,
,
,
![]() ,
можуть застосовуватися тільки для не
відновлюваних об'єктів, або для
відновлюваних об'єктів, але тільки до
першого відказу.
,
можуть застосовуватися тільки для не
відновлюваних об'єктів, або для
відновлюваних об'єктів, але тільки до
першого відказу.
Відновлюваний об'єкт характеризується тим, що він експлуатується не до першого відказу, а до вироблення ресурсу. При цьому протягом усього терміну експлуатації об'єкта може виникнути декілька відказів, які після ремонту усуваються.
Розглянемо спрощену модель експлуатації відновлюваних об'єктів
(рисунок 6).
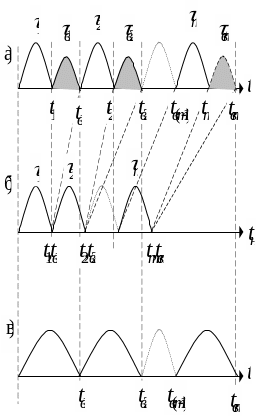 Рисунок
6
Рисунок
6
Об'єкт,
проробивши з моменту початку експлуатації
![]() деякий
час
деякий
час
![]() ,
у момент
,
у момент
![]() відмовив. Потім протягом часу
відмовив. Потім протягом часу
![]() ,
об'єкт був відновлений і в момент
,
об'єкт був відновлений і в момент
![]() він знову почав працювати. У момент
він знову почав працювати. У момент
![]() об'єкт знову відказав і т.д.
об'єкт знову відказав і т.д.
Якщо зобразити процес експлуатації по осі часу наробітку, то моменти відказів і наступного включення збігаються. У такому випадку говорять, що має місце процес миттєвого відновлення.
Випадкові
моменти відказів
![]() утворять послідовність, яку називають
випадковим потоком відмов.
утворять послідовність, яку називають
випадковим потоком відмов.
Випадкові
моменти відновлення
![]() утворять послідовність, яку називаютьь
випадковим потоком відновлення.
утворять послідовність, яку називаютьь
випадковим потоком відновлення.
Показники безвідмовності відновлюваних об'єктів виражаються через характеристики потоку відказів і потоку відновлення.
У теорії надійності за модель потоку відказів прийнято найпростіший потік відказів (Пуассонівскій потік) . Найпростіший потік – це потік, що задовольняє одночасно трьом умовам: стаціонарності, ординарності і відсутності наслідку.
Стаціонарність означає, що кількість відказів на інтервалі часу не залежить від того, де розташовується цей інтервал на осі часу, а залежить від тривалості .
Ординарність означає, що на малому інтервалі малоймовірне виникнення двох і більш відказів.
Відсутність
наслідку
означає, що кількість відказів після
деякого моменту часу
![]() не залежить від того, скільки їх було
до цього моменту.
не залежить від того, скільки їх було
до цього моменту.
Хоча на практиці умови стаціонарності і відсутність наслідку виконуються приблизно, прийнято вважати, що потік відказів об'єктів є найпростішим (для ділянки нормальної експлуатації).
Середнє значення відказів.
Це одна з найважливіших характеристик потоку відказів.
Нехай
маємо
однотипних об'єктів, і
![]() – к-ть відказів i-го
об'єкта на інтервалі
– к-ть відказів i-го
об'єкта на інтервалі
![]() .
Тоді середнє значення відказів
.
Тоді середнє значення відказів
![]() на інтервалі визначається за формулою
на інтервалі визначається за формулою
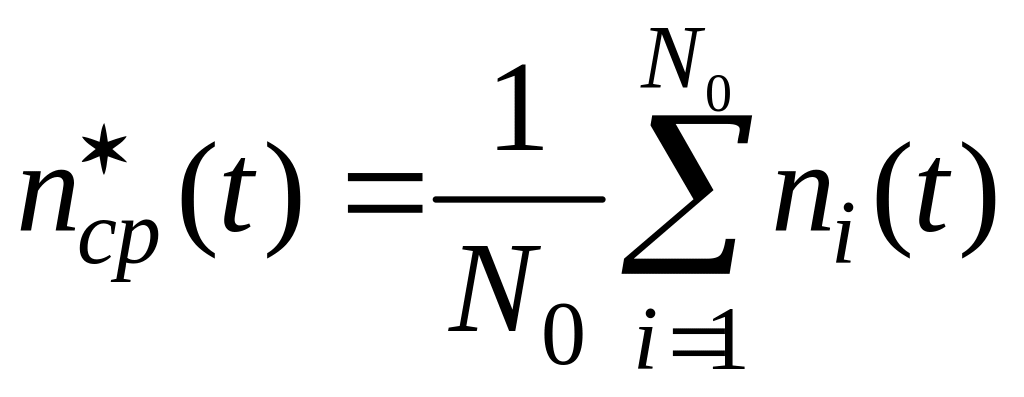 .
.
Ця
величина приблизна. Вона дає оцінку
![]() за результатами обробки статистичних
даних.
за результатами обробки статистичних
даних.
Потік відказів.
Визначений
вище параметр
відноситься до моменту часу t.
Розглянемо момент часу
![]() ,
де
– малий інтервал часу (для дотримання
умов ординарності). Визначимо різницю
,
де
– малий інтервал часу (для дотримання
умов ординарності). Визначимо різницю
![]() .
.
Відношення
![]()
називається
параметром
потоку відказів.
Він характеризує середню кількість
відказів, що відбулися в момент t
за одиницю часу. Тобто, по своїй суті
![]() це диференціальний параметр, що
характеризує швидкість зміни середньої
кількості відказів у будь-який момент
часу. Межа
це диференціальний параметр, що
характеризує швидкість зміни середньої
кількості відказів у будь-який момент
часу. Межа
![]()
Для
нормального періоду експлуатації можна
вважати
![]() ,
тоді к-ть відмов відновлюваних об'єктів
на інтервалі
,
тоді к-ть відмов відновлюваних об'єктів
на інтервалі
![]() .
.
Наробіток на відказ.
Це
найбільш проста і разом з тим широко
використовувана на практиці характеристика
відновлюваних об'єктів. Вона уявляє
собою відношення сумарного наробітку
відновлюваних об'єктів до сумарної к-ті
відказів цих об'єктів за час іспитів
(експлуатації)
t. Тобто, якщо
маємо
однотипних об'єктів і
–
сумарний час наробітку i-того
об'єкта, а
–
сумарний час наробітку i-того
об'єкта, то по визначенню наробіток на
відказ
![]() (середня) дорівнює
(середня) дорівнює
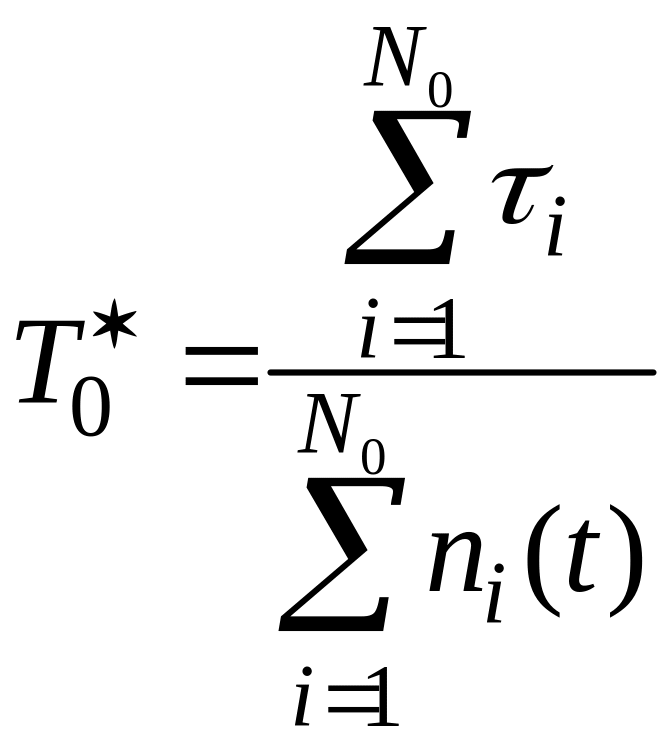 .
(2.2.1)
.
(2.2.1)
Розділивши чисельник і знаменник цього вираження на знаходимо
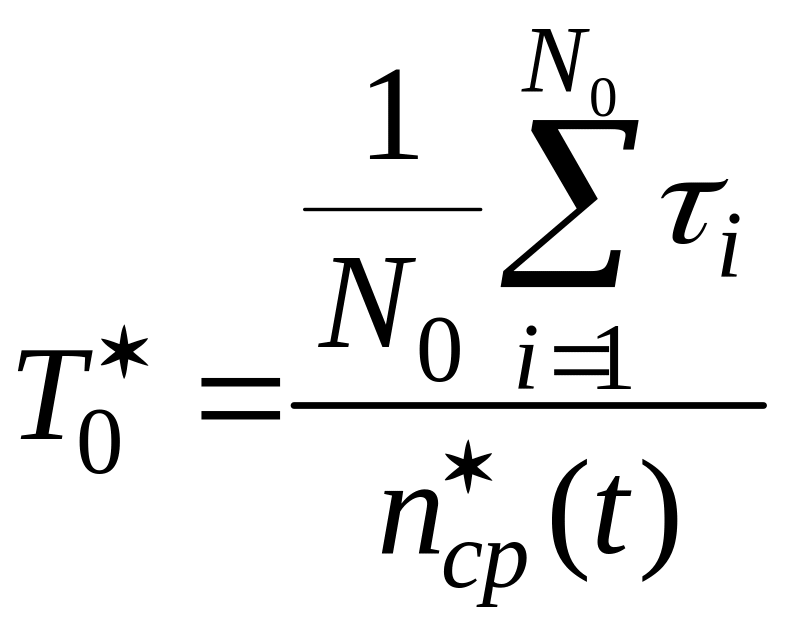 .
.
Чисельник у по суті являє собою середній наробіток відновлюваного об'єкта
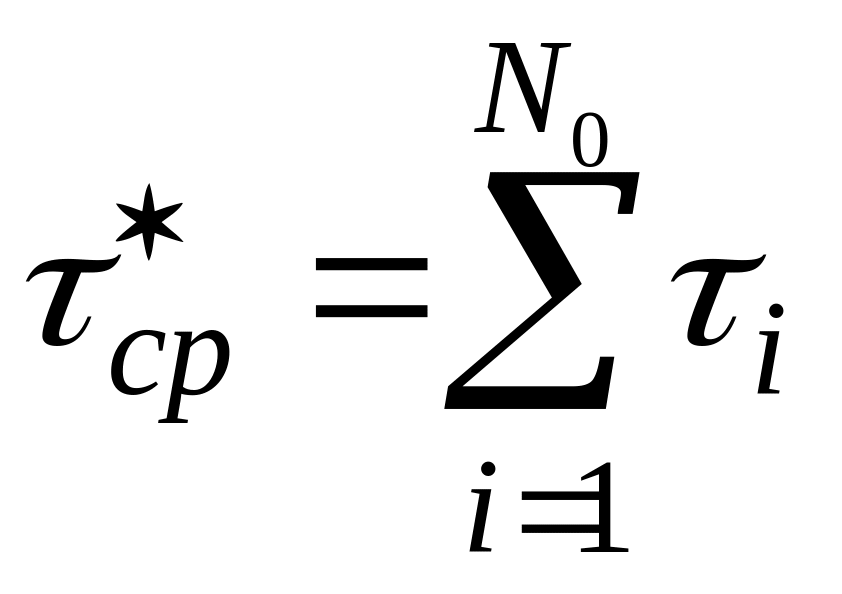 .
.
Отже
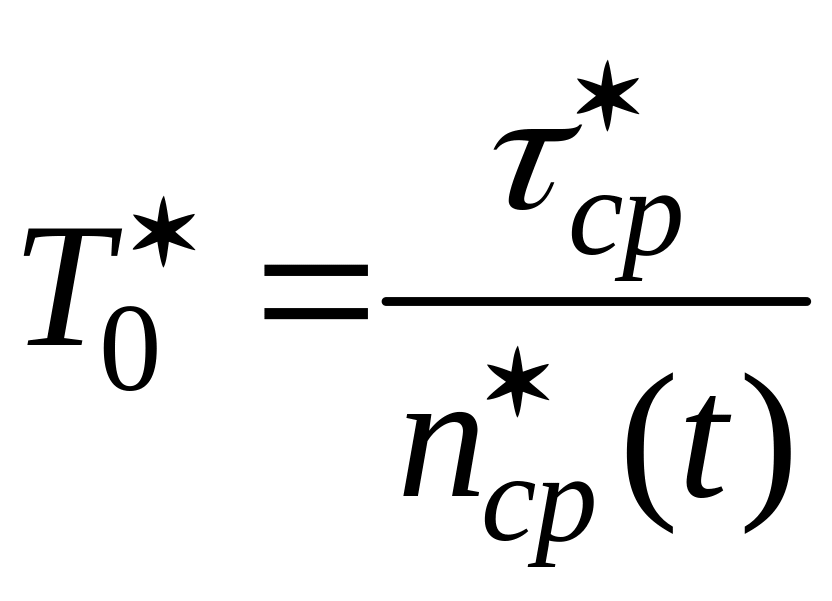 ,
,
тобто – це відношення середнього наробітку до середньої к-ті відказів відновлюваного об'єкта.
