8. Методика введения арифметического корня с натуральным показателем, степени с рациональным показателем
В теме присутствует аналогия с арифметическим квадратным корнем и его свойствами, т.е. это нужно использовать.
Опр
5.
Арифметическим корнем натуральной
степени
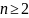из неотрицательного числа
а называется
неотрицательное число, n-ая
степень которого равна а.
.
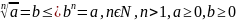Свойства
арифметического квадратного корня
(
:
10.
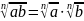
20.
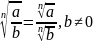
30.
;
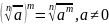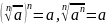
40.
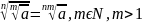
50.
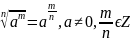
Опр. 6. Корень нечётной степени из отрицательного числа:
.
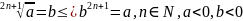Определение степени с рациональным показателем происходит на основе свойства 50:
По
условию m/n
– целое число, т.е. при делении m
на n
в результате получается целое число k.
Тогда из равенства m/n
= k
следует, что m
= kn.
Применяя свойство степени и арифметического
корня, получаем:
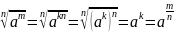
Тогда обращаем внимание, что дробь m/n не всегда является целым числом, т.е. необходимо определить степень с дробным показателем. При этом должны остаться верными все свойства. Вводится соответствующее определение.
Напомним,
что рациональное число r
– это число вида m/n,
где m
– целое, n
– натуральное. Тогда
.
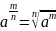Таким образом, степень определена для
любого рационального показателя и
любого положительного основания.
Опр.
7.
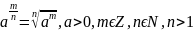
Опр. 1 – Опр. 7 – определение степени с рациональным показателем.
Почему a > 0.
.
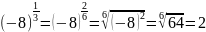−2 = 2 – противоречие.
Показатель степени только положительный.
Если
m/n
> 0, то выражение
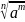имеет смысл не только при a
> 0, но и при а
= 0, причём
.
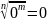Далее доказывается, что все свойства степени с целым показателем верны и для степени с рациональным показателем. Одно свойство доказывает учитель, выделяя теоретический базис, остальные учащиеся сами самостоятельно.
Свойства
степени с рациональным показателем
(
):
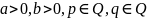10.
20.
30.
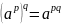
40.
50.
Эти свойства получаются из свойств корней. Докажем, например, свойство
Док-во:
Пусть
p
= m/n,
q
= k/l,
где n
и l
– натуральные числа, m
и k
– целые числа. Нужно доказать, что
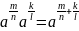
При
ведя дроби m/n
и
k/l
к
общему знаменателю, запишем:
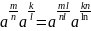
Используя определение степени с рациональным показателем, свойства корня и степени с целым показателем, получаем:
.
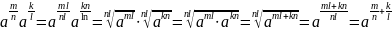Аналогично доказываются остальные свойства.
Опр 1. Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а.
an= a∙a∙… ∙a,
Опр. 2. Степенью числа а с показателем 1 называется само число а. а1 = а
Опр. 3. Если , то:
Опр. 4. Если , то
9. Определение степени с действительным показателем и её свойства
Степень с действительным показателем окончательно вводится в 10 кл. При ответе на вопрос: «Что такое степень с действительным показателем?», нужно говорить: «определение степени с действительным показателем состоит из нескольких определений, перечислим их: Опр. 1 – Опр. 8».
Опр 1. Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а.
an= a∙a∙… ∙a,
Опр. 2. Степенью числа а с показателем 1 называется само число а. а1 = а
Опр. 3. Если , то:
Опр. 4. Если , то
Опр 5. Арифметическим корнем натуральной степени из неотрицательного числа а называется неотрицательное число, n-ая степень которого равна а.
.
Опр. 6. Корень нечётной степени из отрицательного числа:
.
Опр. 7.
Подробнее
поговорим, как вводится степень с
иррациональным показателем. Вспоминаем,
что кроме рациональных чисел нам известны
иррациональные число:
,
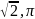0,123… - бесконечная непериодическая
десятичная дробь.
Поэтому
необходимо ввести понятие степени с
иррациональным показателем. Рассмотрим,
как можно определить
.
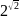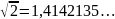
Десятичным
приближением числа
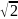по недостатку являются числа:
Т.е.
имеет место последовательность
.
Эта последовательность монотонно
возрастает и ограничена, например,
отрезком [1, 2]. Тогда (по теореме
Вейерштрасса) существует
.
Числа
- рациональные, поэтому для них определены
степени
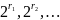Имеем последовательность
.
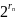В курсе высшей математики доказывается,
что эта последовательность имеет предел
и естественно его считать равным
.
.
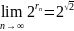Т.е. можно определить степень с любым иррациональным показателем.
Вообще,
пусть a
> 0 и α – произвольное иррациональное
число. Рассмотрим последовательность
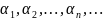десятичных приближений числа α. Эта
последовательность имеет предел
.
Можно показать, что последовательность
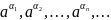также имеет предел. Этот предел обозначают
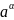и называют степенью число а
с показателем α.
,
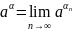a
> 0
Опр.
8.
,
,
.
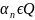Свойства
степени с иррациональным показателем
(
):
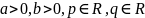10.
20.
30.
40.
50.
Переходим к изучению свойств степени с действительным показателем.
Свойства 10 и 20 не доказываются в рамках школьного курса математики. Свойство 10 достаточно очевидно, а свойство 20 можно открыть рассматривая различные примеры. Отметим, что для степени с действительным показателем сохраняются все известные ранее свойства. Другие свойства доказываются.
Следует подчеркнуть, что рассматриваемые свойства выполняются для степени с любым действительным показателем, а значит, с натуральным, целым, рациональным. Эти свойства будут составлять базу для выявления свойств степенной и показательной функции, для решения степенных и показательных уравнений и неравенств.
Свойства
степени с действительным показателем
(a>0,
a1>0,
a2>0,
):
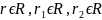10.
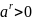
20.
;
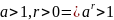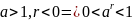
30.
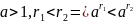
40.
50.
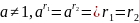
60.
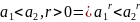
70.
