7. Расширение понятия степени. Методика введения понятия степени с целым показателем

Понятие степени с натуральным показателем вводится в 7 кл.

Опр 1. Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а.

aⁿ= a∙a∙… ∙a,

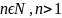
Опр. 2. Степенью числа а с показателем 1 называется само число а. а¹ = а

В выражении aⁿ число а (повторяющийся множитель) называется основанием степени, число n (показывающее сколько раз повторяется множитель) – показателем степени.

Вычисление значения степени называют действием возведения в степень.

Свойства степени с натуральным показателем:

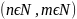
1⁰. При умножении степеней с одинаковыми основаниями, основание остаётся прежним, а показатели складываются.

2⁰. При делении степеней с одинаковыми основаниями основание остаётся прежним, а показатели вычитаются.

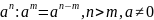
3⁰. При возведении степени в степень основание остаётся прежним, а показатели степеней перемножаются.

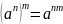
4⁰. При возведении в степень произведения, в эту степень возводится каждый множитель.

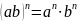
5⁰. При возведении в степень дроби в эту степень возводится и числитель и знаменатель.

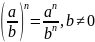
В 8 кл. вводится понятие арифметического квадратного корня.

В 9 кл. проводится расширение понятия степени до степени с рациональным показателем, а затем и до степени с действительным показателем.

Можно использовать аналогию с понятием расширения числового множества, т.е. определение степени на новом числовом множестве не должно противоречить определению степени на предшествующем множестве. Свойства степени, выявленные на предыдущем множестве должны сохраняться на новом числовом множестве, на какое-то свойство должны сниматься ограничения по его использованию.

Существуют разные построения теории действительных чисел. Но можно выделить общую идею. К следующему множеству приходили на основе так называемого принципа перманентности. В соответствии с ним при построении нового, более широкого по сравнению с исходными, множества чисел, операции в нем обобщаются таким образом, чтобы остались в силе законы одноименных действий над числами. Этот принцип уточняется понятием «расширение числового множества». Оно состоит в следующем:

1. Каждое число предшествующего множества входит в последующее множество

2. Все операции для элементов предшествующего множества определены и для элементов последующего множества, причем так они определены, что смысл их сохраняется и в новом множестве.

3. В новом множестве должна выполняться операция, которая была невыполнима им или не всегда выполнима в предшествующем множестве.

4. Расширение одного множества до другого должно быть минимальным из всех возможных.

Учащиеся постепенно должны осознать закон перехода от одного числового множества к другому (Урок обобщения и систематизации)

Мотивацией по введению степени с целым показателем, а затее с рациональным и действительным показателем, может стать решение следующей задачи.

Задача 1. В банках увеличение вклада в зависимости от времени считается по формуле: А_х = А₀(1 + 0,01k)^z, где А₀ – первоначальный вклад, k – количество %-тов в год, х – счётчик времени, А_х – увеличенный вклад за время х.

Пусть А₀ = 100000 руб, k = 6%

Тогда имеем: А_х = 100000∙(1 + 0,06)^х = 100000∙1,06^х

При х = 1 получаем А₁ = 106000 руб

При х = 2 получаем А₁ = 112360 руб и т.д.

Но иногда необходимо узнать значение А_х при х = -1 (т.е. каковым был вклад год назад), при х = ½, х = -2/3, .

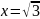От изучения степени с натуральным показателем необходимо перейти к изучению степени с целым показателем, а затем рациональным и действительным.

Задача 2. Важнейшим физическим явлением является радиоактивный распад. Промежуток времени в течение которого распадается половина всех имеющихся атомов вещества физика называют периодом полураспада данного вещества.

Т – период полураспада, t – время, М – начальное количество вещества.

Тогда имеем формулу зависимости количества вещества от времени: . T может быть различное, в том числе и отрицательное (т.е. время до начала наблюдения).

Чтобы сформировать чёткое понимание методологических вопросов, связанных с расширением понятия степени, целесообразно основные результаты изучения каждой темы заносить в канву-таблицу.

Перед введением понятия степени с целым показателем повторяем понятие степени с натуральным показателем и его свойства.

Обращаем внимание, что свойство 2⁰ – деление степеней, справедливо пока только для n > m. Действительно, если 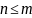, то в правой части показатель степени n – m 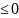. Таким образом, степень с нулевым и отрицательным целым показателем нужно определить так, чтобы данное равенство было верным, как и все остальные равенства.

Пусть n = m, тогда ,

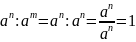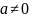
Используем свойство деления (свойство дроби).

Но ,

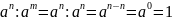Пусть n < m, тогда, например, при n = 2 и m = 7 имеем ,

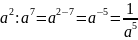Опр. 3. Если 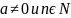, то:

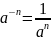
Опр. 4. Если , то

Опр. 1 – Опр. 4 – определение степени с целым показателем.

Далее доказывается, что все свойства степени с натуральным показателем справедливы и для степени с любым целым показателем. Доказательство одного свойства проводит учитель, выделяя теоретический базис, остальные учащиеся доказывают самостоятельно.

Свойства степени с целым показателем:

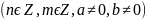
Докажем, например, справедливость равенства при n < 0.

Пусть n – целое отрицательное число. Тогда n = -k, где k – натуральное число. Используя определение степени с целым отрицательным показателем и свойства степени с натуральным показателем, поучаем:

.
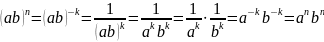