12. Теор. Основы изучения темы «Арифметическая и геометрическая прогрессии»
Особенности и роль темы: Тема «Числовые пос-ти» входит в материал темы «Прогрессии», так как прогрессии - особый вид числовой пос-ти. В шк. курсе математики с помощью пос-тей «открываются» прогрессии. При изучении числовых пос-тей в курсе школы тема «Пос-ти» является вспомогательной и рассматривается лишь в объеме, необходимом для изучения ариф. и геом. прогрессии. Основной целью данного курса является демонстрация посредством пос-тей и их свойств возможностей математики при применении ее методов в физике, биологии, химии, экономике и других науках.
Основные дидактические единицы темы: понятие числовой пос-ти, опр. понятий ариф. и геом. прогрессий, формулы n-го члена ариф. и геом. прогрессий, свойства ариф. прогрессии о среднем ариф-ком и геом. прогрессии о среднем геом-ком, формулы суммы n первых членов ариф. и геом. прогрессий, опр. понятия бесконечно убывающей геом. прогрессии, формула суммы бесконечно убывающей геом. прогрессии.
Нет четкого опр. понятия числовой пос-ти. Числовая пос-ть определяется способом задания (с помощью формулы n-го члена и рекуррентный способ). Опр. ариф. и геом. прогрессий вводятся аналогично. Прогрессиям дается формально-логическое определение: родовое понятие – числовая пос-ть, видовое отличие задается индуктивно. Учащиеся впервые встречаются с опр. такого вида. Для иллюстрации нужно привести историческую справку или пример из жизни, что может послужить мотивацией для изучения данной темы. Учащиеся смогут самостоятельно сформулировать опр. прогрессий, зная, что они являются числовыми пос-тями, и определив предварительно зависимость между членами каждой из них. Кроме словесной формулировки необходимо рассмотреть и символическую запись опр., т.к. в ней отражены рекуррентные формулы, задающие прогрессии.
Также аналогичны свойства ариф. и геом. прогрессий и их док-тва, формулы n-го члена прогрессий и способы их выведения, теоремы о сумме n первых членов прогрессий и их док-ва.
Свойства о среднем арифм-ком и среднем геом-ком доказываются следующим методом: выражаются предыдущий и последующий члены через n-ый член, затем складываются (для ариф. прогрессии) / умножаются (для геом. прогрессии)
полученные равенства, далее выражается n-ый член. Из этих свойств вытекают названия «арифметическая прогрессия» и «геометрическая прогрессия». Учитель должен на это обратить внимание учеников. Важно учителю также отметить, что для каждого из этих свойств справедливо обратное утверждение, а тогда можно сформулировать и критерий, который будем называть характеристическим свойством ариф. прогрессии (геом.прогрессии).
Для ариф. и геом. прогрессий выводятся формулы n-ого члена методом неполной индукции, в которых n-ый член находится через первый член и разность для ариф. / знаменатель для геом. прогрессии. Эти формулы являются ещё одним способом задания прогрессии. Теоремы о суммах n первых членов ариф. и геом. прогрессий доказываются синтетическим методом.
Задачи, приведенные в данной теме с решением в тексте параграфов, являются аналогичными. Правила решения подобных задач не сформулированы. Учитель может их выделить совместно с учениками (чтобы найти требуемое в задаче, можно выписать соответствующую формулу, определить, что в ней известно, а что нет, затем выразить из этой формулы то, что нужно найти, подставив известные значения).
Опр. Числовая по-ть - пос-сть, в которой каждому натуральному числу n ставится в соответствие число an.
Опр. Бесконеч. числовая пос-ть и члены этой пос-ти: а1 – первый член -ти, а2 – второй член пос-ти и т.д., аn – n-ый член пос-и, аn+1 – n+1-ый член пос-ти и т.д.
Опр. Рекуррентный способ задания пос-ти - это такой способ задания пос-ти, при котором пос-ть задается формулой, позволяющей вычислить (n+1)-ый член пос-ти через предыдущие n членов, некоторые из которых задаются доп-но.
Опр. Числовая пос-ть a1, a2, a3,…,an,… называется ариф. прогрессией, если для всех натуральных n выполняется равенство an+1=an+d, где d - некоторое число.
Свойство
о среднем ариф-ком:
«Каждый
член ариф. прогрессии а1,
а2,
а3,…,аn,…,
начиная со второго, равен среднему
ариф-кому двух соседних с ним членов:
.
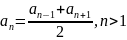Формула n-го члена ариф. прогрессии: аn=a1+(n-1)d.
Сумма
n
первых членов ариф. прогрессии::
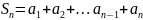
Теорема.
Сумма n
первых членов ариф. прогрессии равна
.
Опр. Числовая пос-ть b1, b2, b3,…,bn,…называется геом. прогрессией, если для всех натуральных n выполняется равенство bn+1=bn*q, где bn ≠ 0, q - некоторое число, не равное нулю.
:
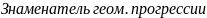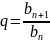
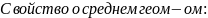«Каждый
член геом. прогрессии b1,
b2,
b3,…,bn,…,
начиная
со второго, равен среднему геом-кому
двух соседних с ним членов:
.
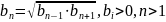Формула
n-го
члена геом.
прогрессии:
Сумма
n
первых членов геом. прогрессии со
знаменателем q≠1:
.
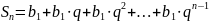Теорема:
«Сумма n
первых членов геом. прогрессии со
знаменателем q≠1
равна
.
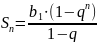Опр. Геом. прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы.
Опр. Суммой бесконечно убывающей геом. прогрессии называют число, к которому стремится сумма ее первых n членов при n, стремящемся к бескон-ти.
Формула
суммы бесконечно убывающей геом.
прогрессии:
.
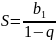Для нахождения разности (знаменателя) арифметической (геометрической) прогрессии пользуются формулой, полученной из определения:
d= an+1-an (q= bn+1/bn, q≠0, bn≠0)
Учебные задачи темы:
1. Формирование представления о числовых пос-тях, о рекуррентном способе задания числовых пос-тей.
2. Формирование представления об арифметической и геометрической прогрессиях как частных случаях числовых пос-ей; изучение их определений и свойств (по аналогии друг с другом).
3. Раскрытие практического значения этих понятий (особенно бесконечно убывающей геометрической прогрессии).
4. Выявление групп взаимосвязанных задач по теме.