30. Методика изучения геометрического смысла производной, уравнения касательной к графику функции

Последовательность изучения геом. смысла производной:

1) ввести определение касательной, как предельное положение секущей

Пусть точки А и М принадлежат графику ф-ии y=f(x). Пусть x и x+h абсциссы точек А и М, тогда их ординаты равны f(x) и f(x+h). Из треугольника АСМ, где С(x+h, f(x)), найдем угловой коэффициент k прямой АМ, который зависит от h. Имеем

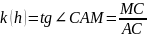
МС = f(x + h) – f(x), AC = h, т.е.

.

П усть число x фиксировано, а h→0, тогда точка А неподвижна, а точка М, двигаясь по графику, стремится к точке А. При этом прямая АМ стремиться занять положение некоторой прямой, которую называют касательной к графику ф-ции y=f(x), потому что lim_(k→0)k(n)) существует и равен f ^|(x). Итак f ‘(x) = tgα.

2) Напомнить, что ур-ние прямой имеет вид: y = kx+b, поэтому чтобы записать конкретную прямую надо найти k и b.

3) показываем, что k = tgα, где α-угол между касательной и положительным направлением оси абсцисс (α – угловой коэффициент прямой).

4) доказывается, что , где x₀ - абсцисса точки касания.

Если y = kx + и – искомое уравнение, то по формуле f ‘(x) = tgα находим k = , т.е. уравнение касательной имеет вид у = .

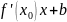5) учитывая, что касательная проходит через точку (x₀,f(x₀)), подставляя их в ур-ие касательной, получим 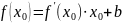, откуда .

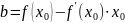Получаем ур-ие касательной: y =

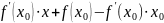
y = – уравнение касательной.

Геометрический смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

31. Теоретические и методические основы изучения темы «Применение производной к исследованию функции»

Необходимо напомнить ученикам, что в начале изучения понятия производной была поставлена задача: Найти средства для исследования функции на свойства и нахождения ее особых точек. «Теперь настала время решить эту задачу. Создается канва таблица и весь материал заносить в таблицу.

Применение производной к исследованию функции
Возрастание и убывание функции …
Экстремумы функции…
Наибольшее, наименьшее значение функции:
На отрезке…	На интервале…

Все теоремы, на которых основаны способы нахождения промежутков монотонности и точек экстремума не могут быть доказаны в школьном курсе математики, но чтобы сделать восприятие учащимися этих теорем более осознанным надо подводить учащихся к соответствующим выводам с помощью графиков. Вспоминаем, какая функция называется возрастающей (убывающей) на промежутке.

Опр. Функция называется возрастающей (убывающей) на промежутке, если она определена во всех точках промежутка, и для любых двух точек х₁ и х₂, принадлежащих этому промежутку, таких что х₁ < x₂, выполняется условие

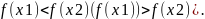
И определения заносятся в канву- таблицу:

Далее рассматривается график функции, который убывает или возрастает на промежутке.

Строим несколько касательных:

1)Угловой коэффициент k>0, значит f ’(x)>0

2)Угловой коэффициент k<0, значит f ’(x)<0

Это выполняется для любого х из (а,b).

Формулируется соответствующее утверждение:

Если f ‘ (x) > 0 на промежутке, то функция возрастает на этом промежутке, если f ‘ (x) < 0, то функция убывает на этом промежутке.

Далее формулируется утверждение обратное данному. Оно доказывается с помощью теоремы Лагранжа. Эту теорему можно показать с помощью графика.

Теорема: Если f(x) непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b), то существует точка с из интервала такая, что f(b) – f(a) = f ’(c)(b – a).

- Пусть функция f(x) непрерывна на [a; b] и дифференцируема на интервале (a,b).

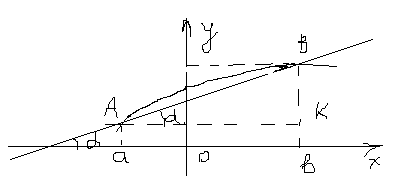
Проведем секущую через точки А (a; f(a)), В (b; f(b)). Тогда угловой коэффициент секущей:

Если будем проводить все возможные прямые параллельные АВ, то найдется такая точка С(с,f (с )), что касательная к данной точке С к графику функции будет параллельна АВ (с принадлежит (а, b)), тогда

f ’(c )(b-a) = f(b) - f(a)- теорема Лагранжа.

Все рассуждения заносятся в канву-таблицу.

Далее рассматривается вопрос нахождения особых точек:

1). вводятся, используя рисунки, определение точки максимума и точки минимума - точек экстремума.

Точка х₀ называется точкой максимума (минимума) функции f(x), если существует такая окрестность точки х₀, что для всех х≠х₀ из этой окрестности выполняется неравенство f(x) < f(x₀) (f(x) > f(x₀))

2). строятся касательные в этих точках, они получаются параллельно оси Ох ( т.е. к=0), тогда f’(x)=0 =>

Формулируется теорема Ферма (если х₀-точка экстремума дифференцируемой функции f(x), то f’(x₀)=0).

3) возникает вопрос верно ли обратное утверждение. Приводим контрпример, что утверждение не верно.

у = x³

f ’(x)=0, но х=0 не является точкой экстремума.

4). Вводиться определение стационарных точек.

Точки, в которых производная равна нулю называются стационарными точками.

Рассматривается особый случай, когда в точке экстремума производная не существует.

Пример: у=│х│в точке х=0 производная не существует, но эта точка является точкой экстремума.

5). Вводится определение критических точек и по рисункам открываем достаточное условие точек экстремума.

Точки, в которых функция имеет производную, равную нулю, или недифференцируема, называются критическими точками этой функции.

На основе изученной теории можно сформулировать алгоритм исследования функции на монотонность и экстремумы:

1)найти производную

2) найти критические точки

3) отметить критические точки на числовой прямой

4) определить знак производной на каждом из полученных промежутков

5) сделать вывод

Далее рассматривается построение графиков с применением производной к их исследованию на свойства. Вводиться схема исследования функции:

1. область определения

2. производная

3. стационарные точки

4. промежутки возрастания и убывания

5. точки экстремума и значение функции в этих точках

Для более точного построения графика обычно находят точки его пересечения с осями координат и, быть может, ещё несколько точек графика.

Обязательно нужно построить график ф-ии, которая рассматривалась на этапе мотивации.

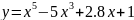
1. Область определения ℝ

2. Функция общего вида, непериод.

3. –

4. –

5. 

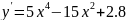
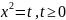
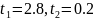
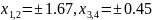
6. Точки 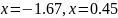- точки максимума, точки 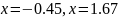- точки минимума

7. –

8. 

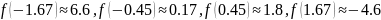
Затем изучается понятие наибольшего и наименьшего значения функции на отрезке, наибольшего (наименьшего) значения функции на интервале. Четко выделяются алгоритм нахождения наибольшего и наименьшего значения на отрезке:

- найти значение функции на концах отрезка, т.е числа f(a) и f(b).

- найти ее значения в тех критических точках, которые принадлежат интервалу (a,b)

-из найденных значений выбрать наибольшее и наименьшее.

В практических задачах функция f(x) имеет на заданном интервале только одну стационарную точку: либо точку максимума, либо точку минимума. В таких случая в точке максимума функция принимает наибольшее значение, в точке минимума – наименьшее значение на данном интервале.

Рассматривая вопрос нахождения наибольшего (наименьшего значения на интервале учитель должен наглядно по рисункам продемонстрировать тот факт, что только наличие единственной точки экстремума на данном интервале позволяет сделать вывод о наличии на интервале наибольшего (наименьшего) значения. Этот факт находит применение при решении текстовых задач.

Тема «Выпуклость графика функции. Точки перегиба» обычно рассматриваются в математических классах.