34. Теоретические и методические основы изучения теории вероятностей в школьном курсе математики 9-11 классов

Фундаментальным понятием теории вероятности (ТВ) является событие и вероятность.

1. Событие.

В ТВ под событием понимается любое подмножество, множество элементарных исходов. Следовательно, для корректного введения определения этого понятия, необходимо, чтобы учащиеся знали элементы теории множеств, но ее изучение в школьном курсе не предусмотрено. Поэтому у учащихся возникает проблема – как здесь поступать? Авторы учебников начинают с рассмотрения простейших вероятностных моделей: подбрасывание игральных костей, извлечение шаров из урны, карт из колоды, стрельба по мишеням. При этом на интуитивном уровне формируется понятие элементарных исходов. Необходимо привлекать исторические сведения. Далее широко рассматриваются такие опыты при любых испытаниях, которых возможны несовместные и равновозможные исходы. Любой такой исход называется – элементарным исходом, или элементарным событием. Затем приводим классификацию событий по степени их возможности реализации: достоверные, невозможные, случайные. С учащимися ведем разговоры о том, что оказывается в окружающем мире и не существует иных событий, кроме этих. Привлекаем примеры из различных школьных дисциплин и окружающего мира.

2. Вероятность.

В настоящее время существует несколько определений понятий вероятности событий: аксиоматический (Колмогоров в 1933), классическая, статистическая и субъективная (на основе экспериментальных оценок). В школьном курсе рассматривается классическое определение: вероятностью события 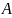называется отношения числа m случаев благоприятствующих событию , к общему числу исходов 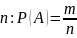. Это определение является конструктивным, т.е. дает способ вычисления вероятности наступления тех или иных случайных событий. Мордкович предалагает эту формулировку в виде алгоритма, т.е. схемы конкретного действия.

Алгоритм нахождения вероятности случайных событий.

Для нахождения вероятности случайных событий при проведении некоторых испытаний следует найти:

1. Число всех возможных исходов данного испытания

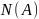2. Количество тех исходов, в которое наступает событие

3. Частное 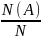– оно и будет равно вероятности события

В качестве примеров определения вероятности событий на основе классического определения вероятности можно рассмотреть задание на вычисление вероятности падения орла/решки при бросании монеты или такую задачу, которая в дальнейшем приведет к открытию теоремы сложения.

Пример: вычислить вероятность того, что при бросании двух кубиков количество выпавших очков будет кратно 4.

Способ 1 (по определению).

Всего элементарных исходов – 36.

– событие, составление в выпадении числа очков кратных 4 ему соответствует 9 элементарных исходов.

По определению 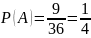этот пример может стать основой для разработки серии упражнений, как для мотивации, так и для формулирования понятия вероятности. Пример: следующее задание на основе данного примера вероятность, какого события выше: выпадение 8 или 9 очков? Вычислите вероятность выпадения очков не больше 5 и т.д.

Однако у классического определения вероятности есть существенные недостатки, оно пригодно только для классических экспериментов, которые редко имеют место в повседневной практике (классический эксперимент – если в результате его проведения реализуется множество событий удовлетворяющих условиям: все события равновозможные, попарно-несовместны и образуют полную группу событий).

Важно, чтобы учащиеся уяснили, что это определение вероятности подходит для очень ограниченного круга явлений и его недостаточно. Возникает необходимость рассмотрения других подходов к определению понятия вероятности и таким подходом является статистический подход, но его изучение не предусмотрено программой по математике (рассматриваются только в профильном классе).

Существует еще одно определение вероятности – определение так называемой геометрической вероятности. Оно применяется в случае, когда есть эксперимент с бесконечным числом исходов и упоминается только в учебниках Мордкович для профильного уровня. К основным теоремам ТВ относятся теоремы сложения вероятностей и умножения вероятностей.

Теорема 1. Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий.

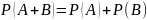
У Мордкович она формулируется в 9 классе, у Калягина в 11, в учебниках есть доказательства. Эта теорема имеет два важнейших обобщения:

1. Верно для любого количества несовместных событий. Об этом в учебниках не упоминается, но у Мордкович есть задача, где этот факт используется.

Пример: в урне лежат 10 белых и 11 черных шаров. Случайным образом достают 5 шаров. Какова вероятность того что:

1. Среди этих пяти шаров ровно 3 белых

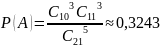
2. Среди них не менее 4х белых шаров

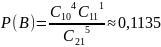
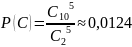
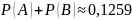
3. Большинство шаров белые

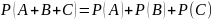
2. Если два события совместны, то вероятность событий 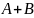: 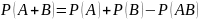вероятность суммы событий равна разности суммы вероятностей этих событий и их произведению.

Формулируется только у Мордкович в 11 классе, есть доказательство. Естественно Мордкович вводит определение произведения событий.

Произведением событий А и В называется событие, которое наступает тогда, и только тогда, когда наступает и событие А, и событие В.

Из теоремы сложения м.б. получено следующее следствие:

1. Сумма вероятности несовместных событий равна 1

2. Сумма вероятности противоположных событий равна 1, т.е. .

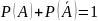Первое следование ни в одном учебнике не обсуждается, второе у Калягина идет как теорема и доказывается, у Мордкович поступают так: на примере конкретных задач поясняется, какое событие называется противоположным и далее говорится, что вероятность события и вероятность противоположного ему события, связана следующим соотношением. .

Для мотивации теорема сложения вероятностей надо рассматривать примеры, которые решаются различными способами (пример тот же)

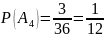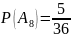Способ 2. По теореме сложения. Всего элементарных исходов 36, выпадает «4» очков – «3» исхода . Выпадает «8» очков – 5 исходов . Выпадает «12» очков – 1 исход

Теорема 2.

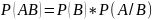
Вероятность произведения двух событий равна вероятности одного события на условную вероятность другого, при условии, что первое событие произошло.

Рассматривается только у Калягина. Сначала на основе конкретных примеров вводится понятие условной вероятности.

Если – два случайных события, которые могут произойти в одном испытании, причем 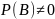, то число называется условной вероятностью события , при условии, что наступило событие 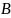, или просто условной вероятностью .

Вероятность события при условия наступления события обозначается 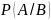, т.е. 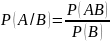из последней формулы выражается

.

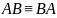
Доказательство не приводится. Для облегчения восприятия теоремы 2 можно поступить следующим образом:

1. На основе примера ввести понятие условной вероятности, т.е. сначала обсудить вопрос о зависимости одних событий от других, дать определение зависимому событию (событие называется зависимым от событий 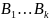, если вероятность события зависит от того, произошли или не произошли события . Если события произошли, то вероятность события вычисляется при этих условиях, называется условной вероятностью и обозначается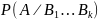 ). Далее рассматривается, иллюстрируется смысл условной вероятности.

Пример: в урне 2 белых и 3 черных шара, определить вероятность того, что 2 последовательно вытянутых шара окажутся разных цветов, если 1 из них белый.

Пусть событие А – оба вытянутых шара разных цветов, В – один из шаров белый. Найдем .

Событий, содержащих хотя бы 1 белый шар,7:б1ч1, б1ч2, б1ч3, б2ч1, б2ч2, б2ч3,б1б2

В качестве мотивации может послужить теорема сложения вероятностей для случая совместных событий.

Возникает мотивация, чтобы найти другую формулу, формулируется теорема 2 в сильном классе ее можно доказывать.

131