
- •2. Простое и необычное множество. Парадоксы и Антиномии. Парадокс Рассела и его роль в математике. Способы избежать Парадокса Рассела. Логические антиномии.
- •3. Операции над множествами и законы алгебры множеств. Диаграммы Эйлера. Формула включений и исключений. Покрытия и разбиения. Классы разбиения.
- •6. Операции над соответствиями. Объединение, пересечение, дополнение, инволюция (обратное) соответствия, композиция соответствий.
- •7. Прямое и обратное соответствие Галуа и его роль в проективном распознавании образов. Свойства соответствий Галуа. Замкнутое подмножество.
- •8. Бинарное отношение. Способы задания. Рефлексивное, симметричное, антисимметричное, асимметричное, транзитивное отношения.
- •10. Диаграмма Хассе как способ задания отношения частичного порядка на множестве. Непосредственно предшествующие элементы. Линейно упорядоченные подмножества.
- •11. Замыкание отношений. Рефлексивное, симметричное, транзитивное замыкание отношений.
- •12. Понятие нечеткого множества. Функция принадлежности и ее интерпретация. Способы формализации нечетких множеств. Наиболее распространенные параметрические функции принадлежности.
- •15. Бинарная операция и ее основное множество. Способы задания бинарной операции. Таблица Кэли. Операционный квадрат таблицы Кэли.
- •16. Свойства бинарных операций: ассоциативность, коммутативность, дистрибутивность, существование нейтрального и обратного элементов, разрешимость уравнений.
- •18. Группоид. Квазигруппа. Латинский квадрат. Лупа. Полугруппа. Моноид. Группа. Абелева группа.
- •19. Подстановки. Композиция подстановок, нейтральная, обратная подстановка. Группа подстановок и ее таблица Кэли. Подгруппы группы подстановок.
- •20. Группа симметрий фигуры.
- •21. Иерархия систем с двумя бинарными операциями: Кольцо. Виды колец. Тело. Поле.
- •4) Аддитивная и мультипликативная операции коммутативны
- •23. Отображения. Изоморфизм. Автоморфизм. Гомоморфизм. Эпиморфизм. Эндоморфизм. Мономорфизм. Биморфизм.
- •25. Способы задания графов: матрица смежности, матрица инциденций и список смежности.
- •28. Алгоритм определения компонент связности в неориентированном графе.
- •29. Эйлеров путь в графе. Эйлеров цикл. Теорема о существовании эйлерова цикла. Алгоритм нахождения эйлерова цикла и его вычислительная сложность.
- •33. Необхдимое и Достаточное условия для определения дерева. Задача построения минимального остовного дерева. Алгоритм Краскала. Алгоритм Прима. Оценка вычислительной сложности.
- •35. Алгоритм нахождения кратчайшего расстояния от источника до всех верши в общем случае – алгоритм Форда-Беллмана. Сложность алгоритма
- •36. Алгоритм Дейкстры — алгоритм нахождения кратчайшего расстояния от источника до всех верши в случае неотрицательных весов. Сложность алгоритма.
- •37. Лемма о перенумерации вершин. Алгоритм перенумерации вершин графа.
- •38. Алгоритм нахождения кратчайшего расстояния от источника до всех верши в случае бесконтурных графов. Сложность алгоритма.
- •39. Система pert. Алгоритм топологической сортировки. Критический путь и способ его нахождения.
- •41. Потоки в сетях. Классификация вершин по воздействию на поток. Величина потока. Разрез и поток через разрез. Теорема о максимальном потоке. Метод увеличивающих цепей.
- •42. Знаковые орграфы и задачи социологии. Теорема Харари о балансе. Недостатки математической модели о балансе.
- •45. Эквивалентность и включение сетей Петри. Построение дерева достижимости сети Петри.
- •46. Виды сетей Петри: временная, стохастическая, функциональная, цветная, ингибиторная. Использование сети Петри для проверки абстрактного сценария. Сеть Петри для задачи об обедающих философах.
- •48. Основные схемы логически правильных рассуждений.
- •51. Формы записи формул (функций) — инфиксная, префиксная, постфиксная. Преобразования формул: инфиксная в префиксную и постфиксную, префиксная в инфиксную, постфиксная в инфиксную.
- •52. Элементарная конъюнкция, элементарная дизъюнкция. Днф, сднф, кнф, скнф. Построение сднф и скнф по таблице истинности. Преобразования днф в сднф. Преобразование кнф в скнф.
- •53. Полиномы Жигалкина. Построение полиномов Жигалкина.
- •54. Классы логических функций: сохраняющие 0, сохраняющие 1, монотонные, линейные, двойственные, самодвойственные. Критерий поста.
- •55. Упрощение сднф при помощи Карты Карно. Булева алгебра и коммутационные схемы. Анализ и синтез коммутационных схем. Проектирование полубитного сумматора.
- •56. Функции k-значной логики и их задание с помощью таблицы истинности и таблицы Кэли. Примеры k-значных логик: алгебра Вебба, алгебра Поста, алгебра Россера-Тьюкетта.
- •59. Квантор всеобщности и квантор существования. Область действия квантора. Связанное и свободное вхождение переменной в формулу.
- •61. Эквивалентные соотношения логики предикатов. Префиксная нормальная форма. Процедура получения пнф.
- •62. Конечный автомат. Способы задания: таблицей, диаграммой.
- •64. Виды автоматов: Мили, сильносвязанный, автономный, Мура. Изоморфизм и эквивалентность автоматов. Изоморфизм графов и автоматов. Неотличимые автоматы. Минимальный автомат.
- •65. Подстановочные, перестановочные криптограммы, Шифр Тритемиуса.
- •66. Равномерные коды, неравномерные однозначно декодируемы (префиксные) коды: код и дерево Фано, кодирование и дерево по Хафменну.
- •67. Условие однозначной декодируемости для неравномерных кодов.
- •69. Кодирование и декодирование по Хеммингу.
41. Потоки в сетях. Классификация вершин по воздействию на поток. Величина потока. Разрез и поток через разрез. Теорема о максимальном потоке. Метод увеличивающих цепей.
Пусть
G = (V,
E) — связный граф и F
E —
подмножество множества его ребер. При
этом F называется
разделяющим множеством если подграф
G
= (V, E
– F) несвязен. Разделяющие
множества всегда сущ. (если в графе
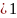 вершины), т. к. всегда можно положить F
= E. Разделяющее множ.
Может разбить граф на 2
и больше компонент.
вершины), т. к. всегда можно положить F
= E. Разделяющее множ.
Может разбить граф на 2
и больше компонент.
Если задан связный граф G = (V, E) и множество его вершин разбито на 2 непустых подмнож. W и множество ребер, соединяющих W с W, называется разрезом. Для любого множества W это множество ребер будет непусто в силу связности графа G, поэтому разрез определен.
Сеть — пара S = G, с, где G = V, E — произвольный орграф, а с: E R — функция, которая каждой дуге u, v ставит в соответствие неотриц. вещественное число с(и, v), называемое пропускной способностью этой дуги. Множества V и Е называются соответственно множеством вершин и множеством дуг сети S.
Под разрезом Р(А) сети S, соотв. подмнож. А V (А , А V), мы понимаем множество дуг u, v Е, таких что u А и v V\A, т. е. P(A) = E (A (V\A)).
Для
произвольного потока f в сети S
поток через разрез Р(А):
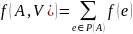 .
.
Определим
пропускную способность разреза Р(А)
следующим образом:
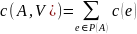 .
.
Под минимальным разрезом, разделяющим s и t, мы будем понимать произвольный разрез Р(А), s А, t V\A с минимальной пропускной способностью.
Теорема (Форд и Фалкерсон). Величина каждого потока из s в t не превосходит пропускной способности мин. разреза, разделяющего s и t, причем существует поток, достигающий этого значения.
Все известные алгоритмы построения максимального потока основываются на последоват. увеличении потока, причем модификация потока, увелич. его величину, чаще всего опирается на метод увеличивающих цепей.
Будем говорить, что дуга е сети S является допустимой дугой из u в v относительно потока f, если
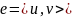 и
и
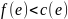 (1) или
(1) или
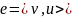 и
и
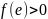 (2).
(2).
В
зависимости от того, какое из приведенных
условий вып., будем
говорить соответственно о согласованной
или несогласованной допустимой дуге
из и в v. Увеличивающей
цепью (длины l) для
данного потока f из s в t
называется произвольная знакоперем.
последовательность (попарно различных)
вершин и дуг
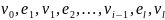 такая, что v0
= s, vl
= t, и для каждого i
l дуга
такая, что v0
= s, vl
= t, и для каждого i
l дуга
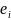 допустима из vi–1
в vi
относительно потока f.
допустима из vi–1
в vi
относительно потока f.
42. Знаковые орграфы и задачи социологии. Теорема Харари о балансе. Недостатки математической модели о балансе.
Знаковый граф — граф, каждому ребру кот. приписан какой-либо знак.
Знак маршрута определяется как знак произведения входящих в них дуг или ребер (если знак плюс зам. на +1, а знак минус на –1).
Маршрут имеет знак минус, если число дуг / ребер в нем нечетно, иначе — плюс.
Хейдер изучал задачи из обл. социологии малых групп людей.
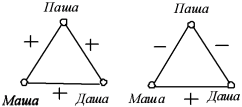
#: группа из 3 человек. Знак означает явно выраженную симпатию или антипатию.
![]()
Малая группа является сбалансированной тогда и только тогда, когда представляющий ее знаковый граф сбалансирован.
Теорема Харари о балансе.
Для знакового графа G=(V,E) следующие утверждения эквивалентны:
Граф G сбалансирован.
Каждая замкнутая цепь в G положительна.
∀ 2 цепи между ∀ 2 вершинами имеют одинаковый знак.
Критерий баланса. Множество вершин можно разбить на два подмножества так, что каждое положительное ребро соединяет вершины одного подмножества и каждое отрицательное соединяет вершины различ. подмножеств.
Недостатки математической модели о балансе:
Предположение о «симметрии симпатий» (в 2 стороны, если граф ненаправленный).
Игнорируется «сила» симпатий.
Не разделяются типы несбалансированности.
Нет градаций степени сбалансированности.
43. Процедура математического моделирования. Модель когнитивных карт. Принцип построения когнитивной карты. Контуры положительной и отрицательной обратной связи. Устойчивость / изменчивость моделей на знаковых орграфах.
Процедура математического моделирования:
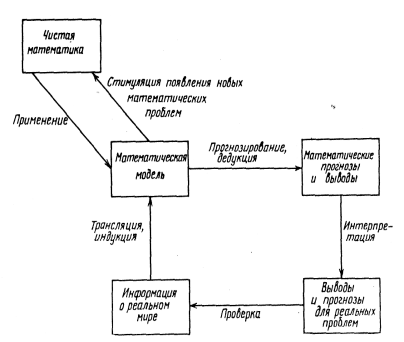
Когнитивная карта — причинно-следственная сеть связей в наборе факторов (концептов), в виде которых предства. информация о системе.
Построение когнитивной карты моделируемой системы означает снятие неопределенности с ее структуры путем формирования модели знаний об этой системе.
В основе когнитивной карты лежат знаковые орграфы.
Принцип построения когнитивной карты.
При составлении когнитивной матрицы эксперту потребуется все время отвечать на вопросы:
1) Какой концепт явл. причиной, а какой следствием?
2) Какое действие на один концепт окажет усиление другого концепта (усиление / ослабление)?
3) В какой степени ослабится или усилится концепт? "Усиление–ослабление " носит абстрактный характер, и эксперту необходимо проставить веса у дуг (проинтерпретир. релевантную причинно–следств. связь).
Т. о. эксперт определяет наиб. важные, непосредств. связи между концептами (связи, кот. существуют в представлении экспертов в «явном» виде).
Контуры положит. и отриц. обратной связи.:
Контуры в знаковом орграфе соответствуют контурам обратной связи; контуры, усил. отклонение — контурам положит. обратной связи, а контуры, противодейств. отклонению — контурам отриц. обратной связи.
Контур, усил. отклонение — контур, в кот. увеличение (уменьшение) любой переменной приводит к ее последующему увеличению (уменьшению).
Контур, противодейств. отклонению — контур, в кот. увеличение любой переменной приводит (через другие переменные контура) к ее уменьшению и наоборот.
Неустойчивость системы — когда в ней много контуров, усил. отклонение.
Устойчивость системы проверяется математически:
1) Строится весовая матрица смеж. A (веса = +1 или -1).
2)
Находятся все собственные значения λ
матрицы A:
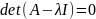 ,
где I — единич.
матрица.
,
где I — единич.
матрица.
3)
Если все собств. знач.
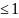 ,
то система устойчива.
,
то система устойчива.
44. Сети Петри. Аналитическое задание. Функционирование сети Петри. Конечные разметки сети. Основные свойства сети Петри: К-ограниченность, безопасность, сохраняемость, достижимость, покрываемость, живость.
Сеть Петри определяется как двудольный граф. Т.е. все вершины графа относятся к одному из двух классов — позициям (местам) и переходам.
Позиции изображаются окружностями, переходы — направленными дугами. Каждая дуга связывает вершины только разных классов.
Аналитическое задание.:
Сеть
Петри — набор
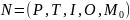 ,
где P — множ. вершин, T — множ. переходов,
I:T®P*
— соответствие между множ. переходов
и вершин, задающее входные позиции
каждого перехода. О:T®P*
— соответствие между множеством
переходов и вершин, задающее выходные
позиции каждого перехода, M0 –
начальная разметка сети.
,
где P — множ. вершин, T — множ. переходов,
I:T®P*
— соответствие между множ. переходов
и вершин, задающее входные позиции
каждого перехода. О:T®P*
— соответствие между множеством
переходов и вершин, задающее выходные
позиции каждого перехода, M0 –
начальная разметка сети.
Разметку сети до срабатывания любого перехода называют начальной разметкой. Затем срабатывает какой-либо переход и разметка сети меняется. После этого изменения какой-либо переход может перестать срабатывать или наоборот.
Последовательное срабатывание переходов и соответствующее изменение разметки сети называют процессом функционирования сети.
Разметку сети при завершении процесса срабатывания называют конечной разметкой.
Функционирование сети Петри описывается формально с помощью множ. последовательностей срабатываний и множ. достижимых в сети разметок.
Конечные разметки сети.:
Одна из основных проблем в теории сетей Петри — это задача о конечности функционирования сети (т.е. о достижении тупиковой разметки, «смертельные объятия»). Тупиковая разметка — разметка, при которой ни один переход не может сработать.
Основные свойства:
K-oграниченность — число меток в любой позиции сети не может превысить некоторого значения K.
Позиция р называется безопасной, если для любой разметки сети M количество фишек M(p) £ 1; сеть безопасна, если все ее позиции безопасны. Любая достижимая в безопасной сети разметка представляет собой вектор из 0 и 1.
Сохраняемость — св-во сети, хар-зующее невозмож. возник. или уничтож. ресурсов в моделир. объекте.
Разметка М достижима в сети Петри, если существует цепочка срабатываний переходов, ведущая из начального состояния в М.
Разметка М'=(P1'...Pn') покрывает состояние М”=(P1"...Pn"), если для каждого i=1, ...,n имеет место Pi' ≥ Pi", т.е. имеет место М' ≥ М”.
Живость — свойство сети, означающее, что из любого состояния, достижимого из начального, возможен переход в любое другое достижимое состояние.
