48. Основные схемы логически правильных рассуждений.
Наряду с алфавитом и правилами построения сложных высказываний (логических формул), языки логики высказываний содержат правила преобразования логических формул.
Правила преобразования реализуют общелогические законы и обеспечивают логически правильные рассуждения. Корректность допустимых в логике преобразований является фундаментальным свойством формальной (математической) логики.
Процесс получения новых знаний, выраженных высказываниями, из других знаний, также выраженных высказываниями, называется рассуждением (умозаключением).
Исходные высказывания называются посылками (гипотезами, условиями), а получаемые высказывания — заключением (следствием).
Д
ля
построения логических формул, отражающих
логически правильные рассуждения,
следует все посылки соединить конъюнкцией
& и полученную таким
образом обобщенную посылку связать
импликацией ®
с выводом: ((A®B)&A)®B.
П
равило
заключ. — утвержд. модус:
Правило отрицания — отриц. модус:
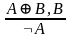
Правило утв.–отриц.:
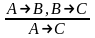
Правило транзитивности:
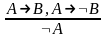
Закон противоречия:
Правило контрапозиции:
Сведение к абсурду:
49. Алгебра логики. Бинарные логические операции. Существенные и несущественные (фиктивные) переменные. Функционально полные системы (базисы). Булева алгебра логики. Законы булевой алгебры. Примеры других алгебр логики.
Матем. логика: логика высказ. и логика предикатов.
Логика высказываний может быть представ. 2-мя подходами: алгеброй логики (высказываний) и исчислением высказываний.
Алгебра логики — алгебра, образованная множ. B={0,1} вместе со всеми возможными операциями на нем.
Алгебра логики как раздел математической логики изучает строение сложных логических высказываний (логических формул) и способы установления их истинности с помощью алгебраических методов.
Переменная xi в функции f(x1,…, xi–1, xi, xi+1, …, xn) называется несущественной (фиктивной), если f(x1,…, xi–1, 1, xi+1, …, xn) = f(x1,…, xi–1, 0, xi+1, …, xn) при любых значениях остальных переменных. В противном случае — существенная переменная.
Функционально полные системы (базисы) — наборы логических операций, с помощью которых можно выразить любые другие логические операции.
Теорема: Всякая логическая функция может быть представлена булевой формулой, т.е. как суперпозиция дизъюнкции, конъюнкции и отрицания.
Алгебра (Р2; &, Ú, Ø), основным множеством которой является множество всех логических функций Р2, а операциями дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй логических операций. Является наиболее изученной. Формулы, содержащие кроме переменных и скобок знаки этих функций называются булевыми.
Законы булевой алгебры:
1) ассоц.: aÚ(bÚc)=(aÚb)Úc, aÙ(bÙc)=(aÙb)Ùc;
2) коммут.: aÚb=bÚa, aÙb=bÙa;
3) дистр.: aÙ(bÚc)=(aÙb)Ú(aÙc); aÚ(bÙc)=(aÚb)Ù(aÚc);
4) иденп.: aÚa=a; aÙa=a;
5) инвол. (двойного отрицания) ØØa=a;
6) св-ва 0: aÚ0=a, aÙ0=0;
7) св-ва 1: aÚ1=1, aÙ1=a.
8) де-Моргана: ØaÚØb=Ø(aÙb), ØaÙØb=Ø(aÚb);
9) св-ва дополнения: aÙØа=0; aÚØа=1;
10) поглощения aÚaÙb=a, aÙ(aÚb)=a;
11) склеивания aÙb Ú aÙØb =a, (aÚb)Ù(aÚØb)=a;
12) обобщенное склеивание aÙc Ú bÙØc Ú aÙb = aÙc Ú bÙØc;
13) a Ú ØaÙb = aÚb
# алгебр логик (функционально полных базисов):
1){&, Ú,1}
2){o} (Функция Вебба),
3){½} (штрих Шеффера);
4){®, 0}, { ¬, 1},
и др.
50. Суперпозиция булевых функций и ее формула. Глубина формулы. Таблицы истинности для сложных формул. Эквивалентность формул. Тождественно истинная, тождественно ложная и выполнимая функция. Единичный и нулевой набор функции.
Суперпозицией F булевых функций f0 и f1,...,fm называется функция F=f0(g1(x1,...,xm),...,gn(x1,...,xm)), где каждая из функций gi(x1, ...,xm) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f1,...,fm.
Формулой называется выражение, описывающее эту суперпозицию.
Символы переменных, а также функции const_0 и const_1 считаются формулами глубины 0.
Глубина формулы:
Определить глубину формулы F= ((А→В)&C) ÚA.
1) Вначале выполняется f1= А→В. Глубина которой k1=max(0,0)+1=1
2) Следующей будет выполняться функция f2=f1&C. Функция f2 имеет глубину k2=max(k1,0)+1=max(1,0)+1=2
3) Далее выполнятся функция f3=f2ÚA, глубина которой k3=max(k2,0)+1=max(2,0)+1=3
Таким образом, глубина исходной формулы равна 3.
Таблицы истинности для сложных функций строится поэтапно, путем выделения простых функций согласно последовательности их выполнения.
#: Таблица истинности для формулы F= ((А→В)&C)ÚA:
A |
B |
C |
A→B |
f1&C |
f2ÚA |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Формулы (высказывания) явл. эквивалентными (равносильными), если для всех наборов переменных совпадают их значения.
Формула называется тождественно истинной (общезначимой, тавтологией), если при всех возможных наборах переменных формула равна 1
Формула называется тождественно ложной (противоречием), если при всех возможных наборах переменных формула равна 0.
Формула называется выполнимой, если при некоторых наборах переменных формула равна 1.
Единичным набором переменных называется набор переменных, при которых функция равна 1. Множество единичных наборов называется единичным множеством.
Нулевым набором переменных называется набор переменных, при которых функция равна 0. Множество нулевых наборов называется нулевым множеством.