56. Функции k-значной логики и их задание с помощью таблицы истинности и таблицы Кэли. Примеры k-значных логик: алгебра Вебба, алгебра Поста, алгебра Россера-Тьюкетта.
___Функция , отображающая n-мерный k-значный кортеж
в множество {0, 1, ..., k – 1}, называется функцией k-значной логики.
___Будем задавать функцию k-значной логики с помощью таблицы истинности (одномерной таблицы), число строк которой равно kn, или двумерной таблицы, число клеток которой равно k2.
АЛГЕБРА ВЕББА::::
Конечнозначная функция Вебба
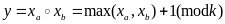
Конечнозначная алгебра Вебба
А
ЛГЕБРА
ПОСТА:::::
где дизъюнкция
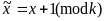
Цикл
__В случае k=2, цикл и дизъюнкция соответствуют булевым операциям.
АЛГЕБРА РОССЕРА_ТЬЮКЕТТА::
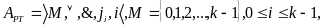
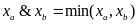
__Конъюнкция
_
_характеристические
функции:
57. Формальные теории. Принципы построения формальной теории. Задание Исчисления Высказывания как формальной теории. Выводимость формул, разрешимые и неразрешимые формулы. Свойства Исчисления Высказываний: полнота, непротиворечивость и разрешимость.
Формальная теория считается определенной, если выполнены следующие условия:
Задано некоторое счетное множество символов — алфавит теории T.
Определено подмножество правильно построенных последовательностей символов теории T, называемых формулами теории T (язык теории).
Выделено некоторое множество формул, называемых аксиомами теории T;
Задано конечное множество R1, R2, ..., Rn отношений между формулами, называемых правилами вывода.
Задание Исчисления Высказывания как формальной теории.
Алфавит исчисления высказываний состоит из переменных высказываний (пропозициональных букв): A, B, C …, знаков логических связок Ú, &, Ø, ® и скобок (, ).
Формулы:
а) переменное высказывание (пропозициональная буква) есть формула;
б) если A и B — формулы, то (A ÚB), (A &B), (A ®B) и (ØA) также формулы;
в) выражение является формулой тогда и только тогда, когда это может быть установлено с помощью пп. а) и б)
Существует несколько систем аксиом исчисления высказываний.
Выводимость формул:
Если формулы F1, …, Fn, G находятся в отношении R, то формула G называется непосредственно выводимой из F1, …, Fn по правилу R. формулы F1, …, Fn, называются посылками правила R, а G — его следствием или заключением.
Выводом в T формулы G из формул A1, …, An, называется всякая последовательность F1, F2, ..., Fm формул такая, что Fm = G, а для любого i формула Fi есть либо аксиома теории T, либо одна из исходных формул A1, …, An, либо выводима из формул F1, …, Fi-1 по одному из правил вывода.
Если существует вывод G из A1, …, An, то говорят, что G выводима из A1, …, An т.е. является теоремой формальной теории Т. Этот факт обозначается A1, …, An |— G.
Формулы A1, …, An называются гипотезами или посылками вывода. Переход в выводе от Fi-1 к Fi называется i-м шагом вывода.
РАЗРЕШИМЫЕ И НЕРАЗ, ФОРМУЛЫ:::
В общем случае может не существовать эффективной процедуры, с помощью которой можно определить по данной формуле, существует ли ее вывод в теории T.
Формула, для которой такая процедура существует, называется разрешимой в этой теории, в противном случае — неразрешимой.
Иначе говоря, для неразрешимых формул нельзя построить алгоритм, который ответит на вопрос: является ли формула теоремой.
СВ_ВА ИСЧИСЛ, ВЫСКАЗ,,
ПОЛНОТА::::::
Полнота. Имеют место следующие метатеоремы.
Теорема 1: Всякая теорема исчисления высказываний (Т) есть тавтология (т.е. тождественно истинная формула)
Теорема 2: Всякая тавтология является теоремой исчисления высказываний.
Таким образом, теоремами теории Т являются тождественно истинные формулы и только они.
Формальная теория Т (исчисление высказываний) является полной теорией
НЕПРОТИВОРЕЧИВОСТЬ:::::
Непротиворечивость: в теории Т нет одновременной
выводимости теоремы и ее отрицания.
Из теоремы 1 следует, что теория Т непротиворечива.
РАЗРЕШИМОСТЬ::::
Теория Т разрешима как формальная теория.
Алгоритм, который определяет для любой формулы
теории, является ли эта формула теоремой теории,
может состоять в вычислении истинностных значений
формулы в каждой интерпретации. Принципиально это
выполнимо за конечное время в силу конечности числа
интерпретаций и числа операций, присутствующих в
формуле.
58. Предикат: n-местный (n=0, n>0). Предикатные формулы. Связь между предикатами, отношениями и функциями. Модель в логике предикатов.
1) Под 0-местным предикатом понимается произвольное высказывание.
2) Элементарной формулой называется всякая пропозициональная переменная, а также любая m-местная предикатная переменная (m > 0) .
__Из элементарных формул строятся предикатные формулы:
1) Все элементарные формулы суть формулы;
2) Если А и В — формулы, то выражения (А & В), (А Ú В), (А ® В), (А ~ В), ØА считаются формулами;
3) если А — формула, x — предметная переменная, то "x А и $x В суть формулы.
Виды математических предикатов:
__Предикат тождества E(x1,x2): N2 ® B: E(a1, a2) = 1 тогда и только тогда, когда a1 = a2, xi ÎN
__Предикат порядка Q (x1,x2) : N2 ® B: Q(a1, a2) = 1 тогда и только тогда, когда a1 £ a2, xi ÎN
__Предикат делимости D (x1,x2) : N2 ® B: D(a1, a2) = 1 тогда и только тогда, когда a1 делится на a2, xi ÎN
__Предикат суммы S (x1,x2,x3) : N3 ® B: S(a1, a2, a3) = 1 тогда и только тогда, когда a1 + a2 = a3, xi ÎN
__Предикат произведения P (x1,x2,x3) : N3 ® B: P(a1, a2, a3) = 1 тогда и только тогда, когда a1 * a2 = a3, xi ÎN
СВЯЗЬ МЕЖДУ ПРЕДИКАТАМИ,ОТНОШЕНИЯМИ И ФУНКЦИЯМИ:
____Всякой n-местной функции f(x1, …,xn), f:M1 ´ M2 ´…´ Mn® M соответствует n+1 - местный предикат P(x1, …,xn,xn+1), P: M1 ´ M2 ´…´ Mn+1 ® B, такой, что P(a1, …,an, an+1) = 1, если и только если f(a1, …,an) = an+1.
____Понятие предиката шире понятия функции, поэтому обратное соответствие (от (n + 1)-местного предиката к n-местной функции) возможно не всегда, а только для таких предикатов P¢ для которых выполняется условие:
если P¢(a1, …,an, an+1) = 1, то для любого
a¢n+1 ¹ an+1 P¢(a1, …,an, a¢n+1) = 0.
МОДЕЛЬ В ЛОГИКЕ ПРЕДИКАТОВ:::
__Моделью M в логике предикатов называется множество М вместе с заданной на нем совокупностью предикатов S={P1, …, Pk} : M = (М; P1, …, Pk),
где М — основное множество модели M ;
S={P1, …, Pk} — сигнатура модели M .
___Аналогично предыдущему определяются формулы, выполнимые на модели M, тождественно-истинные и тождественно-ложные на модели M.