38. Алгоритм нахождения кратчайшего расстояния от источника до всех верши в случае бесконтурных графов. Сложность алгоритма.

Предполагается, что каждая дуга идет из вершины с меньшим номером в вершину с большим номером.

Данные: ориентированный граф <V, E>, где для произвольной дуги имеем . Этот граф определен списками ПРЕДШ[v], v Î V.

Результаты: Расстояния от v₁ до всех вершин графа: D[v_i] = d(v₁, v_i), i = 1, ..., n.

Сложность алгоритма порядка O(m), т. к. каждая дуга анализируется (стр. 6) в точности 1 раз.

Алгоритм:

• Выбир. вершина-источник.

• Вып. первонач. оценка кратчайших расстояний.

• Вып. оценка расстояний ч/з верш., предшеств. текущей — выбир. мин. между найденным расстоянием до текущей и расстоянием до нее ч/з предшествующие.

Begin

D[vs] := 0; // выбор источника

for j := 2 to n do D[vj] := ¥; первоначальная оценка

for j := 2 to n do // цикл по всем вершинам

for vi Î ПРЕДШ [vj] // вершины, предшествующие текущей

do D[vj] := min(D[vj], D[vi] + A[vi, vj]); // оценка расстояния через предшествующие

End

39. Система pert. Алгоритм топологической сортировки. Критический путь и способ его нахождения.

Бесконтурные орграфы исп-ся в качестве моделей ситуаций, когда задачи должны вып. в опред. порядке.

В задаче о планировании заданий соответствующий бесконтурный граф имеет название «система PERT».

Предположим, что необходимо определить порядок, в котором следует изучать предметы, учитывая их зависимость друг от друга. Это позволяет сделать алгоритм топологической сортировки (по сути аналогич. алгоритму перенумерации вершин).

Алгоритм генерир. послед-ть согласованных меток для вершин бесконтурного графа таким образом, что каждая дуга будет иметь вид , где . В начале работы алгоритма значение A(v) равно кол-ву дуг входящих в данную вершину // аналог ЧЗАХ

Алгоритмы находят применения в методах PERT или CPM. Эти методы основываются на построении графа (сети PERT или сети CPM), дуги кот. соответствуют элементарным задачам, составляющим проект, а их веса указывают на время, необходимое для решения отдельных задач.

Кроме этого, предполагается, что для произвольных дуг этого графа задача, изображаемая одной дугой, должна быть закончена перед началом решения задачи, изображаемой др. дугой.

Критический путь и способ его нахождения.

Графы сети PERT и CPM бесконтурные.

Задача: найти самый длинный путь из источника (начало проекта), до конечной вершины (окончание проекта).

Такой путь называется критическим путем. Длина пути определяет время, необходимое для реализации всего проекта. Очевидно, что задача сводится к задаче о кратчайшем пути, если измененить знак каждого веса a(u, v) на обратный.

Существует несколько способов нахождения критического путя. Например, алгоритм Флойда ( ) и алгоритм Форда–Беллмана .

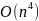40. Алгоритм Флойда — кратчайшее расстояние между всеми парами вершин. Обоснование. Сложность алгоритма. Транзитивное замыкание. Алгоритм Уоршала — нахождение транзитивного замыкания. Обоснование алгоритма Уоршала и его временная сложность.

Определить расстояния между всеми парами вершин можно, используя n раз один из рассм. методов нахождения расстояний от фиксир. вершины. В общем случае — алгоритм Форда–Беллмана со сложностью .

Однако, у алгоритма Флойда сложность .

Рассмотрим орграф G = <V, E>, где V = {v₁, ..., v_n}, и предположим, что A = [a_ij] есть матрица весов (a_ij = a(v_i, v_j)). Обозначив через d_ij^(m) длину кратчайшего пути из v_i  в v_j, содержащего не более m дуг, получаем следующие очевидные уравнения:

; .

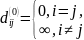Обоснование алгоритма Флойда.

Пусть задан граф, содерж. m+1 вершину. Рассм. кратчайший путь из v_i в v_j, содерж. вершин .

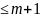1. Если этот путь не содержит 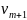, то .

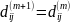11. Если же он содерж. , то, деля путь на отрезки от v_i до v_m и от v_m до v_j, получ. рав-во .

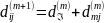Тогда рекуррентная формула для задания расстояния между всеми парами вершин из множества {v₁, ..., v_m, v_m+1} имеет вид:

; .

Из 2 возмож. знач. длины выбир. мин.

Данные: матрица весов дуг A[i, j], 1 £ i, j £ n, орграфа без контуров отрицательной длины.

Результаты: расстояния между всеми парами вершин D[i, j] = d(vi, vj).

1. Begin

2. for i := 1 to n do

3. for j := 1 to n do D[i, j] := A[i, j];

4. for i := 1 to n do D[i, i] := 0;

5. for m := 1 to n do

6. for i := 1 to n do

7. for j := 1 to n do

8. D[i, j] := min(D[i, j], D[i, m] + D[m, j];

9. End;

Сложность алгоритма — O(n³). Такую же сложность имел алгоритм Форда–Беллмана нахождения расстояний от фиксированной вершины до всех остальных вершин.

С задачей опред. кратчайших путей в графе тесно связана задача транзитив. замыкания бинарного отношения.

Транзитивное, если квадрат отношения явл. подмнож. исх. отнош.: ( ).

Бинарное отношение E Í V´ V можно однозначно представить орграфом G = <V, E>. Для произвольного отношения E определяется отношение E*, такое что E*={(x, y): в <V, E> сущ. путь ненул. длины из x в y}.

E* — транзитивное отношение на множестве V и E Í E*. E* является наименьшим транзитивным замыканием, содержащим E.

Обоснование алгоритма Уоршалла:

Строка ; зам. на .

Если в отношении присутствуют обе пары (i,m) и (m,j), то в транзитивном замыкании должна существовать пара (i,j). Т.е. .

Сложность алгоритма O(n³).